FastLRNR and Sparse Physics Informed Backpropagation

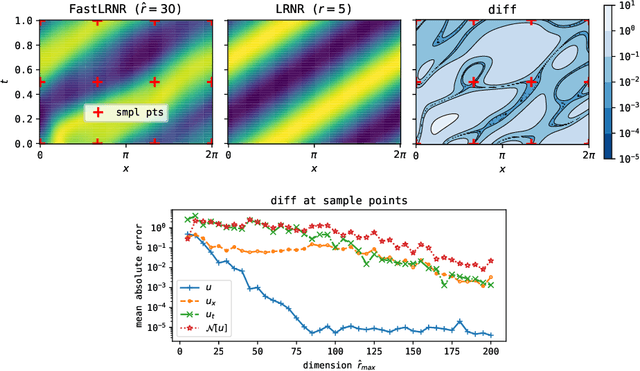
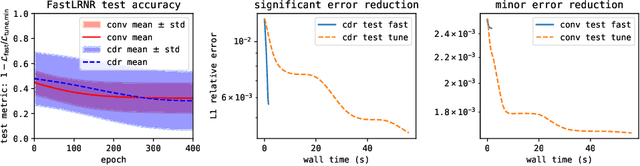
We introduce Sparse Physics Informed Backpropagation (SPInProp), a new class of methods for accelerating backpropagation for a specialized neural network architecture called Low Rank Neural Representation (LRNR). The approach exploits the low rank structure within LRNR and constructs a reduced neural network approximation that is much smaller in size. We call the smaller network FastLRNR. We show that backpropagation of FastLRNR can be substituted for that of LRNR, enabling a significant reduction in complexity. We apply SPInProp to a physics informed neural networks framework and demonstrate how the solution of parametrized partial differential equations is accelerated.

On the performance of sequential Bayesian update for database of diverse tsunami scenarios

Although the sequential tsunami scenario detection framework was validated in our previous work, several tasks remain to be resolved from a practical point of view. This study aims to evaluate the performance of the previous tsunami scenario detection framework using a diverse database consisting of complex fault rupture patterns with heterogeneous slip distributions. Specifically, we compare the effectiveness of scenario superposition to that of the previous most likely scenario detection method. Additionally, how the length of the observation time window influences the accuracy of both methods is analyzed. We utilize an existing database comprising 1771 tsunami scenarios targeting the city Westport (WA, U.S.), which includes synthetic wave height records and inundation distributions as the result of fault rupture in the Cascadia subduction zone. The heterogeneous patterns of slips used in the database increase the diversity of the scenarios and thus make it a proper database for evaluating the performance of scenario superposition. To assess the performance, we consider various observation time windows shorter than 15 minutes and divide the database into five testing and learning sets. The evaluation accuracy of the maximum offshore wave, inundation depth, and its distribution is analyzed to examine the advantages of the scenario superposition method over the previous method. We introduce the dynamic time warping (DTW) method as an additional benchmark and compare its results to that of the Bayesian scenario detection method.

A Low Rank Neural Representation of Entropy Solutions

We construct a new representation of entropy solutions to nonlinear scalar conservation laws with a smooth convex flux function in a single spatial dimension. The representation is a generalization of the method of characteristics and posseses a compositional form. While it is a nonlinear representation, the embedded dynamics of the solution in the time variable is linear. This representation is then discretized as a manifold of implicit neural representations where the feedforward neural network architecture has a low rank structure. Finally, we show that the low rank neural representation with a fixed number of layers and a small number of coefficients can approximate any entropy solution regardless of the complexity of the shock topology, while retaining the linearity of the embedded dynamics.

Hypernetwork-based Meta-Learning for Low-Rank Physics-Informed Neural Networks

In various engineering and applied science applications, repetitive numerical simulations of partial differential equations (PDEs) for varying input parameters are often required (e.g., aircraft shape optimization over many design parameters) and solvers are required to perform rapid execution. In this study, we suggest a path that potentially opens up a possibility for physics-informed neural networks (PINNs), emerging deep-learning-based solvers, to be considered as one such solver. Although PINNs have pioneered a proper integration of deep-learning and scientific computing, they require repetitive time-consuming training of neural networks, which is not suitable for many-query scenarios. To address this issue, we propose a lightweight low-rank PINNs containing only hundreds of model parameters and an associated hypernetwork-based meta-learning algorithm, which allows efficient approximation of solutions of PDEs for varying ranges of PDE input parameters. Moreover, we show that the proposed method is effective in overcoming a challenging issue, known as "failure modes" of PINNs.

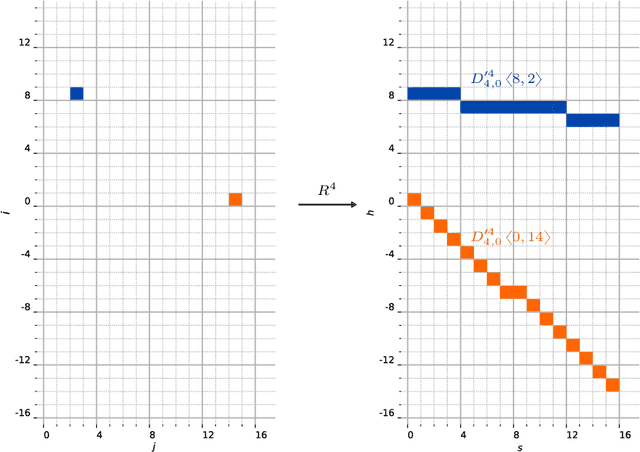
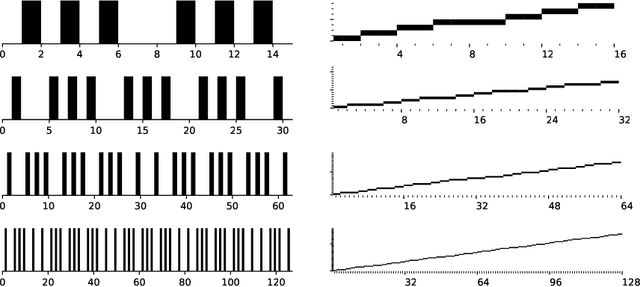
A range characterization of the single-quadrant ADRT

This work characterizes the range of the single-quadrant approximate discrete Radon transform (ADRT) of square images. The characterization is given in the form of linear constraints that ensure the exact and fast inversion formula [Rim, Appl. Math. Lett. 102 106159, 2020] yields a square image in a stable manner. The range characterization is obtained by first showing that the transform is a bijection between images supported on infinite half-strips, then identifying the linear subspaces that stay finitely supported under the inversion formula.

Depth separation for reduced deep networks in nonlinear model reduction: Distilling shock waves in nonlinear hyperbolic problems

Classical reduced models are low-rank approximations using a fixed basis designed to achieve dimensionality reduction of large-scale systems. In this work, we introduce reduced deep networks, a generalization of classical reduced models formulated as deep neural networks. We prove depth separation results showing that reduced deep networks approximate solutions of parametrized hyperbolic partial differential equations with approximation error $\epsilon$ with $\mathcal{O}(|\log(\epsilon)|)$ degrees of freedom, even in the nonlinear setting where solutions exhibit shock waves. We also show that classical reduced models achieve exponentially worse approximation rates by establishing lower bounds on the relevant Kolmogorov $N$-widths.

Exact and Fast Inversion of the Approximate Discrete Radon Transform

We give an exact inversion formula for the approximate discrete Radon transform introduced in [Brady, SIAM J. Comput., 27(1), 107--119] that is of cost $O(N \log N)$ for a square 2D image with N pixels.