A range characterization of the single-quadrant ADRT

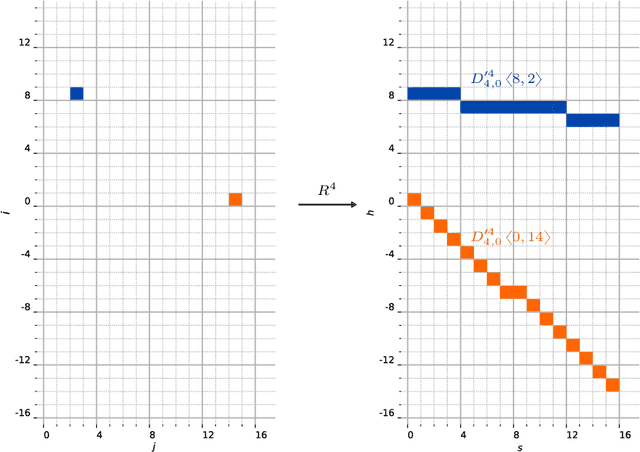
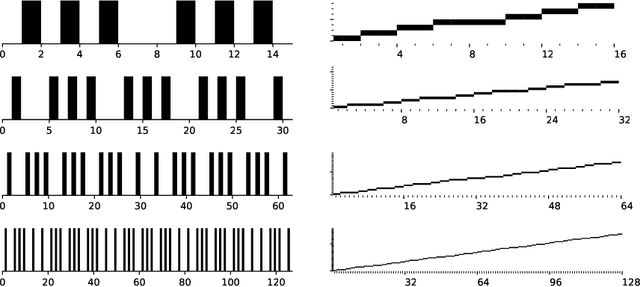
This work characterizes the range of the single-quadrant approximate discrete Radon transform (ADRT) of square images. The characterization is given in the form of linear constraints that ensure the exact and fast inversion formula [Rim, Appl. Math. Lett. 102 106159, 2020] yields a square image in a stable manner. The range characterization is obtained by first showing that the transform is a bijection between images supported on infinite half-strips, then identifying the linear subspaces that stay finitely supported under the inversion formula.