Approximation of functions with one-bit neural networks

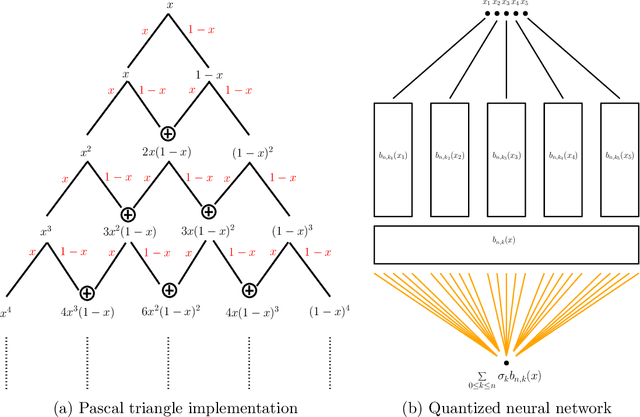
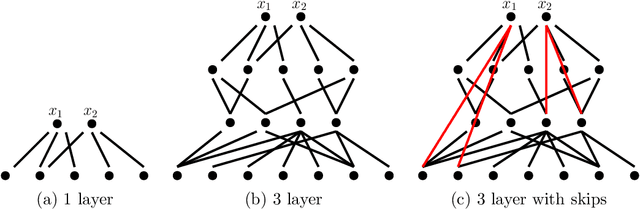
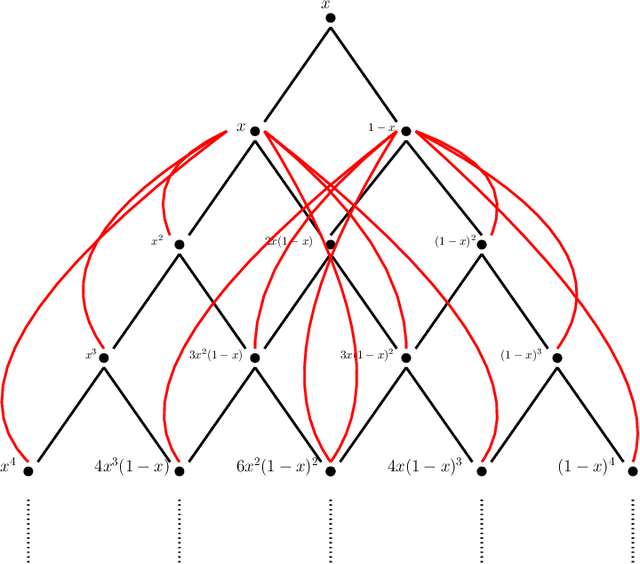
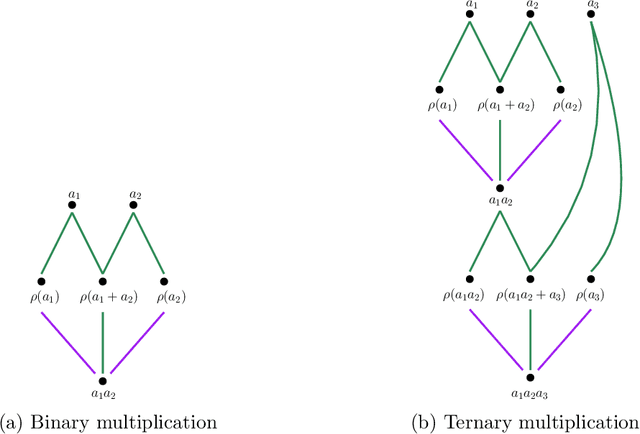
This paper examines the approximation capabilities of coarsely quantized neural networks -- those whose parameters are selected from a small set of allowable values. We show that any smooth multivariate function can be arbitrarily well approximated by an appropriate coarsely quantized neural network and provide a quantitative approximation rate. For the quadratic activation, this can be done with only a one-bit alphabet; for the ReLU activation, we use a three-bit alphabet. The main theorems rely on important properties of Bernstein polynomials. We prove new results on approximation of functions with Bernstein polynomials, noise-shaping quantization on the Bernstein basis, and implementation of the Bernstein polynomials by coarsely quantized neural networks.

Stability and Super-resolution of MUSIC and ESPRIT for Multi-snapshot Spectral Estimation

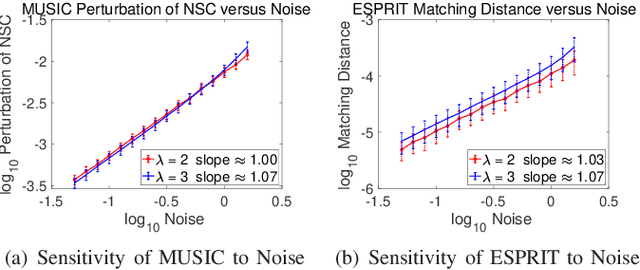
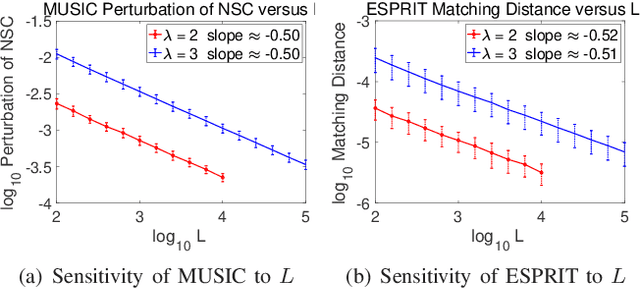
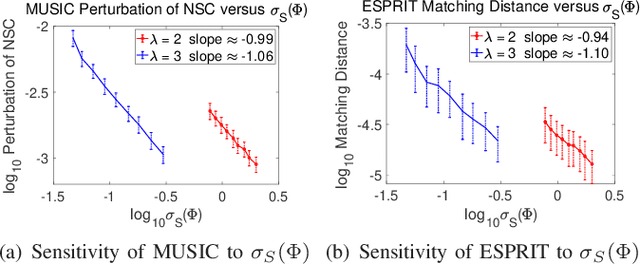
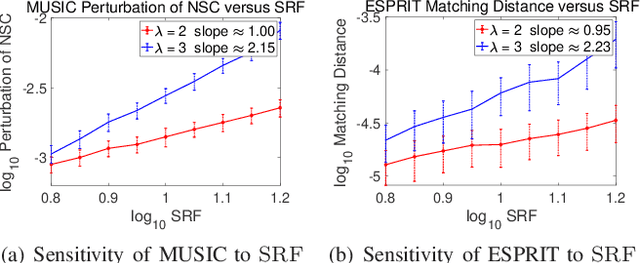
This paper studies the spectral estimation problem of estimating the locations of a fixed number of point sources given multiple snapshots of Fourier measurements collected by a uniform array of sensors. We prove novel non-asymptotic stability bounds for MUSIC and ESPRIT as a function of the noise standard deviation, number of snapshots, source amplitudes, and support. Our most general result is a perturbation bound of the signal space in terms of the minimum singular value of Fourier matrices. When the point sources are located in several separated clumps, we provide an explicit upper bound of the noise-space correlation perturbation error in MUSIC and the support error in ESPRIT in terms of a Super-Resolution Factor (SRF). The upper bound for ESPRIT is then compared with a new Cram\'er-Rao lower bound for the clumps model. As a result, we show that ESPRIT is comparable to that of the optimal unbiased estimator(s) in terms of the dependence on noise, number of snapshots and SRF. As a byproduct of our analysis, we discover several fundamental differences between the single-snapshot and multi-snapshot problems. Our theory is validated by numerical experiments.

Exploring the high dimensional geometry of HSI features

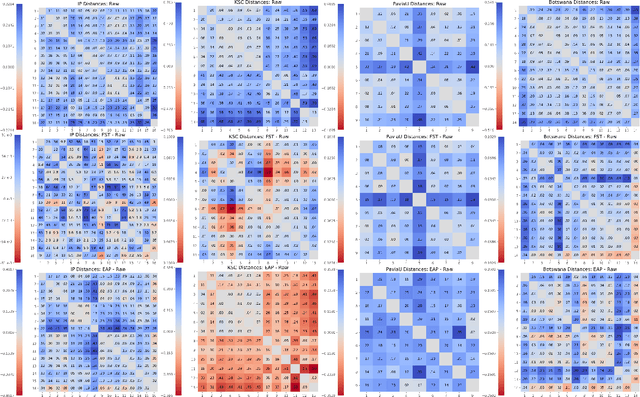
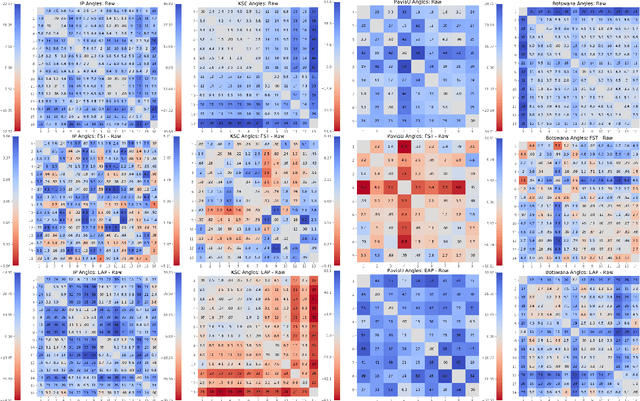
We explore feature space geometries induced by the 3-D Fourier scattering transform and deep neural network with extended attribute profiles on four standard hyperspectral images. We examine the distances and angles of class means, the variability of classes, and their low-dimensional structures. These statistics are compared to that of raw features, and our results provide insight into the vastly different properties of these two methods. We also explore a connection with the newly observed deep learning phenomenon of neural collapse.

Maximal function pooling with applications

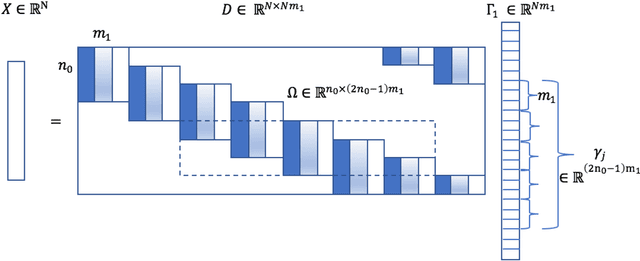
Inspired by the Hardy-Littlewood maximal function, we propose a novel pooling strategy which is called maxfun pooling. It is presented both as a viable alternative to some of the most popular pooling functions, such as max pooling and average pooling, and as a way of interpolating between these two algorithms. We demonstrate the features of maxfun pooling with two applications: first in the context of convolutional sparse coding, and then for image classification.

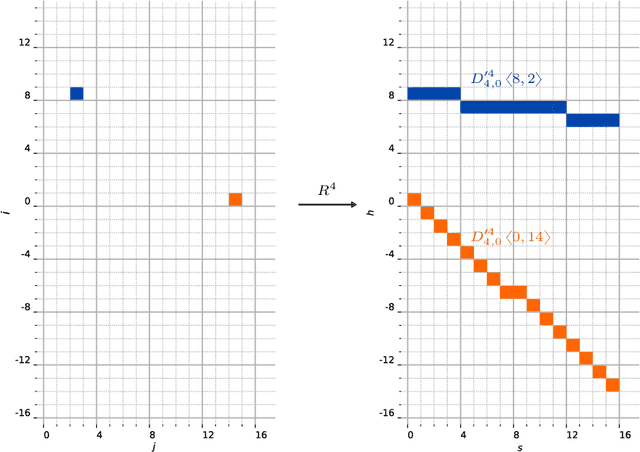
A range characterization of the single-quadrant ADRT

This work characterizes the range of the single-quadrant approximate discrete Radon transform (ADRT) of square images. The characterization is given in the form of linear constraints that ensure the exact and fast inversion formula [Rim, Appl. Math. Lett. 102 106159, 2020] yields a square image in a stable manner. The range characterization is obtained by first showing that the transform is a bijection between images supported on infinite half-strips, then identifying the linear subspaces that stay finitely supported under the inversion formula.

Three-Dimensional Fourier Scattering Transform and Classification of Hyperspectral Images

Recent research has resulted in many new techniques that are able to capture the special properties of hyperspectral data for hyperspectral image analysis, with hyperspectral image classification as one of the most active tasks. Time-frequency methods decompose spectra into multi-spectral bands, while hierarchical methods like neural networks incorporate spatial information across scales and model multiple levels of dependencies between spectral features. The Fourier scattering transform is an amalgamation of time-frequency representations with neural network architectures, both of which have recently been proven to provide significant advances in spectral-spatial classification. We test the proposed three dimensional Fourier scattering method on four standard hyperspectral datasets, and present results that indicate that the Fourier scattering transform is highly effective at representing spectral data when compared with other state-of-the-art spectral-spatial classification methods.