Approximation of functions with one-bit neural networks
Paper and Code
Dec 16, 2021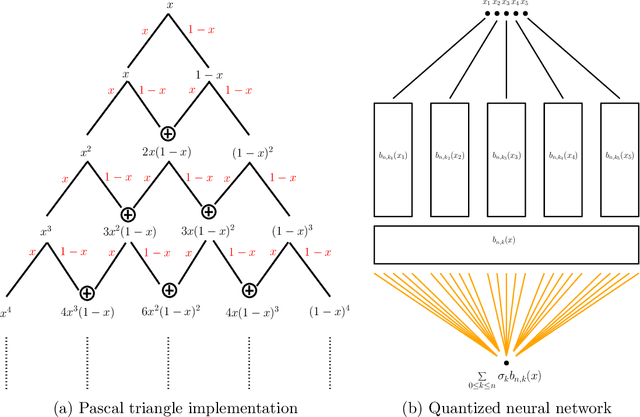
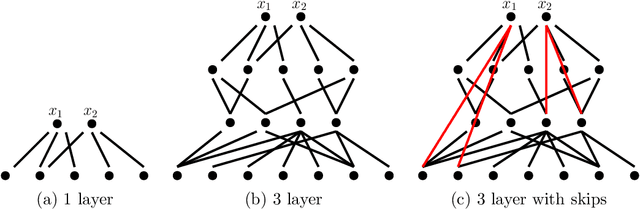
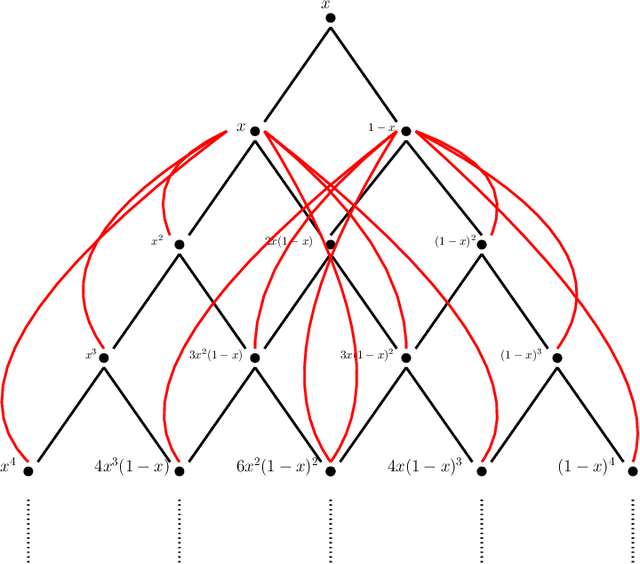
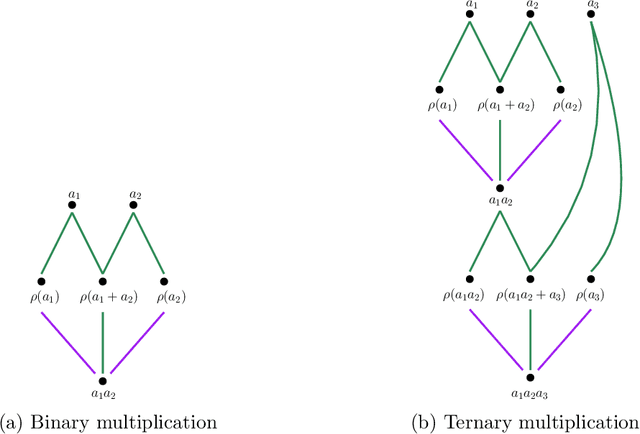
This paper examines the approximation capabilities of coarsely quantized neural networks -- those whose parameters are selected from a small set of allowable values. We show that any smooth multivariate function can be arbitrarily well approximated by an appropriate coarsely quantized neural network and provide a quantitative approximation rate. For the quadratic activation, this can be done with only a one-bit alphabet; for the ReLU activation, we use a three-bit alphabet. The main theorems rely on important properties of Bernstein polynomials. We prove new results on approximation of functions with Bernstein polynomials, noise-shaping quantization on the Bernstein basis, and implementation of the Bernstein polynomials by coarsely quantized neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge