FastLRNR and Sparse Physics Informed Backpropagation

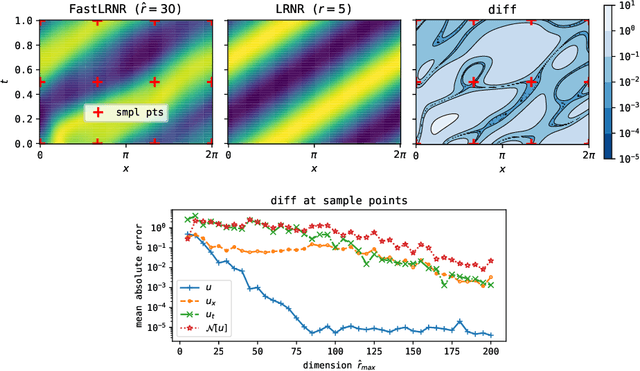
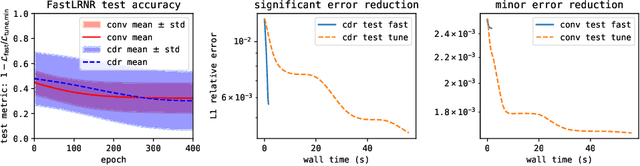
We introduce Sparse Physics Informed Backpropagation (SPInProp), a new class of methods for accelerating backpropagation for a specialized neural network architecture called Low Rank Neural Representation (LRNR). The approach exploits the low rank structure within LRNR and constructs a reduced neural network approximation that is much smaller in size. We call the smaller network FastLRNR. We show that backpropagation of FastLRNR can be substituted for that of LRNR, enabling a significant reduction in complexity. We apply SPInProp to a physics informed neural networks framework and demonstrate how the solution of parametrized partial differential equations is accelerated.

A Low Rank Neural Representation of Entropy Solutions

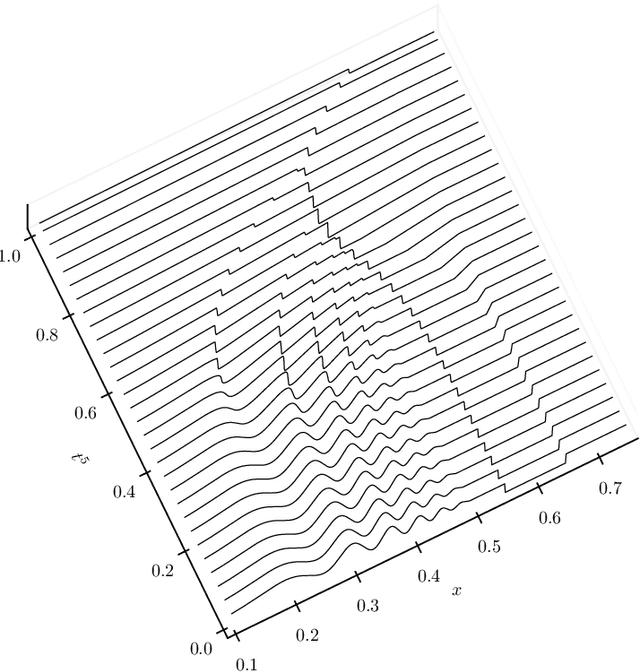
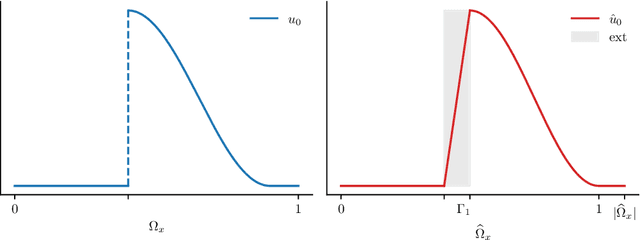
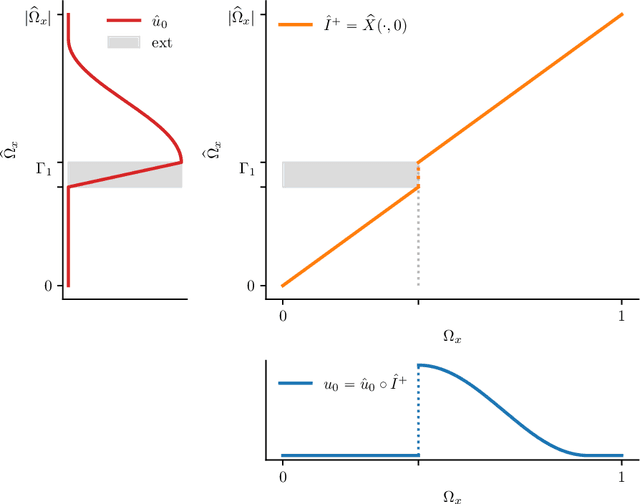
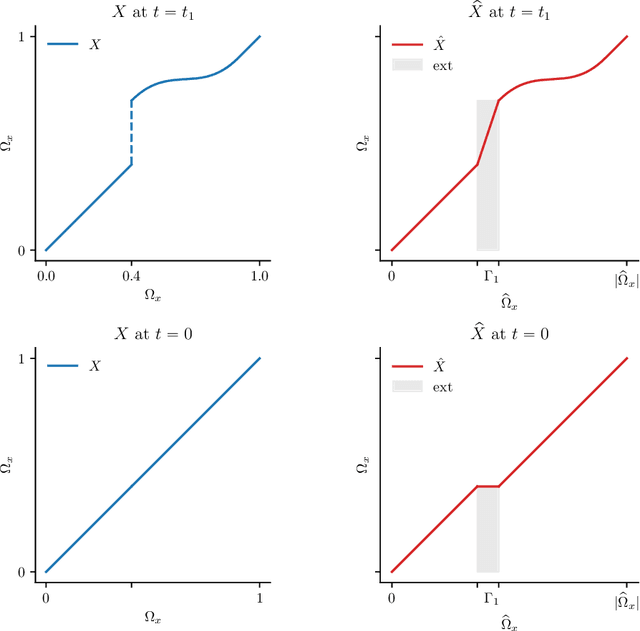
We construct a new representation of entropy solutions to nonlinear scalar conservation laws with a smooth convex flux function in a single spatial dimension. The representation is a generalization of the method of characteristics and posseses a compositional form. While it is a nonlinear representation, the embedded dynamics of the solution in the time variable is linear. This representation is then discretized as a manifold of implicit neural representations where the feedforward neural network architecture has a low rank structure. Finally, we show that the low rank neural representation with a fixed number of layers and a small number of coefficients can approximate any entropy solution regardless of the complexity of the shock topology, while retaining the linearity of the embedded dynamics.