HINTS: Extraction of Human Insights from Time-Series Without External Sources

Human decision-making, emotions, and collective psychology are complex factors that shape the temporal dynamics observed in financial and economic systems. Many recent time series forecasting models leverage external sources (e.g., news and social media) to capture human factors, but these approaches incur high data dependency costs in terms of financial, computational, and practical implications. In this study, we propose HINTS, a self-supervised learning framework that extracts these latent factors endogenously from time series residuals without external data. HINTS leverages the Friedkin-Johnsen (FJ) opinion dynamics model as a structural inductive bias to model evolving social influence, memory, and bias patterns. The extracted human factors are integrated into a state-of-the-art backbone model as an attention map. Experimental results using nine real-world and benchmark datasets demonstrate that HINTS consistently improves forecasting accuracy. Furthermore, multiple case studies and ablation studies validate the interpretability of HINTS, demonstrating strong semantic alignment between the extracted factors and real-world events, demonstrating the practical utility of HINTS.

How Many Experts Are Enough? Towards Optimal Semantic Specialization for Mixture-of-Experts

Finding the optimal configuration of Sparse Mixture-ofExperts (SMoE) that maximizes semantic differentiation among experts is essential for exploiting the full potential of MoE architectures. However, existing SMoE frameworks either heavily rely on hyperparameter tuning or overlook the importance of diversifying semantic roles across experts when adapting the expert pool size. We propose Mixture-of-Experts for Adaptive Semantic Specialization (MASS), a semanticaware MoE framework for adaptive expert expansion and dynamic routing. MASS introduces two key advancements: (i) a gradient-based semantic drift detector that prompts targeted expert expansion when the existing expert pool lacks capacity to capture the full semantic diversity of the data, and (ii) an integration of adaptive routing strategy that dynamically adjusts expert usage based on token-level routing confidence mass. We first demonstrate that MASS reliably converges to the point of optimal balance between cost-performance trade-off with notably improved sematic specialization in a highly controlled synthetic setup. Further empirical results on real-world datasets across language and vision domains show that MASS consistently outperforms a range of strong MoE baselines, demonstrating its domain robustness and enhanced expert specialization.

Can TabPFN Compete with GNNs for Node Classification via Graph Tabularization?

Foundation models pretrained on large data have demonstrated remarkable zero-shot generalization capabilities across domains. Building on the success of TabPFN for tabular data and its recent extension to time series, we investigate whether graph node classification can be effectively reformulated as a tabular learning problem. We introduce TabPFN-GN, which transforms graph data into tabular features by extracting node attributes, structural properties, positional encodings, and optionally smoothed neighborhood features. This enables TabPFN to perform direct node classification without any graph-specific training or language model dependencies. Our experiments on 12 benchmark datasets reveal that TabPFN-GN achieves competitive performance with GNNs on homophilous graphs and consistently outperforms them on heterophilous graphs. These results demonstrate that principled feature engineering can bridge the gap between tabular and graph domains, providing a practical alternative to task-specific GNN training and LLM-dependent graph foundation models.

Are Graph Transformers Necessary? Efficient Long-Range Message Passing with Fractal Nodes in MPNNs

Graph Neural Networks (GNNs) have emerged as powerful tools for learning on graph-structured data, but often struggle to balance local and global information. While graph Transformers aim to address this by enabling long-range interactions, they often overlook the inherent locality and efficiency of Message Passing Neural Networks (MPNNs). We propose a new concept called fractal nodes, inspired by the fractal structure observed in real-world networks. Our approach is based on the intuition that graph partitioning naturally induces fractal structure, where subgraphs often reflect the connectivity patterns of the full graph. Fractal nodes are designed to coexist with the original nodes and adaptively aggregate subgraph-level feature representations, thereby enforcing feature similarity within each subgraph. We show that fractal nodes alleviate the over-squashing problem by providing direct shortcut connections that enable long-range propagation of subgraph-level representations. Experiment results show that our method improves the expressive power of MPNNs and achieves comparable or better performance to graph Transformers while maintaining the computational efficiency of MPNN by improving the long-range dependencies of MPNN.

PDEfuncta: Spectrally-Aware Neural Representation for PDE Solution Modeling

Scientific machine learning often involves representing complex solution fields that exhibit high-frequency features such as sharp transitions, fine-scale oscillations, and localized structures. While implicit neural representations (INRs) have shown promise for continuous function modeling, capturing such high-frequency behavior remains a challenge-especially when modeling multiple solution fields with a shared network. Prior work addressing spectral bias in INRs has primarily focused on single-instance settings, limiting scalability and generalization. In this work, we propose Global Fourier Modulation (GFM), a novel modulation technique that injects high-frequency information at each layer of the INR through Fourier-based reparameterization. This enables compact and accurate representation of multiple solution fields using low-dimensional latent vectors. Building upon GFM, we introduce PDEfuncta, a meta-learning framework designed to learn multi-modal solution fields and support generalization to new tasks. Through empirical studies on diverse scientific problems, we demonstrate that our method not only improves representational quality but also shows potential for forward and inverse inference tasks without the need for retraining.

Neural Functions for Learning Periodic Signal

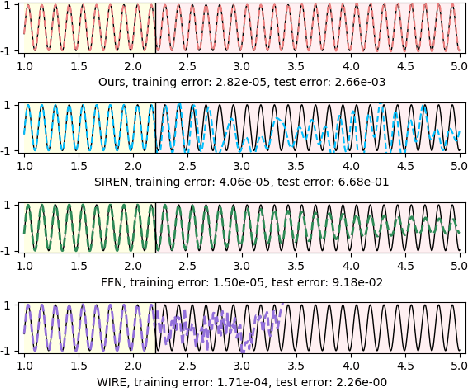
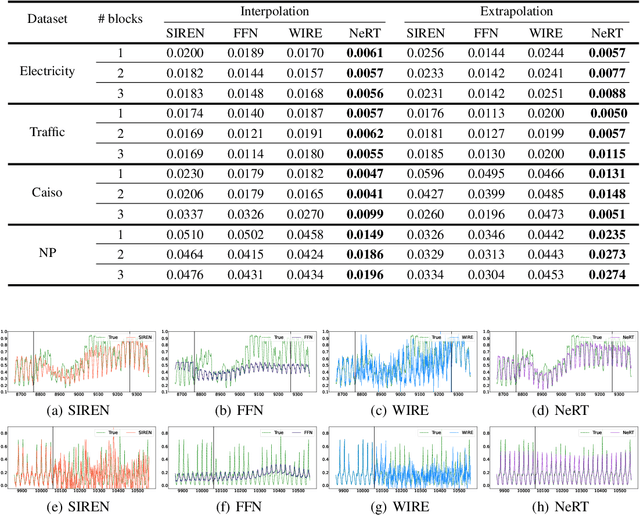
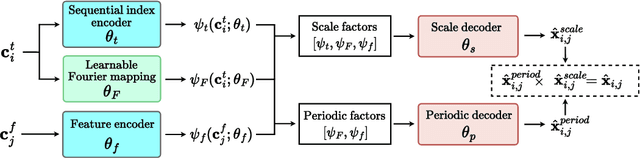
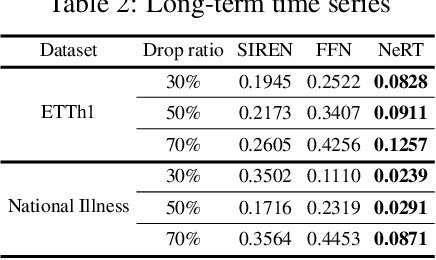
As function approximators, deep neural networks have served as an effective tool to represent various signal types. Recent approaches utilize multi-layer perceptrons (MLPs) to learn a nonlinear mapping from a coordinate to its corresponding signal, facilitating the learning of continuous neural representations from discrete data points. Despite notable successes in learning diverse signal types, coordinate-based MLPs often face issues of overfitting and limited generalizability beyond the training region, resulting in subpar extrapolation performance. This study addresses scenarios where the underlying true signals exhibit periodic properties, either spatially or temporally. We propose a novel network architecture, which extracts periodic patterns from measurements and leverages this information to represent the signal, thereby enhancing generalization and improving extrapolation performance. We demonstrate the efficacy of the proposed method through comprehensive experiments, including the learning of the periodic solutions for differential equations, and time series imputation (interpolation) and forecasting (extrapolation) on real-world datasets.

Learning Advanced Self-Attention for Linear Transformers in the Singular Value Domain

Transformers have demonstrated remarkable performance across diverse domains. The key component of Transformers is self-attention, which learns the relationship between any two tokens in the input sequence. Recent studies have revealed that the self-attention can be understood as a normalized adjacency matrix of a graph. Notably, from the perspective of graph signal processing (GSP), the self-attention can be equivalently defined as a simple graph filter, applying GSP using the value vector as the signal. However, the self-attention is a graph filter defined with only the first order of the polynomial matrix, and acts as a low-pass filter preventing the effective leverage of various frequency information. Consequently, existing self-attention mechanisms are designed in a rather simplified manner. Therefore, we propose a novel method, called \underline{\textbf{A}}ttentive \underline{\textbf{G}}raph \underline{\textbf{F}}ilter (AGF), interpreting the self-attention as learning the graph filter in the singular value domain from the perspective of graph signal processing for directed graphs with the linear complexity w.r.t. the input length $n$, i.e., $\mathcal{O}(nd^2)$. In our experiments, we demonstrate that AGF achieves state-of-the-art performance on various tasks, including Long Range Arena benchmark and time series classification.

Possibility for Proactive Anomaly Detection

Time-series anomaly detection, which detects errors and failures in a workflow, is one of the most important topics in real-world applications. The purpose of time-series anomaly detection is to reduce potential damages or losses. However, existing anomaly detection models detect anomalies through the error between the model output and the ground truth (observed) value, which makes them impractical. In this work, we present a \textit{proactive} approach for time-series anomaly detection based on a time-series forecasting model specialized for anomaly detection and a data-driven anomaly detection model. Our proactive approach establishes an anomaly threshold from training data with a data-driven anomaly detection model, and anomalies are subsequently detected by identifying predicted values that exceed the anomaly threshold. In addition, we extensively evaluated the model using four anomaly detection benchmarks and analyzed both predictable and unpredictable anomalies. We attached the source code as supplementary material.

PIORF: Physics-Informed Ollivier-Ricci Flow for Long-Range Interactions in Mesh Graph Neural Networks

Recently, data-driven simulators based on graph neural networks have gained attention in modeling physical systems on unstructured meshes. However, they struggle with long-range dependencies in fluid flows, particularly in refined mesh regions. This challenge, known as the 'over-squashing' problem, hinders information propagation. While existing graph rewiring methods address this issue to some extent, they only consider graph topology, overlooking the underlying physical phenomena. We propose Physics-Informed Ollivier-Ricci Flow (PIORF), a novel rewiring method that combines physical correlations with graph topology. PIORF uses Ollivier-Ricci curvature (ORC) to identify bottleneck regions and connects these areas with nodes in high-velocity gradient nodes, enabling long-range interactions and mitigating over-squashing. Our approach is computationally efficient in rewiring edges and can scale to larger simulations. Experimental results on 3 fluid dynamics benchmark datasets show that PIORF consistently outperforms baseline models and existing rewiring methods, achieving up to 26.2 improvement.

Unveiling the Potential of Superexpressive Networks in Implicit Neural Representations

In this study, we examine the potential of one of the ``superexpressive'' networks in the context of learning neural functions for representing complex signals and performing machine learning downstream tasks. Our focus is on evaluating their performance on computer vision and scientific machine learning tasks including signal representation/inverse problems and solutions of partial differential equations. Through an empirical investigation in various benchmark tasks, we demonstrate that superexpressive networks, as proposed by [Zhang et al. NeurIPS, 2022], which employ a specialized network structure characterized by having an additional dimension, namely width, depth, and ``height'', can surpass recent implicit neural representations that use highly-specialized nonlinear activation functions.