Neural Functions for Learning Periodic Signal

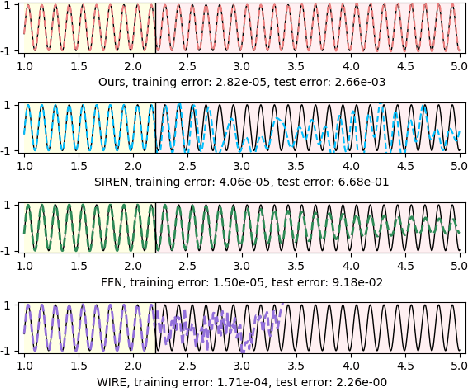
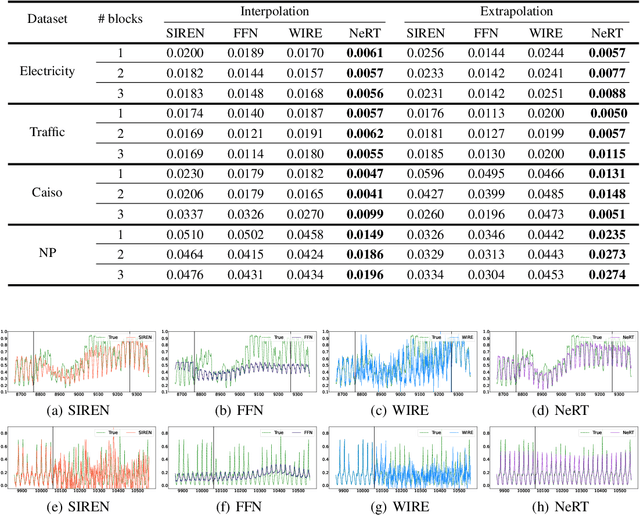
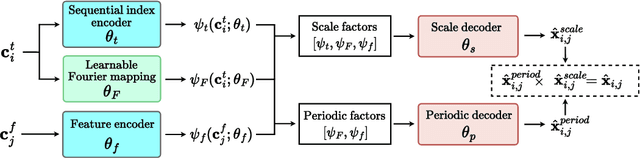
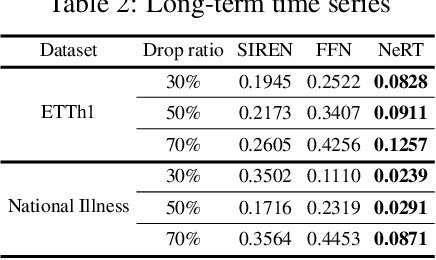
As function approximators, deep neural networks have served as an effective tool to represent various signal types. Recent approaches utilize multi-layer perceptrons (MLPs) to learn a nonlinear mapping from a coordinate to its corresponding signal, facilitating the learning of continuous neural representations from discrete data points. Despite notable successes in learning diverse signal types, coordinate-based MLPs often face issues of overfitting and limited generalizability beyond the training region, resulting in subpar extrapolation performance. This study addresses scenarios where the underlying true signals exhibit periodic properties, either spatially or temporally. We propose a novel network architecture, which extracts periodic patterns from measurements and leverages this information to represent the signal, thereby enhancing generalization and improving extrapolation performance. We demonstrate the efficacy of the proposed method through comprehensive experiments, including the learning of the periodic solutions for differential equations, and time series imputation (interpolation) and forecasting (extrapolation) on real-world datasets.

Unveiling the Potential of Superexpressive Networks in Implicit Neural Representations

In this study, we examine the potential of one of the ``superexpressive'' networks in the context of learning neural functions for representing complex signals and performing machine learning downstream tasks. Our focus is on evaluating their performance on computer vision and scientific machine learning tasks including signal representation/inverse problems and solutions of partial differential equations. Through an empirical investigation in various benchmark tasks, we demonstrate that superexpressive networks, as proposed by [Zhang et al. NeurIPS, 2022], which employ a specialized network structure characterized by having an additional dimension, namely width, depth, and ``height'', can surpass recent implicit neural representations that use highly-specialized nonlinear activation functions.

Tackling Few-Shot Segmentation in Remote Sensing via Inpainting Diffusion Model

Limited data is a common problem in remote sensing due to the high cost of obtaining annotated samples. In the few-shot segmentation task, models are typically trained on base classes with abundant annotations and later adapted to novel classes with limited examples. However, this often necessitates specialized model architectures or complex training strategies. Instead, we propose a simple approach that leverages diffusion models to generate diverse variations of novel-class objects within a given scene, conditioned by the limited examples of the novel classes. By framing the problem as an image inpainting task, we synthesize plausible instances of novel classes under various environments, effectively increasing the number of samples for the novel classes and mitigating overfitting. The generated samples are then assessed using a cosine similarity metric to ensure semantic consistency with the novel classes. Additionally, we employ Segment Anything Model (SAM) to segment the generated samples and obtain precise annotations. By using high-quality synthetic data, we can directly fine-tune off-the-shelf segmentation models. Experimental results demonstrate that our method significantly enhances segmentation performance in low-data regimes, highlighting its potential for real-world remote sensing applications.

MaD-Scientist: AI-based Scientist solving Convection-Diffusion-Reaction Equations Using Massive PINN-Based Prior Data

Large language models (LLMs), like ChatGPT, have shown that even trained with noisy prior data, they can generalize effectively to new tasks through in-context learning (ICL) and pre-training techniques. Motivated by this, we explore whether a similar approach can be applied to scientific foundation models (SFMs). Our methodology is structured as follows: (i) we collect low-cost physics-informed neural network (PINN)-based approximated prior data in the form of solutions to partial differential equations (PDEs) constructed through an arbitrary linear combination of mathematical dictionaries; (ii) we utilize Transformer architectures with self and cross-attention mechanisms to predict PDE solutions without knowledge of the governing equations in a zero-shot setting; (iii) we provide experimental evidence on the one-dimensional convection-diffusion-reaction equation, which demonstrate that pre-training remains robust even with approximated prior data, with only marginal impacts on test accuracy. Notably, this finding opens the path to pre-training SFMs with realistic, low-cost data instead of (or in conjunction with) numerical high-cost data. These results support the conjecture that SFMs can improve in a manner similar to LLMs, where fully cleaning the vast set of sentences crawled from the Internet is nearly impossible.

FastLRNR and Sparse Physics Informed Backpropagation

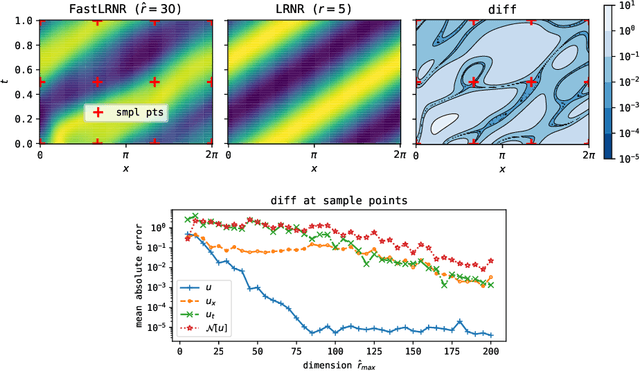
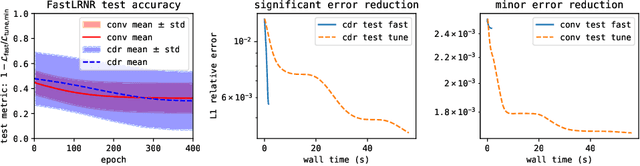
We introduce Sparse Physics Informed Backpropagation (SPInProp), a new class of methods for accelerating backpropagation for a specialized neural network architecture called Low Rank Neural Representation (LRNR). The approach exploits the low rank structure within LRNR and constructs a reduced neural network approximation that is much smaller in size. We call the smaller network FastLRNR. We show that backpropagation of FastLRNR can be substituted for that of LRNR, enabling a significant reduction in complexity. We apply SPInProp to a physics informed neural networks framework and demonstrate how the solution of parametrized partial differential equations is accelerated.

Dense Hand-Object(HO) GraspNet with Full Grasping Taxonomy and Dynamics

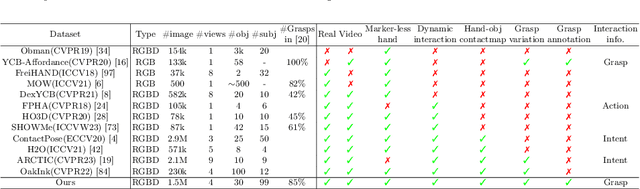
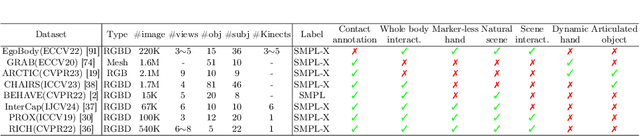
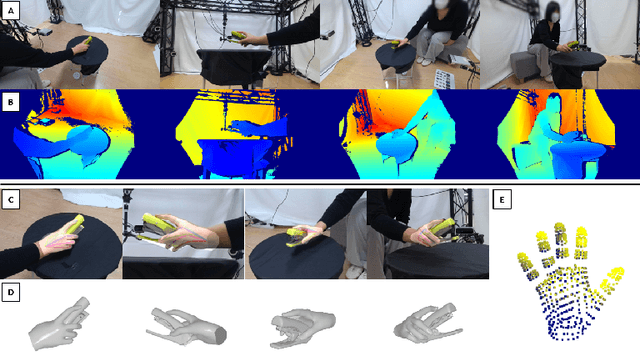
Existing datasets for 3D hand-object interaction are limited either in the data cardinality, data variations in interaction scenarios, or the quality of annotations. In this work, we present a comprehensive new training dataset for hand-object interaction called HOGraspNet. It is the only real dataset that captures full grasp taxonomies, providing grasp annotation and wide intraclass variations. Using grasp taxonomies as atomic actions, their space and time combinatorial can represent complex hand activities around objects. We select 22 rigid objects from the YCB dataset and 8 other compound objects using shape and size taxonomies, ensuring coverage of all hand grasp configurations. The dataset includes diverse hand shapes from 99 participants aged 10 to 74, continuous video frames, and a 1.5M RGB-Depth of sparse frames with annotations. It offers labels for 3D hand and object meshes, 3D keypoints, contact maps, and \emph{grasp labels}. Accurate hand and object 3D meshes are obtained by fitting the hand parametric model (MANO) and the hand implicit function (HALO) to multi-view RGBD frames, with the MoCap system only for objects. Note that HALO fitting does not require any parameter tuning, enabling scalability to the dataset's size with comparable accuracy to MANO. We evaluate HOGraspNet on relevant tasks: grasp classification and 3D hand pose estimation. The result shows performance variations based on grasp type and object class, indicating the potential importance of the interaction space captured by our dataset. The provided data aims at learning universal shape priors or foundation models for 3D hand-object interaction. Our dataset and code are available at https://hograspnet2024.github.io/.

Parameterized Physics-informed Neural Networks for Parameterized PDEs

Complex physical systems are often described by partial differential equations (PDEs) that depend on parameters such as the Reynolds number in fluid mechanics. In applications such as design optimization or uncertainty quantification, solutions of those PDEs need to be evaluated at numerous points in the parameter space. While physics-informed neural networks (PINNs) have emerged as a new strong competitor as a surrogate, their usage in this scenario remains underexplored due to the inherent need for repetitive and time-consuming training. In this paper, we address this problem by proposing a novel extension, parameterized physics-informed neural networks (P$^2$INNs). P$^2$INNs enable modeling the solutions of parameterized PDEs via explicitly encoding a latent representation of PDE parameters. With the extensive empirical evaluation, we demonstrate that P$^2$INNs outperform the baselines both in accuracy and parameter efficiency on benchmark 1D and 2D parameterized PDEs and are also effective in overcoming the known "failure modes".

Learning Flexible Body Collision Dynamics with Hierarchical Contact Mesh Transformer

Recently, many mesh-based graph neural network (GNN) models have been proposed for modeling complex high-dimensional physical systems. Remarkable achievements have been made in significantly reducing the solving time compared to traditional numerical solvers. These methods are typically designed to i) reduce the computational cost in solving physical dynamics and/or ii) propose techniques to enhance the solution accuracy in fluid and rigid body dynamics. However, it remains under-explored whether they are effective in addressing the challenges of flexible body dynamics, where instantaneous collisions occur within a very short timeframe. In this paper, we present Hierarchical Contact Mesh Transformer (HCMT), which uses hierarchical mesh structures and can learn long-range dependencies (occurred by collisions) among spatially distant positions of a body -- two close positions in a higher-level mesh corresponds to two distant positions in a lower-level mesh. HCMT enables long-range interactions, and the hierarchical mesh structure quickly propagates collision effects to faraway positions. To this end, it consists of a contact mesh Transformer and a hierarchical mesh Transformer (CMT and HMT, respectively). Lastly, we propose a flexible body dynamics dataset, consisting of trajectories that reflect experimental settings frequently used in the display industry for product designs. We also compare the performance of several baselines using well-known benchmark datasets. Our results show that HCMT provides significant performance improvements over existing methods.

Operator-learning-inspired Modeling of Neural Ordinary Differential Equations

Neural ordinary differential equations (NODEs), one of the most influential works of the differential equation-based deep learning, are to continuously generalize residual networks and opened a new field. They are currently utilized for various downstream tasks, e.g., image classification, time series classification, image generation, etc. Its key part is how to model the time-derivative of the hidden state, denoted dh(t)/dt. People have habitually used conventional neural network architectures, e.g., fully-connected layers followed by non-linear activations. In this paper, however, we present a neural operator-based method to define the time-derivative term. Neural operators were initially proposed to model the differential operator of partial differential equations (PDEs). Since the time-derivative of NODEs can be understood as a special type of the differential operator, our proposed method, called branched Fourier neural operator (BFNO), makes sense. In our experiments with general downstream tasks, our method significantly outperforms existing methods.

Hypernetwork-based Meta-Learning for Low-Rank Physics-Informed Neural Networks

In various engineering and applied science applications, repetitive numerical simulations of partial differential equations (PDEs) for varying input parameters are often required (e.g., aircraft shape optimization over many design parameters) and solvers are required to perform rapid execution. In this study, we suggest a path that potentially opens up a possibility for physics-informed neural networks (PINNs), emerging deep-learning-based solvers, to be considered as one such solver. Although PINNs have pioneered a proper integration of deep-learning and scientific computing, they require repetitive time-consuming training of neural networks, which is not suitable for many-query scenarios. To address this issue, we propose a lightweight low-rank PINNs containing only hundreds of model parameters and an associated hypernetwork-based meta-learning algorithm, which allows efficient approximation of solutions of PDEs for varying ranges of PDE input parameters. Moreover, we show that the proposed method is effective in overcoming a challenging issue, known as "failure modes" of PINNs.