PDEfuncta: Spectrally-Aware Neural Representation for PDE Solution Modeling

Scientific machine learning often involves representing complex solution fields that exhibit high-frequency features such as sharp transitions, fine-scale oscillations, and localized structures. While implicit neural representations (INRs) have shown promise for continuous function modeling, capturing such high-frequency behavior remains a challenge-especially when modeling multiple solution fields with a shared network. Prior work addressing spectral bias in INRs has primarily focused on single-instance settings, limiting scalability and generalization. In this work, we propose Global Fourier Modulation (GFM), a novel modulation technique that injects high-frequency information at each layer of the INR through Fourier-based reparameterization. This enables compact and accurate representation of multiple solution fields using low-dimensional latent vectors. Building upon GFM, we introduce PDEfuncta, a meta-learning framework designed to learn multi-modal solution fields and support generalization to new tasks. Through empirical studies on diverse scientific problems, we demonstrate that our method not only improves representational quality but also shows potential for forward and inverse inference tasks without the need for retraining.

Neural Functions for Learning Periodic Signal

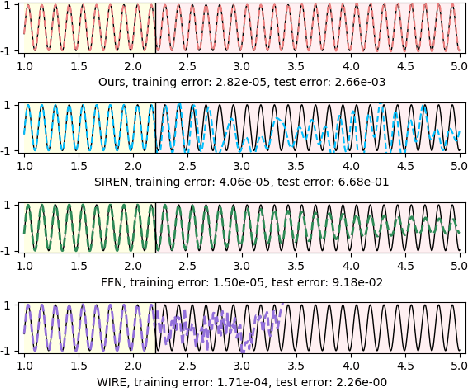
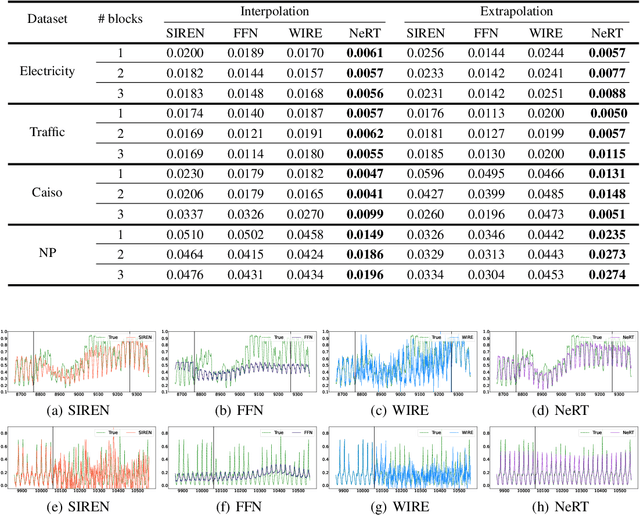
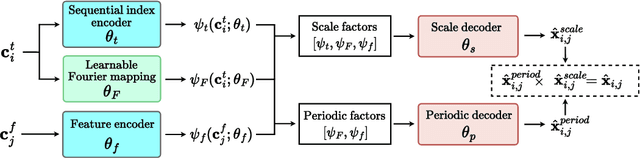
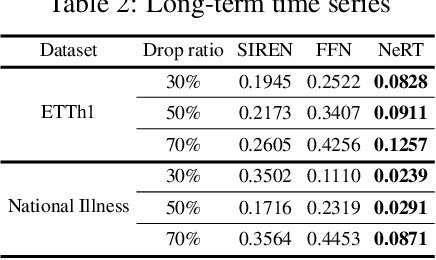
As function approximators, deep neural networks have served as an effective tool to represent various signal types. Recent approaches utilize multi-layer perceptrons (MLPs) to learn a nonlinear mapping from a coordinate to its corresponding signal, facilitating the learning of continuous neural representations from discrete data points. Despite notable successes in learning diverse signal types, coordinate-based MLPs often face issues of overfitting and limited generalizability beyond the training region, resulting in subpar extrapolation performance. This study addresses scenarios where the underlying true signals exhibit periodic properties, either spatially or temporally. We propose a novel network architecture, which extracts periodic patterns from measurements and leverages this information to represent the signal, thereby enhancing generalization and improving extrapolation performance. We demonstrate the efficacy of the proposed method through comprehensive experiments, including the learning of the periodic solutions for differential equations, and time series imputation (interpolation) and forecasting (extrapolation) on real-world datasets.

Unveiling the Potential of Superexpressive Networks in Implicit Neural Representations

In this study, we examine the potential of one of the ``superexpressive'' networks in the context of learning neural functions for representing complex signals and performing machine learning downstream tasks. Our focus is on evaluating their performance on computer vision and scientific machine learning tasks including signal representation/inverse problems and solutions of partial differential equations. Through an empirical investigation in various benchmark tasks, we demonstrate that superexpressive networks, as proposed by [Zhang et al. NeurIPS, 2022], which employ a specialized network structure characterized by having an additional dimension, namely width, depth, and ``height'', can surpass recent implicit neural representations that use highly-specialized nonlinear activation functions.

Parameterized Physics-informed Neural Networks for Parameterized PDEs

Complex physical systems are often described by partial differential equations (PDEs) that depend on parameters such as the Reynolds number in fluid mechanics. In applications such as design optimization or uncertainty quantification, solutions of those PDEs need to be evaluated at numerous points in the parameter space. While physics-informed neural networks (PINNs) have emerged as a new strong competitor as a surrogate, their usage in this scenario remains underexplored due to the inherent need for repetitive and time-consuming training. In this paper, we address this problem by proposing a novel extension, parameterized physics-informed neural networks (P$^2$INNs). P$^2$INNs enable modeling the solutions of parameterized PDEs via explicitly encoding a latent representation of PDE parameters. With the extensive empirical evaluation, we demonstrate that P$^2$INNs outperform the baselines both in accuracy and parameter efficiency on benchmark 1D and 2D parameterized PDEs and are also effective in overcoming the known "failure modes".

Hawkes Process Based on Controlled Differential Equations

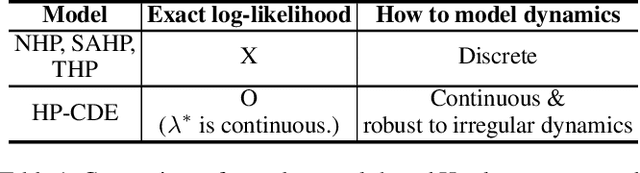
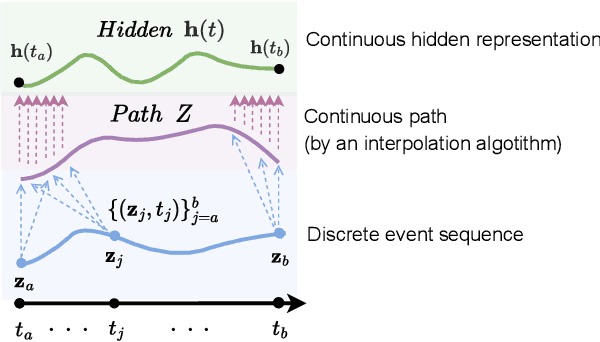
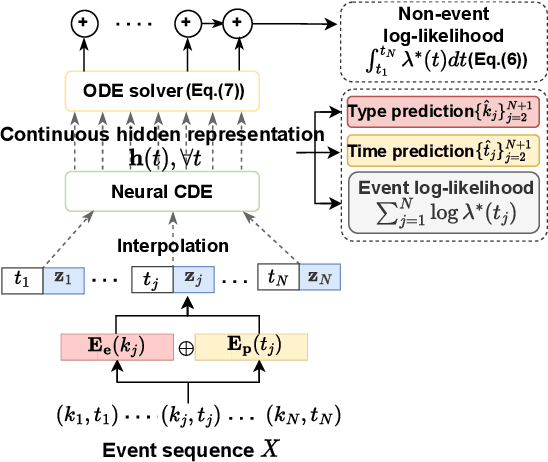
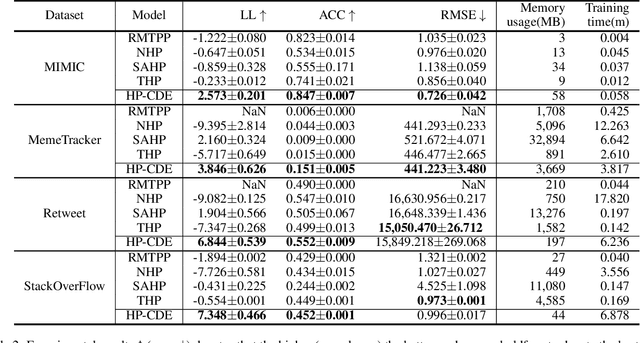
Hawkes processes are a popular framework to model the occurrence of sequential events, i.e., occurrence dynamics, in several fields such as social diffusion. In real-world scenarios, the inter-arrival time among events is irregular. However, existing neural network-based Hawkes process models not only i) fail to capture such complicated irregular dynamics, but also ii) resort to heuristics to calculate the log-likelihood of events since they are mostly based on neural networks designed for regular discrete inputs. To this end, we present the concept of Hawkes process based on controlled differential equations (HP-CDE), by adopting the neural controlled differential equation (neural CDE) technology which is an analogue to continuous RNNs. Since HP-CDE continuously reads data, i) irregular time-series datasets can be properly treated preserving their uneven temporal spaces, and ii) the log-likelihood can be exactly computed. Moreover, as both Hawkes processes and neural CDEs are first developed to model complicated human behavioral dynamics, neural CDE-based Hawkes processes are successful in modeling such occurrence dynamics. In our experiments with 4 real-world datasets, our method outperforms existing methods by non-trivial margins.

Learnable Path in Neural Controlled Differential Equations

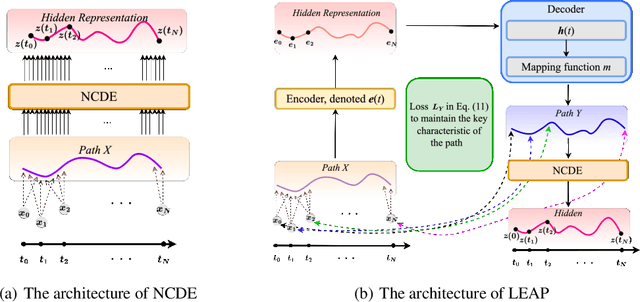
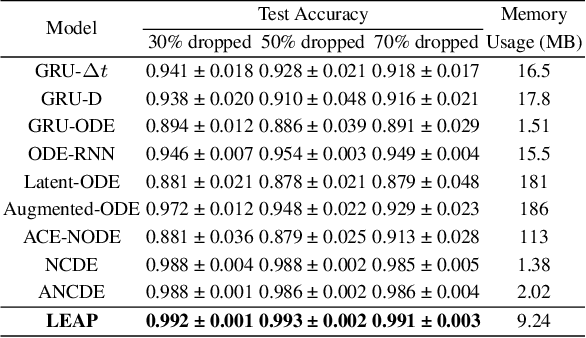
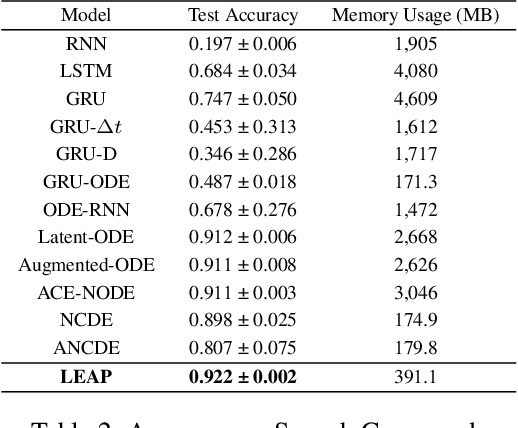
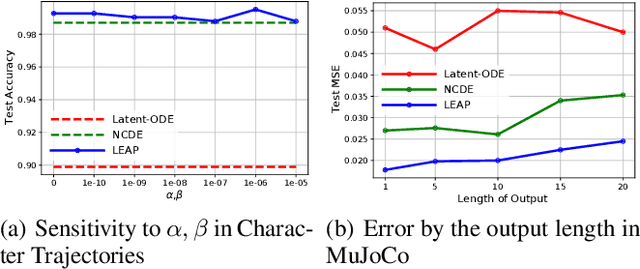
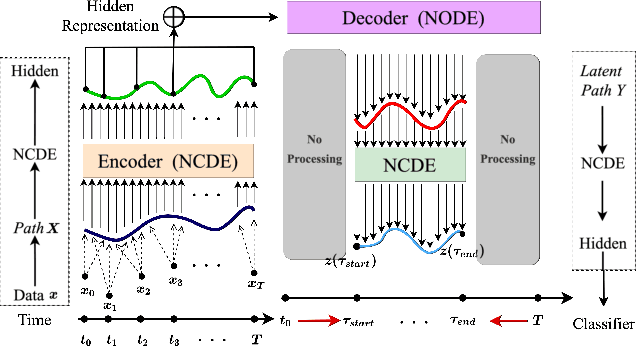
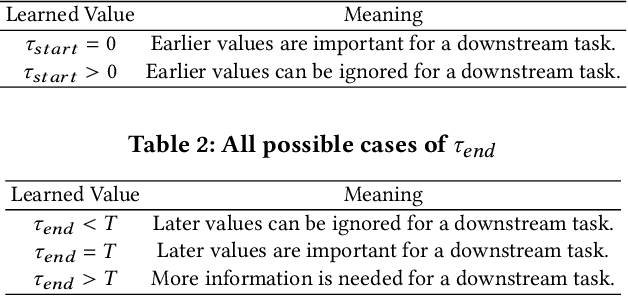
Neural controlled differential equations (NCDEs), which are continuous analogues to recurrent neural networks (RNNs), are a specialized model in (irregular) time-series processing. In comparison with similar models, e.g., neural ordinary differential equations (NODEs), the key distinctive characteristics of NCDEs are i) the adoption of the continuous path created by an interpolation algorithm from each raw discrete time-series sample and ii) the adoption of the Riemann--Stieltjes integral. It is the continuous path which makes NCDEs be analogues to continuous RNNs. However, NCDEs use existing interpolation algorithms to create the path, which is unclear whether they can create an optimal path. To this end, we present a method to generate another latent path (rather than relying on existing interpolation algorithms), which is identical to learning an appropriate interpolation method. We design an encoder-decoder module based on NCDEs and NODEs, and a special training method for it. Our method shows the best performance in both time-series classification and forecasting.

TimeKit: A Time-series Forecasting-based Upgrade Kit for Collaborative Filtering

Recommender systems are a long-standing research problem in data mining and machine learning. They are incremental in nature, as new user-item interaction logs arrive. In real-world applications, we need to periodically train a collaborative filtering algorithm to extract user/item embedding vectors and therefore, a time-series of embedding vectors can be naturally defined. We present a time-series forecasting-based upgrade kit (TimeKit), which works in the following way: it i) first decides a base collaborative filtering algorithm, ii) extracts user/item embedding vectors with the base algorithm from user-item interaction logs incrementally, e.g., every month, iii) trains our time-series forecasting model with the extracted time-series of embedding vectors, and then iv) forecasts the future embedding vectors and recommend with their dot-product scores owing to a recent breakthrough in processing complicated time-series data, i.e., neural controlled differential equations (NCDEs). Our experiments with four real-world benchmark datasets show that the proposed time-series forecasting-based upgrade kit can significantly enhance existing popular collaborative filtering algorithms.

LORD: Lower-Dimensional Embedding of Log-Signature in Neural Rough Differential Equations

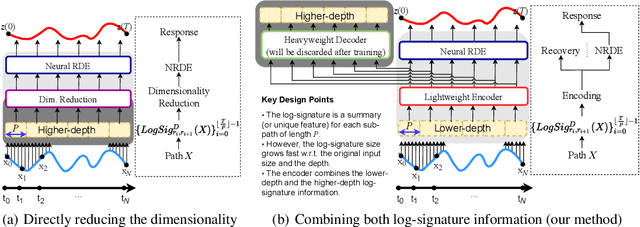
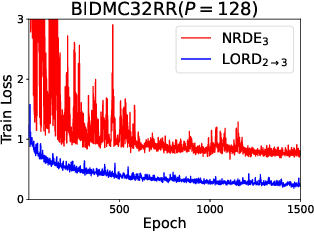
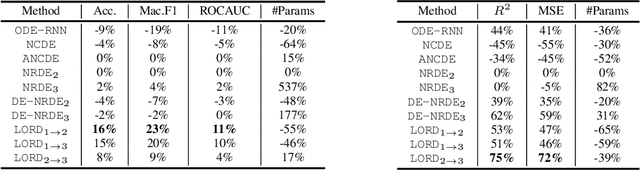
The problem of processing very long time-series data (e.g., a length of more than 10,000) is a long-standing research problem in machine learning. Recently, one breakthrough, called neural rough differential equations (NRDEs), has been proposed and has shown that it is able to process such data. Their main concept is to use the log-signature transform, which is known to be more efficient than the Fourier transform for irregular long time-series, to convert a very long time-series sample into a relatively shorter series of feature vectors. However, the log-signature transform causes non-trivial spatial overheads. To this end, we present the method of LOweR-Dimensional embedding of log-signature (LORD), where we define an NRDE-based autoencoder to implant the higher-depth log-signature knowledge into the lower-depth log-signature. We show that the encoder successfully combines the higher-depth and the lower-depth log-signature knowledge, which greatly stabilizes the training process and increases the model accuracy. In our experiments with benchmark datasets, the improvement ratio by our method is up to 75\% in terms of various classification and forecasting evaluation metrics.

EXIT: Extrapolation and Interpolation-based Neural Controlled Differential Equations for Time-series Classification and Forecasting

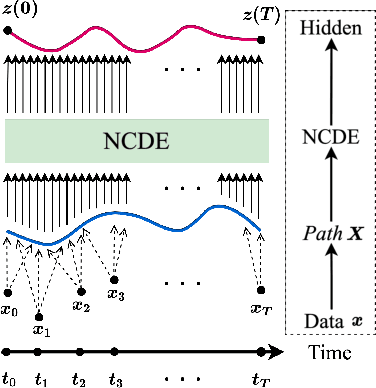
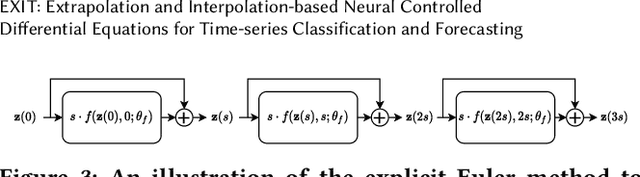
Deep learning inspired by differential equations is a recent research trend and has marked the state of the art performance for many machine learning tasks. Among them, time-series modeling with neural controlled differential equations (NCDEs) is considered as a breakthrough. In many cases, NCDE-based models not only provide better accuracy than recurrent neural networks (RNNs) but also make it possible to process irregular time-series. In this work, we enhance NCDEs by redesigning their core part, i.e., generating a continuous path from a discrete time-series input. NCDEs typically use interpolation algorithms to convert discrete time-series samples to continuous paths. However, we propose to i) generate another latent continuous path using an encoder-decoder architecture, which corresponds to the interpolation process of NCDEs, i.e., our neural network-based interpolation vs. the existing explicit interpolation, and ii) exploit the generative characteristic of the decoder, i.e., extrapolation beyond the time domain of original data if needed. Therefore, our NCDE design can use both the interpolated and the extrapolated information for downstream machine learning tasks. In our experiments with 5 real-world datasets and 12 baselines, our extrapolation and interpolation-based NCDEs outperform existing baselines by non-trivial margins.

LightMove: A Lightweight Next-POI Recommendation for Taxicab Rooftop Advertising

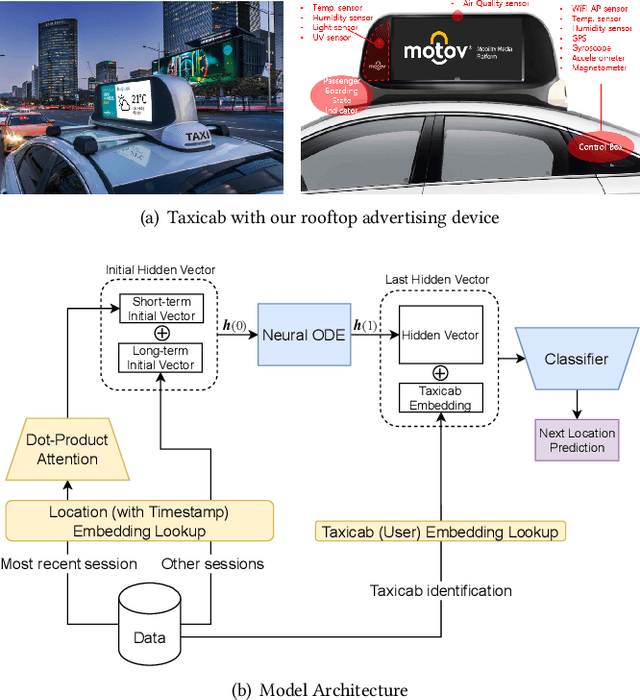
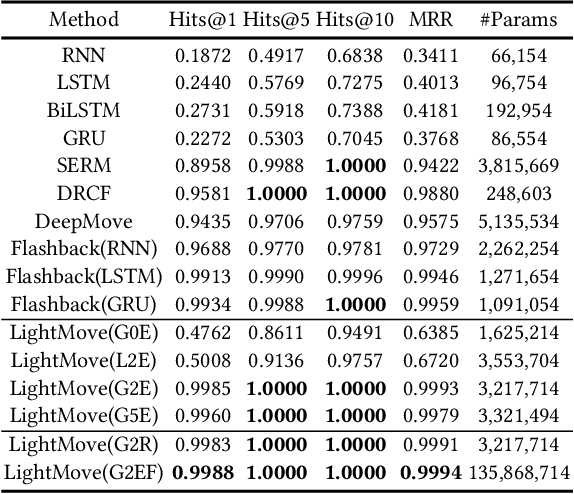
Mobile digital billboards are an effective way to augment brand-awareness. Among various such mobile billboards, taxicab rooftop devices are emerging in the market as a brand new media. Motov is a leading company in South Korea in the taxicab rooftop advertising market. In this work, we present a lightweight yet accurate deep learning-based method to predict taxicabs' next locations to better prepare for targeted advertising based on demographic information of locations. Considering the fact that next POI recommendation datasets are frequently sparse, we design our presented model based on neural ordinary differential equations (NODEs), which are known to be robust to sparse/incorrect input, with several enhancements. Our model, which we call LightMove, has a larger prediction accuracy, a smaller number of parameters, and/or a smaller training/inference time, when evaluating with various datasets, in comparison with state-of-the-art models.