EXIT: Extrapolation and Interpolation-based Neural Controlled Differential Equations for Time-series Classification and Forecasting
Paper and Code
Apr 19, 2022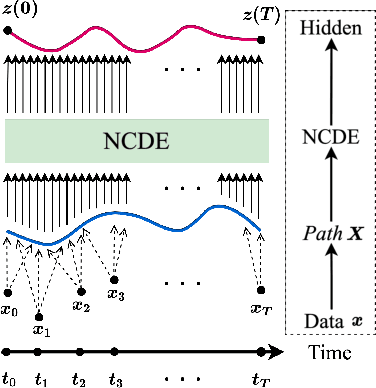
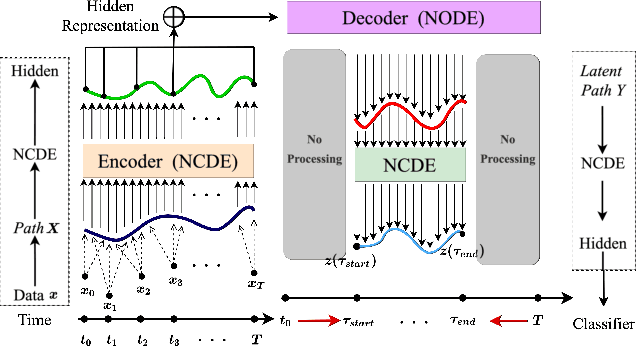
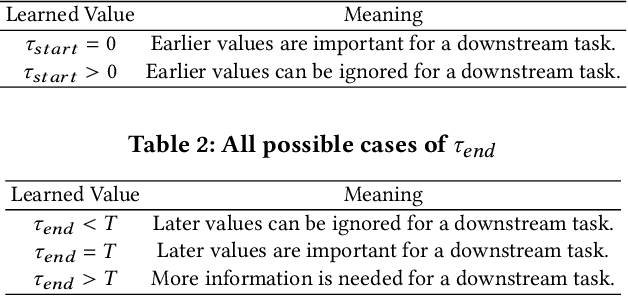
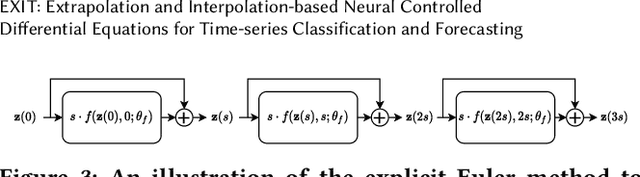
Deep learning inspired by differential equations is a recent research trend and has marked the state of the art performance for many machine learning tasks. Among them, time-series modeling with neural controlled differential equations (NCDEs) is considered as a breakthrough. In many cases, NCDE-based models not only provide better accuracy than recurrent neural networks (RNNs) but also make it possible to process irregular time-series. In this work, we enhance NCDEs by redesigning their core part, i.e., generating a continuous path from a discrete time-series input. NCDEs typically use interpolation algorithms to convert discrete time-series samples to continuous paths. However, we propose to i) generate another latent continuous path using an encoder-decoder architecture, which corresponds to the interpolation process of NCDEs, i.e., our neural network-based interpolation vs. the existing explicit interpolation, and ii) exploit the generative characteristic of the decoder, i.e., extrapolation beyond the time domain of original data if needed. Therefore, our NCDE design can use both the interpolated and the extrapolated information for downstream machine learning tasks. In our experiments with 5 real-world datasets and 12 baselines, our extrapolation and interpolation-based NCDEs outperform existing baselines by non-trivial margins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge