Addressing Prediction Delays in Time Series Forecasting: A Continuous GRU Approach with Derivative Regularization

Time series forecasting has been an essential field in many different application areas, including economic analysis, meteorology, and so forth. The majority of time series forecasting models are trained using the mean squared error (MSE). However, this training based on MSE causes a limitation known as prediction delay. The prediction delay, which implies the ground-truth precedes the prediction, can cause serious problems in a variety of fields, e.g., finance and weather forecasting -- as a matter of fact, predictions succeeding ground-truth observations are not practically meaningful although their MSEs can be low. This paper proposes a new perspective on traditional time series forecasting tasks and introduces a new solution to mitigate the prediction delay. We introduce a continuous-time gated recurrent unit (GRU) based on the neural ordinary differential equation (NODE) which can supervise explicit time-derivatives. We generalize the GRU architecture in a continuous-time manner and minimize the prediction delay through our time-derivative regularization. Our method outperforms in metrics such as MSE, Dynamic Time Warping (DTW) and Time Distortion Index (TDI). In addition, we demonstrate the low prediction delay of our method in a variety of datasets.

Precursor-of-Anomaly Detection for Irregular Time Series

Anomaly detection is an important field that aims to identify unexpected patterns or data points, and it is closely related to many real-world problems, particularly to applications in finance, manufacturing, cyber security, and so on. While anomaly detection has been studied extensively in various fields, detecting future anomalies before they occur remains an unexplored territory. In this paper, we present a novel type of anomaly detection, called \emph{\textbf{P}recursor-of-\textbf{A}nomaly} (PoA) detection. Unlike conventional anomaly detection, which focuses on determining whether a given time series observation is an anomaly or not, PoA detection aims to detect future anomalies before they happen. To solve both problems at the same time, we present a neural controlled differential equation-based neural network and its multi-task learning algorithm. We conduct experiments using 17 baselines and 3 datasets, including regular and irregular time series, and demonstrate that our presented method outperforms the baselines in almost all cases. Our ablation studies also indicate that the multitasking training method significantly enhances the overall performance for both anomaly and PoA detection.

Learnable Path in Neural Controlled Differential Equations

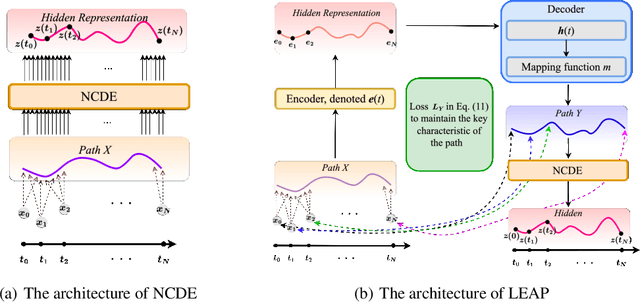
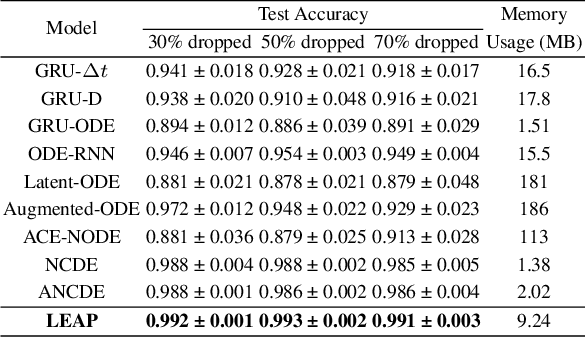
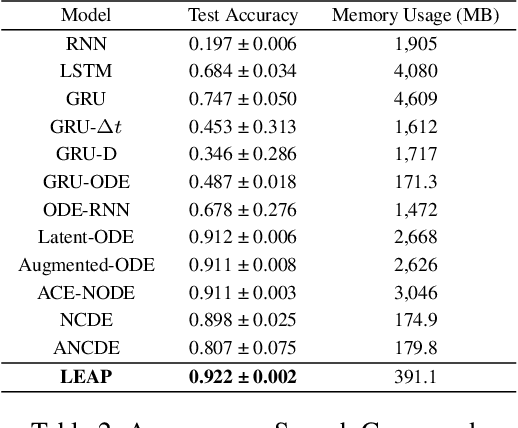
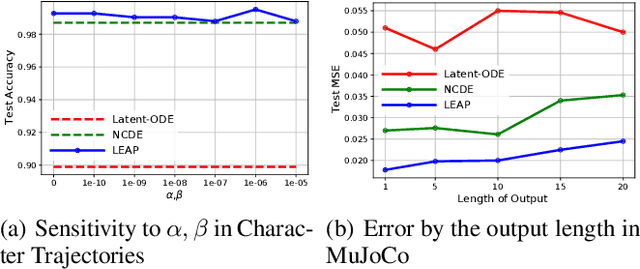
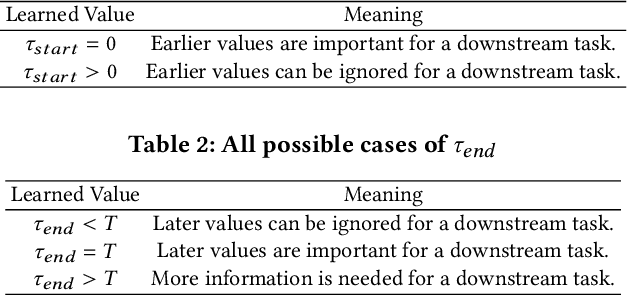
Neural controlled differential equations (NCDEs), which are continuous analogues to recurrent neural networks (RNNs), are a specialized model in (irregular) time-series processing. In comparison with similar models, e.g., neural ordinary differential equations (NODEs), the key distinctive characteristics of NCDEs are i) the adoption of the continuous path created by an interpolation algorithm from each raw discrete time-series sample and ii) the adoption of the Riemann--Stieltjes integral. It is the continuous path which makes NCDEs be analogues to continuous RNNs. However, NCDEs use existing interpolation algorithms to create the path, which is unclear whether they can create an optimal path. To this end, we present a method to generate another latent path (rather than relying on existing interpolation algorithms), which is identical to learning an appropriate interpolation method. We design an encoder-decoder module based on NCDEs and NODEs, and a special training method for it. Our method shows the best performance in both time-series classification and forecasting.

EXIT: Extrapolation and Interpolation-based Neural Controlled Differential Equations for Time-series Classification and Forecasting

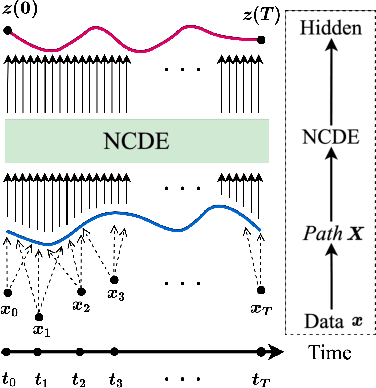
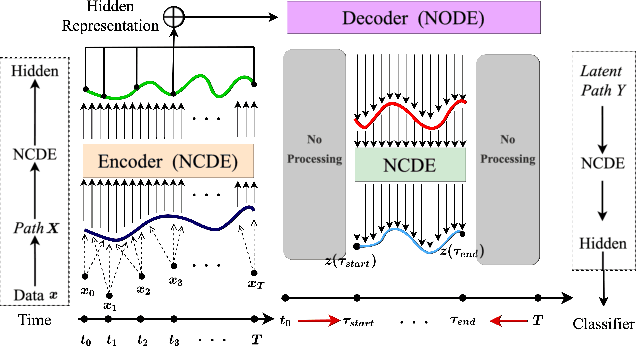
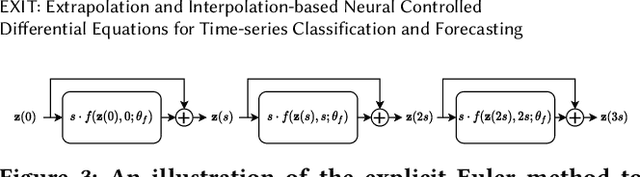
Deep learning inspired by differential equations is a recent research trend and has marked the state of the art performance for many machine learning tasks. Among them, time-series modeling with neural controlled differential equations (NCDEs) is considered as a breakthrough. In many cases, NCDE-based models not only provide better accuracy than recurrent neural networks (RNNs) but also make it possible to process irregular time-series. In this work, we enhance NCDEs by redesigning their core part, i.e., generating a continuous path from a discrete time-series input. NCDEs typically use interpolation algorithms to convert discrete time-series samples to continuous paths. However, we propose to i) generate another latent continuous path using an encoder-decoder architecture, which corresponds to the interpolation process of NCDEs, i.e., our neural network-based interpolation vs. the existing explicit interpolation, and ii) exploit the generative characteristic of the decoder, i.e., extrapolation beyond the time domain of original data if needed. Therefore, our NCDE design can use both the interpolated and the extrapolated information for downstream machine learning tasks. In our experiments with 5 real-world datasets and 12 baselines, our extrapolation and interpolation-based NCDEs outperform existing baselines by non-trivial margins.

Attentive Neural Controlled Differential Equations for Time-series Classification and Forecasting

Neural networks inspired by differential equations have proliferated for the past several years. Neural ordinary differential equations (NODEs) and neural controlled differential equations (NCDEs) are two representative examples of them. In theory, NCDEs provide better representation learning capability for time-series data than NODEs. In particular, it is known that NCDEs are suitable for processing irregular time-series data. Whereas NODEs have been successfully extended after adopting attention, however, it had not been studied yet how to integrate attention into NCDEs. To this end, we present the method of Attentive Neural Controlled Differential Equations (ANCDEs) for time-series classification and forecasting, where dual NCDEs are used: one for generating attention values, and the other for evolving hidden vectors for a downstream machine learning task. We conduct experiments with three real-world time-series datasets and 10 baselines. After dropping some values, we also conduct irregular time-series experiments. Our method consistently shows the best accuracy in all cases by non-trivial margins. Our visualizations also show that the presented attention mechanism works as intended by focusing on crucial information.

ACE-NODE: Attentive Co-Evolving Neural Ordinary Differential Equations

Neural ordinary differential equations (NODEs) presented a new paradigm to construct (continuous-time) neural networks. While showing several good characteristics in terms of the number of parameters and the flexibility in constructing neural networks, they also have a couple of well-known limitations: i) theoretically NODEs learn homeomorphic mapping functions only, and ii) sometimes NODEs show numerical instability in solving integral problems. To handle this, many enhancements have been proposed. To our knowledge, however, integrating attention into NODEs has been overlooked for a while. To this end, we present a novel method of attentive dual co-evolving NODE (ACE-NODE): one main NODE for a downstream machine learning task and the other for providing attention to the main NODE. Our ACE-NODE supports both pairwise and elementwise attention. In our experiments, our method outperforms existing NODE-based and non-NODE-based baselines in almost all cases by non-trivial margins.