Hawkes Process Based on Controlled Differential Equations

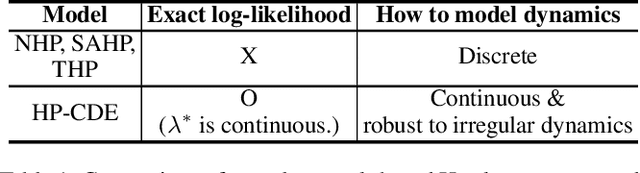
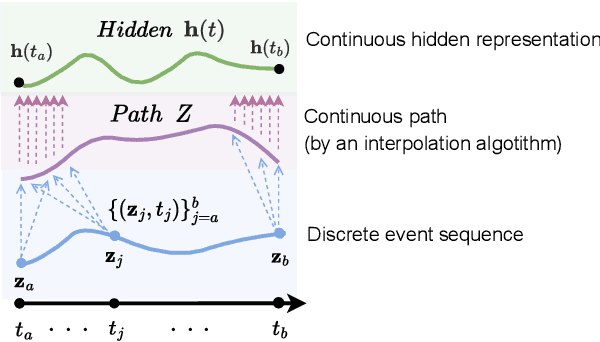
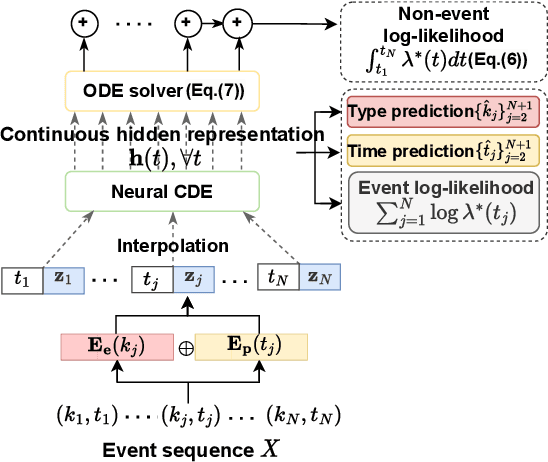
Hawkes processes are a popular framework to model the occurrence of sequential events, i.e., occurrence dynamics, in several fields such as social diffusion. In real-world scenarios, the inter-arrival time among events is irregular. However, existing neural network-based Hawkes process models not only i) fail to capture such complicated irregular dynamics, but also ii) resort to heuristics to calculate the log-likelihood of events since they are mostly based on neural networks designed for regular discrete inputs. To this end, we present the concept of Hawkes process based on controlled differential equations (HP-CDE), by adopting the neural controlled differential equation (neural CDE) technology which is an analogue to continuous RNNs. Since HP-CDE continuously reads data, i) irregular time-series datasets can be properly treated preserving their uneven temporal spaces, and ii) the log-likelihood can be exactly computed. Moreover, as both Hawkes processes and neural CDEs are first developed to model complicated human behavioral dynamics, neural CDE-based Hawkes processes are successful in modeling such occurrence dynamics. In our experiments with 4 real-world datasets, our method outperforms existing methods by non-trivial margins.

Learnable Path in Neural Controlled Differential Equations

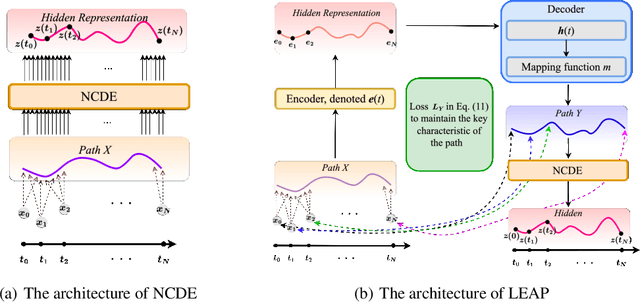
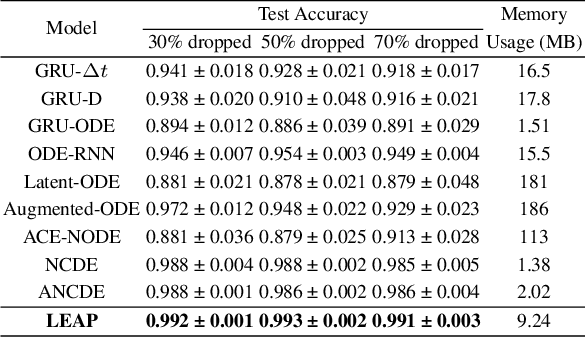
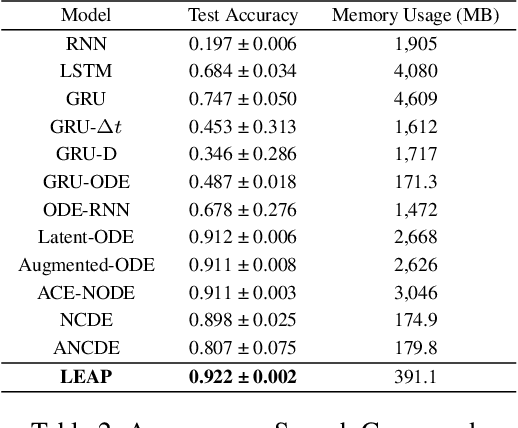
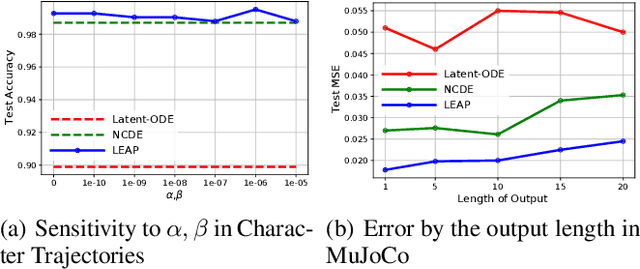
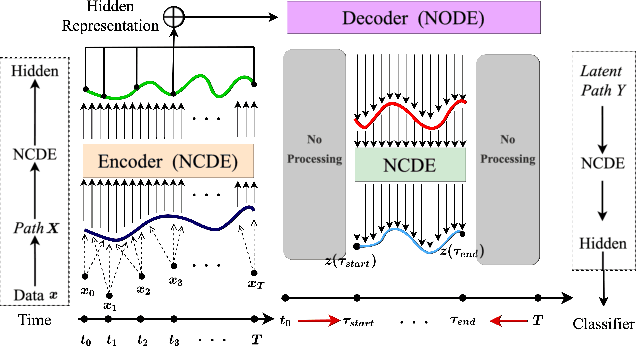
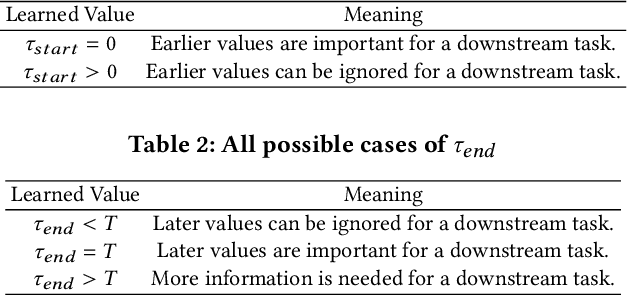
Neural controlled differential equations (NCDEs), which are continuous analogues to recurrent neural networks (RNNs), are a specialized model in (irregular) time-series processing. In comparison with similar models, e.g., neural ordinary differential equations (NODEs), the key distinctive characteristics of NCDEs are i) the adoption of the continuous path created by an interpolation algorithm from each raw discrete time-series sample and ii) the adoption of the Riemann--Stieltjes integral. It is the continuous path which makes NCDEs be analogues to continuous RNNs. However, NCDEs use existing interpolation algorithms to create the path, which is unclear whether they can create an optimal path. To this end, we present a method to generate another latent path (rather than relying on existing interpolation algorithms), which is identical to learning an appropriate interpolation method. We design an encoder-decoder module based on NCDEs and NODEs, and a special training method for it. Our method shows the best performance in both time-series classification and forecasting.

TimeKit: A Time-series Forecasting-based Upgrade Kit for Collaborative Filtering

Recommender systems are a long-standing research problem in data mining and machine learning. They are incremental in nature, as new user-item interaction logs arrive. In real-world applications, we need to periodically train a collaborative filtering algorithm to extract user/item embedding vectors and therefore, a time-series of embedding vectors can be naturally defined. We present a time-series forecasting-based upgrade kit (TimeKit), which works in the following way: it i) first decides a base collaborative filtering algorithm, ii) extracts user/item embedding vectors with the base algorithm from user-item interaction logs incrementally, e.g., every month, iii) trains our time-series forecasting model with the extracted time-series of embedding vectors, and then iv) forecasts the future embedding vectors and recommend with their dot-product scores owing to a recent breakthrough in processing complicated time-series data, i.e., neural controlled differential equations (NCDEs). Our experiments with four real-world benchmark datasets show that the proposed time-series forecasting-based upgrade kit can significantly enhance existing popular collaborative filtering algorithms.

EXIT: Extrapolation and Interpolation-based Neural Controlled Differential Equations for Time-series Classification and Forecasting

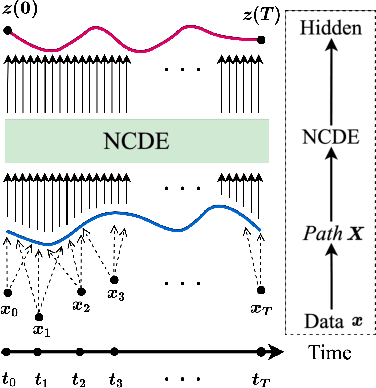
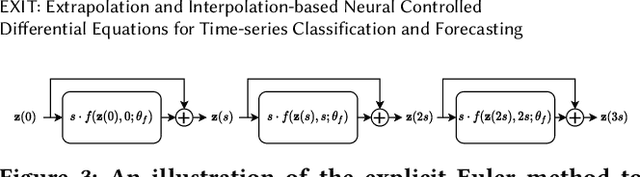
Deep learning inspired by differential equations is a recent research trend and has marked the state of the art performance for many machine learning tasks. Among them, time-series modeling with neural controlled differential equations (NCDEs) is considered as a breakthrough. In many cases, NCDE-based models not only provide better accuracy than recurrent neural networks (RNNs) but also make it possible to process irregular time-series. In this work, we enhance NCDEs by redesigning their core part, i.e., generating a continuous path from a discrete time-series input. NCDEs typically use interpolation algorithms to convert discrete time-series samples to continuous paths. However, we propose to i) generate another latent continuous path using an encoder-decoder architecture, which corresponds to the interpolation process of NCDEs, i.e., our neural network-based interpolation vs. the existing explicit interpolation, and ii) exploit the generative characteristic of the decoder, i.e., extrapolation beyond the time domain of original data if needed. Therefore, our NCDE design can use both the interpolated and the extrapolated information for downstream machine learning tasks. In our experiments with 5 real-world datasets and 12 baselines, our extrapolation and interpolation-based NCDEs outperform existing baselines by non-trivial margins.