PAC-FNO: Parallel-Structured All-Component Fourier Neural Operators for Recognizing Low-Quality Images

A standard practice in developing image recognition models is to train a model on a specific image resolution and then deploy it. However, in real-world inference, models often encounter images different from the training sets in resolution and/or subject to natural variations such as weather changes, noise types and compression artifacts. While traditional solutions involve training multiple models for different resolutions or input variations, these methods are computationally expensive and thus do not scale in practice. To this end, we propose a novel neural network model, parallel-structured and all-component Fourier neural operator (PAC-FNO), that addresses the problem. Unlike conventional feed-forward neural networks, PAC-FNO operates in the frequency domain, allowing it to handle images of varying resolutions within a single model. We also propose a two-stage algorithm for training PAC-FNO with a minimal modification to the original, downstream model. Moreover, the proposed PAC-FNO is ready to work with existing image recognition models. Extensively evaluating methods with seven image recognition benchmarks, we show that the proposed PAC-FNO improves the performance of existing baseline models on images with various resolutions by up to 77.1% and various types of natural variations in the images at inference.

Operator-learning-inspired Modeling of Neural Ordinary Differential Equations

Neural ordinary differential equations (NODEs), one of the most influential works of the differential equation-based deep learning, are to continuously generalize residual networks and opened a new field. They are currently utilized for various downstream tasks, e.g., image classification, time series classification, image generation, etc. Its key part is how to model the time-derivative of the hidden state, denoted dh(t)/dt. People have habitually used conventional neural network architectures, e.g., fully-connected layers followed by non-linear activations. In this paper, however, we present a neural operator-based method to define the time-derivative term. Neural operators were initially proposed to model the differential operator of partial differential equations (PDEs). Since the time-derivative of NODEs can be understood as a special type of the differential operator, our proposed method, called branched Fourier neural operator (BFNO), makes sense. In our experiments with general downstream tasks, our method significantly outperforms existing methods.

Long-term Time Series Forecasting based on Decomposition and Neural Ordinary Differential Equations

Long-term time series forecasting (LTSF) is a challenging task that has been investigated in various domains such as finance investment, health care, traffic, and weather forecasting. In recent years, Linear-based LTSF models showed better performance, pointing out the problem of Transformer-based approaches causing temporal information loss. However, Linear-based approach has also limitations that the model is too simple to comprehensively exploit the characteristics of the dataset. To solve these limitations, we propose LTSF-DNODE, which applies a model based on linear ordinary differential equations (ODEs) and a time series decomposition method according to data statistical characteristics. We show that LTSF-DNODE outperforms the baselines on various real-world datasets. In addition, for each dataset, we explore the impacts of regularization in the neural ordinary differential equation (NODE) framework.

GT-GAN: General Purpose Time Series Synthesis with Generative Adversarial Networks

Time series synthesis is an important research topic in the field of deep learning, which can be used for data augmentation. Time series data types can be broadly classified into regular or irregular. However, there are no existing generative models that show good performance for both types without any model changes. Therefore, we present a general purpose model capable of synthesizing regular and irregular time series data. To our knowledge, we are the first designing a general purpose time series synthesis model, which is one of the most challenging settings for time series synthesis. To this end, we design a generative adversarial network-based method, where many related techniques are carefully integrated into a single framework, ranging from neural ordinary/controlled differential equations to continuous time-flow processes. Our method outperforms all existing methods.

SPI-GAN: Distilling Score-based Generative Models with Straight-Path Interpolations

Score-based generative models (SGMs) are a recently proposed paradigm for deep generative tasks and now show the state-of-the-art sampling performance. It is known that the original SGM design solves the two problems of the generative trilemma: i) sampling quality, and ii) sampling diversity. However, the last problem of the trilemma was not solved, i.e., their training/sampling complexity is notoriously high. To this end, distilling SGMs into simpler models, e.g., generative adversarial networks (GANs), is gathering much attention currently. We present an enhanced distillation method, called straight-path interpolation GAN (SPI-GAN), which can be compared to the state-of-the-art shortcut-based distillation method, called denoising diffusion GAN (DD-GAN). However, our method corresponds to an extreme method that does not use any intermediate shortcut information of the reverse SDE path, in which case DD-GAN fails to obtain good results. Nevertheless, our straight-path interpolation method greatly stabilizes the overall training process. As a result, SPI-GAN is one of the best models in terms of the sampling quality/diversity/time for CIFAR-10, CelebA-HQ-256, and LSUN-Church-256.

LORD: Lower-Dimensional Embedding of Log-Signature in Neural Rough Differential Equations

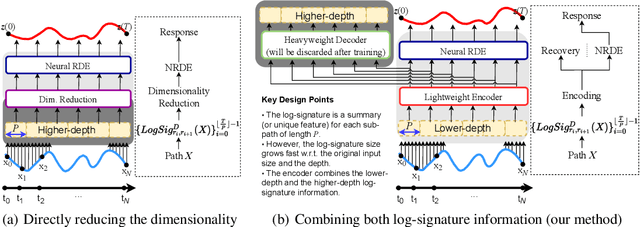
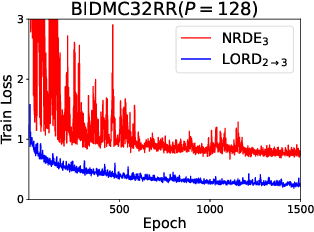
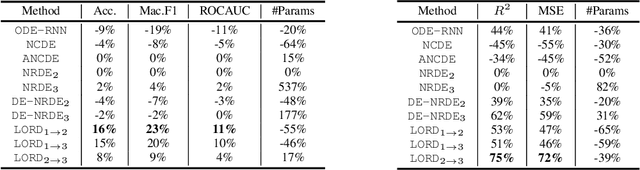
The problem of processing very long time-series data (e.g., a length of more than 10,000) is a long-standing research problem in machine learning. Recently, one breakthrough, called neural rough differential equations (NRDEs), has been proposed and has shown that it is able to process such data. Their main concept is to use the log-signature transform, which is known to be more efficient than the Fourier transform for irregular long time-series, to convert a very long time-series sample into a relatively shorter series of feature vectors. However, the log-signature transform causes non-trivial spatial overheads. To this end, we present the method of LOweR-Dimensional embedding of log-signature (LORD), where we define an NRDE-based autoencoder to implant the higher-depth log-signature knowledge into the lower-depth log-signature. We show that the encoder successfully combines the higher-depth and the lower-depth log-signature knowledge, which greatly stabilizes the training process and increases the model accuracy. In our experiments with benchmark datasets, the improvement ratio by our method is up to 75\% in terms of various classification and forecasting evaluation metrics.

EXIT: Extrapolation and Interpolation-based Neural Controlled Differential Equations for Time-series Classification and Forecasting

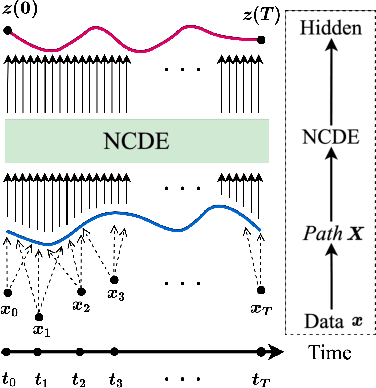
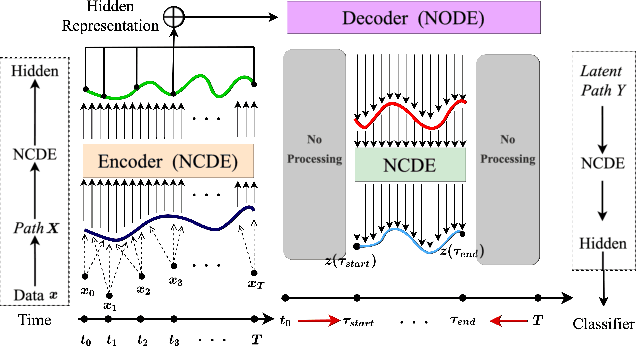
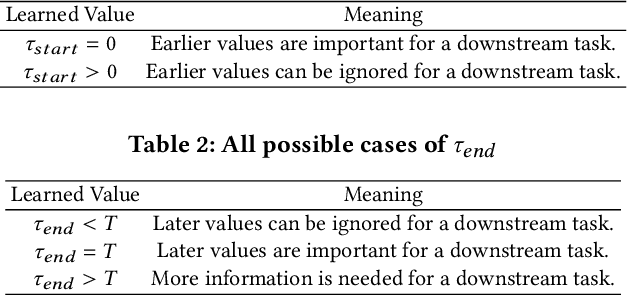
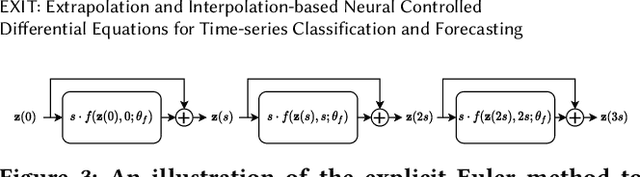
Deep learning inspired by differential equations is a recent research trend and has marked the state of the art performance for many machine learning tasks. Among them, time-series modeling with neural controlled differential equations (NCDEs) is considered as a breakthrough. In many cases, NCDE-based models not only provide better accuracy than recurrent neural networks (RNNs) but also make it possible to process irregular time-series. In this work, we enhance NCDEs by redesigning their core part, i.e., generating a continuous path from a discrete time-series input. NCDEs typically use interpolation algorithms to convert discrete time-series samples to continuous paths. However, we propose to i) generate another latent continuous path using an encoder-decoder architecture, which corresponds to the interpolation process of NCDEs, i.e., our neural network-based interpolation vs. the existing explicit interpolation, and ii) exploit the generative characteristic of the decoder, i.e., extrapolation beyond the time domain of original data if needed. Therefore, our NCDE design can use both the interpolated and the extrapolated information for downstream machine learning tasks. In our experiments with 5 real-world datasets and 12 baselines, our extrapolation and interpolation-based NCDEs outperform existing baselines by non-trivial margins.

Invertible Tabular GANs: Killing Two Birds with OneStone for Tabular Data Synthesis

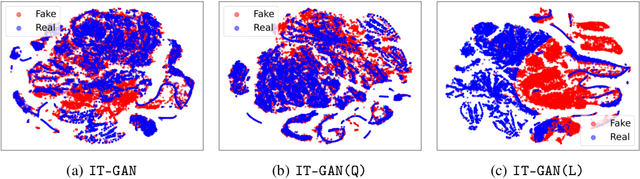
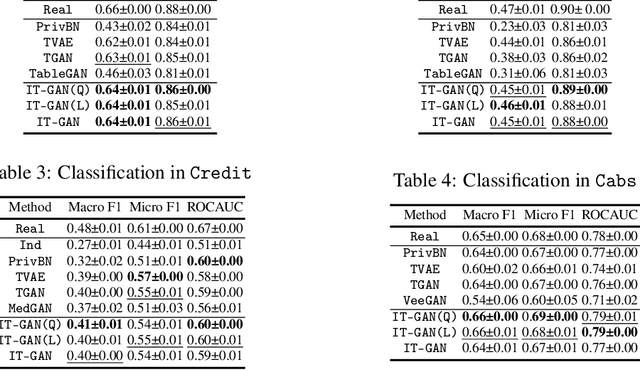
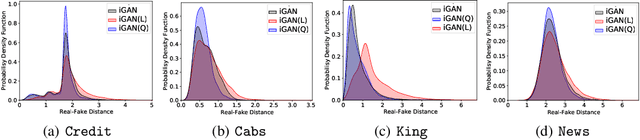
Tabular data synthesis has received wide attention in the literature. This is because available data is often limited, incomplete, or cannot be obtained easily, and data privacy is becoming increasingly important. In this work, we present a generalized GAN framework for tabular synthesis, which combines the adversarial training of GANs and the negative log-density regularization of invertible neural networks. The proposed framework can be used for two distinctive objectives. First, we can further improve the synthesis quality, by decreasing the negative log-density of real records in the process of adversarial training. On the other hand, by increasing the negative log-density of real records, realistic fake records can be synthesized in a way that they are not too much close to real records and reduce the chance of potential information leakage. We conduct experiments with real-world datasets for classification, regression, and privacy attacks. In general, the proposed method demonstrates the best synthesis quality (in terms of task-oriented evaluation metrics, e.g., F1) when decreasing the negative log-density during the adversarial training. If increasing the negative log-density, our experimental results show that the distance between real and fake records increases, enhancing robustness against privacy attacks.

Linear, or Non-Linear, That is the Question!

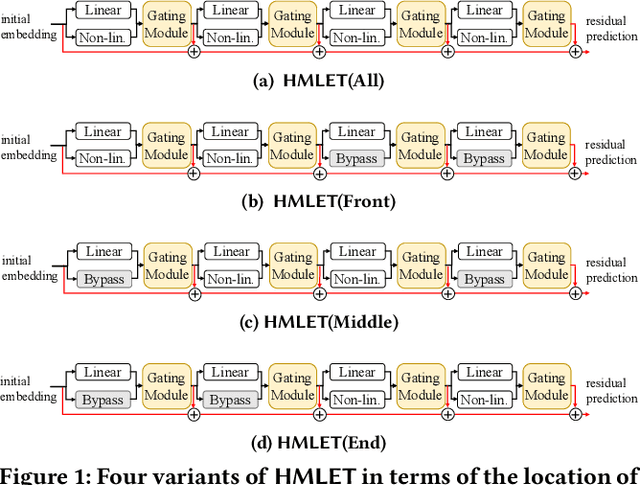
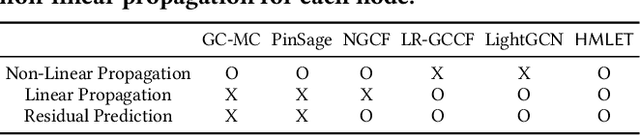
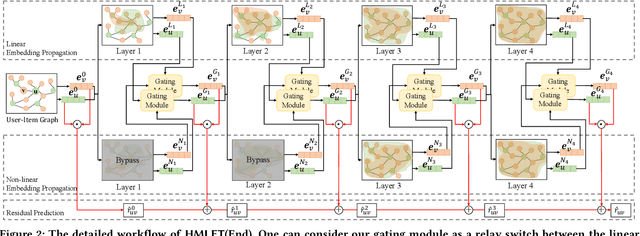
There were fierce debates on whether the non-linear embedding propagation of GCNs is appropriate to GCN-based recommender systems. It was recently found that the linear embedding propagation shows better accuracy than the non-linear embedding propagation. Since this phenomenon was discovered especially in recommender systems, it is required that we carefully analyze the linearity and non-linearity issue. In this work, therefore, we revisit the issues of i) which of the linear or non-linear propagation is better and ii) which factors of users/items decide the linearity/non-linearity of the embedding propagation. We propose a novel Hybrid Method of Linear and non-linEar collaborative filTering method (HMLET, pronounced as Hamlet). In our design, there exist both linear and non-linear propagation steps, when processing each user or item node, and our gating module chooses one of them, which results in a hybrid model of the linear and non-linear GCN-based collaborative filtering (CF). The proposed model yields the best accuracy in three public benchmark datasets. Moreover, we classify users/items into the following three classes depending on our gating modules' selections: Full-Non-Linearity (FNL), Partial-Non-Linearity (PNL), and Full-Linearity (FL). We found that there exist strong correlations between nodes' centrality and their class membership, i.e., important user/item nodes exhibit more preferences towards the non-linearity during the propagation steps. To our knowledge, we are the first who designs a hybrid method and reports the correlation between the graph centrality and the linearity/non-linearity of nodes. All HMLET codes and datasets are available at: https://github.com/qbxlvnf11/HMLET.

LightMove: A Lightweight Next-POI Recommendation for Taxicab Rooftop Advertising

Mobile digital billboards are an effective way to augment brand-awareness. Among various such mobile billboards, taxicab rooftop devices are emerging in the market as a brand new media. Motov is a leading company in South Korea in the taxicab rooftop advertising market. In this work, we present a lightweight yet accurate deep learning-based method to predict taxicabs' next locations to better prepare for targeted advertising based on demographic information of locations. Considering the fact that next POI recommendation datasets are frequently sparse, we design our presented model based on neural ordinary differential equations (NODEs), which are known to be robust to sparse/incorrect input, with several enhancements. Our model, which we call LightMove, has a larger prediction accuracy, a smaller number of parameters, and/or a smaller training/inference time, when evaluating with various datasets, in comparison with state-of-the-art models.