Taeyong Kong
Linear, or Non-Linear, That is the Question!
Nov 14, 2021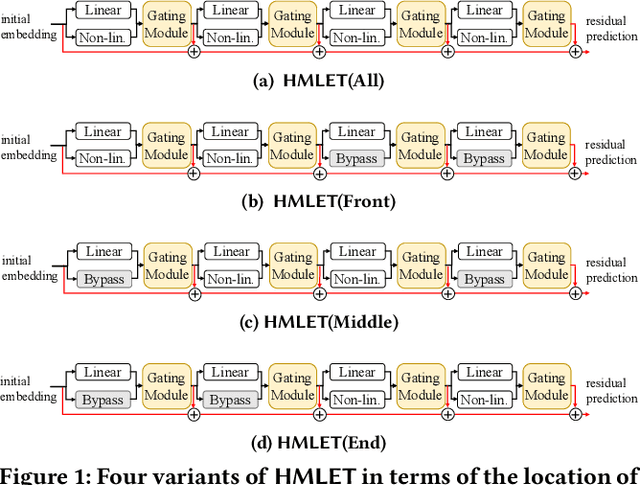

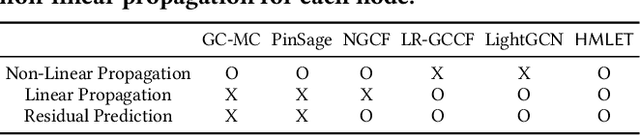
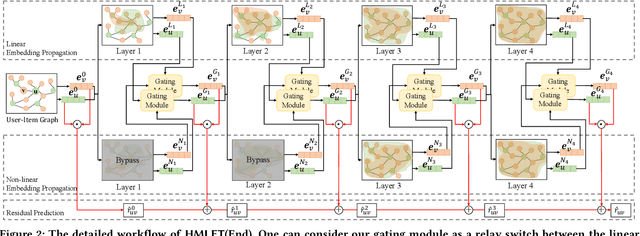
Abstract:There were fierce debates on whether the non-linear embedding propagation of GCNs is appropriate to GCN-based recommender systems. It was recently found that the linear embedding propagation shows better accuracy than the non-linear embedding propagation. Since this phenomenon was discovered especially in recommender systems, it is required that we carefully analyze the linearity and non-linearity issue. In this work, therefore, we revisit the issues of i) which of the linear or non-linear propagation is better and ii) which factors of users/items decide the linearity/non-linearity of the embedding propagation. We propose a novel Hybrid Method of Linear and non-linEar collaborative filTering method (HMLET, pronounced as Hamlet). In our design, there exist both linear and non-linear propagation steps, when processing each user or item node, and our gating module chooses one of them, which results in a hybrid model of the linear and non-linear GCN-based collaborative filtering (CF). The proposed model yields the best accuracy in three public benchmark datasets. Moreover, we classify users/items into the following three classes depending on our gating modules' selections: Full-Non-Linearity (FNL), Partial-Non-Linearity (PNL), and Full-Linearity (FL). We found that there exist strong correlations between nodes' centrality and their class membership, i.e., important user/item nodes exhibit more preferences towards the non-linearity during the propagation steps. To our knowledge, we are the first who designs a hybrid method and reports the correlation between the graph centrality and the linearity/non-linearity of nodes. All HMLET codes and datasets are available at: https://github.com/qbxlvnf11/HMLET.
ACE-NODE: Attentive Co-Evolving Neural Ordinary Differential Equations
May 31, 2021



Abstract:Neural ordinary differential equations (NODEs) presented a new paradigm to construct (continuous-time) neural networks. While showing several good characteristics in terms of the number of parameters and the flexibility in constructing neural networks, they also have a couple of well-known limitations: i) theoretically NODEs learn homeomorphic mapping functions only, and ii) sometimes NODEs show numerical instability in solving integral problems. To handle this, many enhancements have been proposed. To our knowledge, however, integrating attention into NODEs has been overlooked for a while. To this end, we present a novel method of attentive dual co-evolving NODE (ACE-NODE): one main NODE for a downstream machine learning task and the other for providing attention to the main NODE. Our ACE-NODE supports both pairwise and elementwise attention. In our experiments, our method outperforms existing NODE-based and non-NODE-based baselines in almost all cases by non-trivial margins.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge