SVD-AE: Simple Autoencoders for Collaborative Filtering

Collaborative filtering (CF) methods for recommendation systems have been extensively researched, ranging from matrix factorization and autoencoder-based to graph filtering-based methods. Recently, lightweight methods that require almost no training have been recently proposed to reduce overall computation. However, existing methods still have room to improve the trade-offs among accuracy, efficiency, and robustness. In particular, there are no well-designed closed-form studies for \emph{balanced} CF in terms of the aforementioned trade-offs. In this paper, we design SVD-AE, a simple yet effective singular vector decomposition (SVD)-based linear autoencoder, whose closed-form solution can be defined based on SVD for CF. SVD-AE does not require iterative training processes as its closed-form solution can be calculated at once. Furthermore, given the noisy nature of the rating matrix, we explore the robustness against such noisy interactions of existing CF methods and our SVD-AE. As a result, we demonstrate that our simple design choice based on truncated SVD can be used to strengthen the noise robustness of the recommendation while improving efficiency. Code is available at https://github.com/seoyoungh/svd-ae.

GREAD: Graph Neural Reaction-Diffusion Equations

Graph neural networks (GNNs) are one of the most popular research topics for deep learning. GNN methods typically have been designed on top of the graph signal processing theory. In particular, diffusion equations have been widely used for designing the core processing layer of GNNs and therefore, they are inevitably vulnerable to the oversmoothing problem. Recently, a couple of papers paid attention to reaction equations in conjunctions with diffusion equations. However, they all consider limited forms of reaction equations. To this end, we present a reaction-diffusion equation-based GNN method that considers all popular types of reaction equations in addition to one special reaction equation designed by us. To our knowledge, our paper is one of the most comprehensive studies on reaction-diffusion equation-based GNNs. In our experiments with 9 datasets and 17 baselines, our method, called GREAD, outperforms them in almost all cases. Further synthetic data experiments show that GREAD mitigates the oversmoothing and performs well for various homophily rates.

Perturbation-Recovery Method for Recommendation

Collaborative filtering is one of the most influential recommender system types. Various methods have been proposed for collaborative filtering, ranging from matrix factorization to graph convolutional methods. Being inspired by recent successes of GF-CF and diffusion models, we present a novel concept of blurring-sharpening process model (BSPM). Diffusion models and BSPMs share the same processing philosophy in that new information is discovered (e.g., a new image is generated in the case of diffusion models) while original information is first perturbed and then recovered to its original form. However, diffusion models and our BSPMs deal with different types of information, and their optimal perturbation and recovery processes have a fundamental discrepancy. Therefore, our BSPMs have different forms from diffusion models. In addition, our concept not only theoretically subsumes many existing collaborative filtering models but also outperforms them in terms of Recall and NDCG in the three benchmark datasets, Gowalla, Yelp2018, and Amazon-book. Our model marks the best accuracy in them. In addition, the processing time of our method is one of the shortest cases ever in collaborative filtering. Our proposed concept has much potential in the future to be enhanced by designing better blurring (i.e., perturbation) and sharpening (i.e., recovery) processes than what we use in this paper.

TimeKit: A Time-series Forecasting-based Upgrade Kit for Collaborative Filtering

Recommender systems are a long-standing research problem in data mining and machine learning. They are incremental in nature, as new user-item interaction logs arrive. In real-world applications, we need to periodically train a collaborative filtering algorithm to extract user/item embedding vectors and therefore, a time-series of embedding vectors can be naturally defined. We present a time-series forecasting-based upgrade kit (TimeKit), which works in the following way: it i) first decides a base collaborative filtering algorithm, ii) extracts user/item embedding vectors with the base algorithm from user-item interaction logs incrementally, e.g., every month, iii) trains our time-series forecasting model with the extracted time-series of embedding vectors, and then iv) forecasts the future embedding vectors and recommend with their dot-product scores owing to a recent breakthrough in processing complicated time-series data, i.e., neural controlled differential equations (NCDEs). Our experiments with four real-world benchmark datasets show that the proposed time-series forecasting-based upgrade kit can significantly enhance existing popular collaborative filtering algorithms.

Prediction-based One-shot Dynamic Parking Pricing

Many U.S. metropolitan cities are notorious for their severe shortage of parking spots. To this end, we present a proactive prediction-driven optimization framework to dynamically adjust parking prices. We use state-of-the-art deep learning technologies such as neural ordinary differential equations (NODEs) to design our future parking occupancy rate prediction model given historical occupancy rates and price information. Owing to the continuous and bijective characteristics of NODEs, in addition, we design a one-shot price optimization method given a pre-trained prediction model, which requires only one iteration to find the optimal solution. In other words, we optimize the price input to the pre-trained prediction model to achieve targeted occupancy rates in the parking blocks. We conduct experiments with the data collected in San Francisco and Seattle for years. Our prediction model shows the best accuracy in comparison with various temporal or spatio-temporal forecasting models. Our one-shot optimization method greatly outperforms other black-box and white-box search methods in terms of the search time and always returns the optimal price solution.

Attentive Neural Controlled Differential Equations for Time-series Classification and Forecasting

Neural networks inspired by differential equations have proliferated for the past several years. Neural ordinary differential equations (NODEs) and neural controlled differential equations (NCDEs) are two representative examples of them. In theory, NCDEs provide better representation learning capability for time-series data than NODEs. In particular, it is known that NCDEs are suitable for processing irregular time-series data. Whereas NODEs have been successfully extended after adopting attention, however, it had not been studied yet how to integrate attention into NCDEs. To this end, we present the method of Attentive Neural Controlled Differential Equations (ANCDEs) for time-series classification and forecasting, where dual NCDEs are used: one for generating attention values, and the other for evolving hidden vectors for a downstream machine learning task. We conduct experiments with three real-world time-series datasets and 10 baselines. After dropping some values, we also conduct irregular time-series experiments. Our method consistently shows the best accuracy in all cases by non-trivial margins. Our visualizations also show that the presented attention mechanism works as intended by focusing on crucial information.

Large-Scale Data-Driven Airline Market Influence Maximization

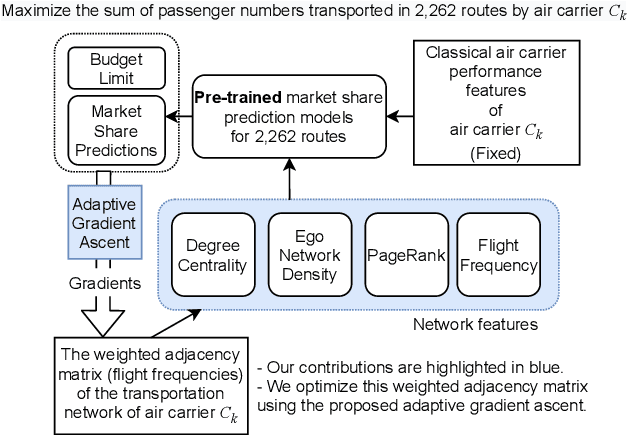
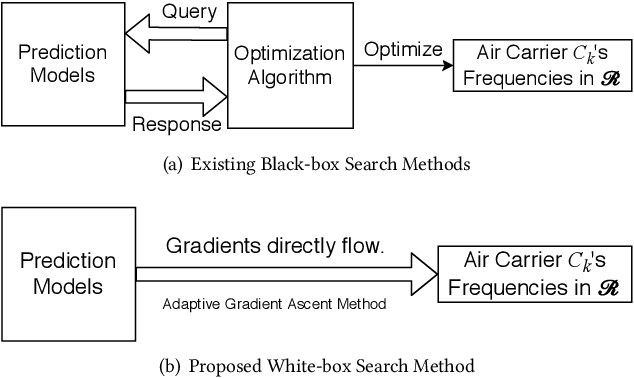
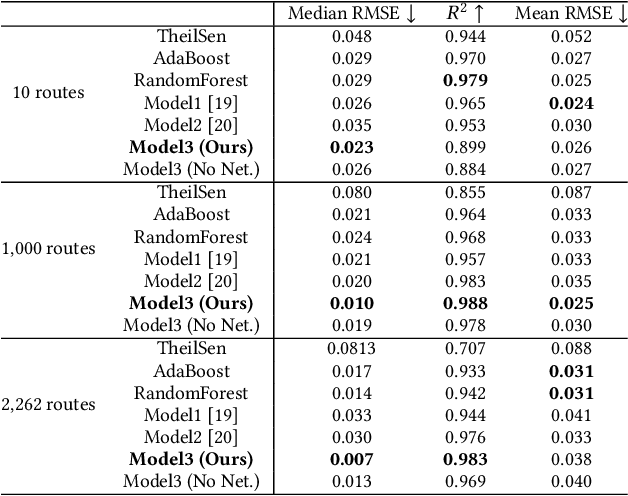
We present a prediction-driven optimization framework to maximize the market influence in the US domestic air passenger transportation market by adjusting flight frequencies. At the lower level, our neural networks consider a wide variety of features, such as classical air carrier performance features and transportation network features, to predict the market influence. On top of the prediction models, we define a budget-constrained flight frequency optimization problem to maximize the market influence over 2,262 routes. This problem falls into the category of the non-linear optimization problem, which cannot be solved exactly by conventional methods. To this end, we present a novel adaptive gradient ascent (AGA) method. Our prediction models show two to eleven times better accuracy in terms of the median root-mean-square error (RMSE) over baselines. In addition, our AGA optimization method runs 690 times faster with a better optimization result (in one of our largest scale experiments) than a greedy algorithm.