PIG: Physics-Informed Gaussians as Adaptive Parametric Mesh Representations

The approximation of Partial Differential Equations (PDEs) using neural networks has seen significant advancements through Physics-Informed Neural Networks (PINNs). Despite their straightforward optimization framework and flexibility in implementing various PDEs, PINNs often suffer from limited accuracy due to the spectral bias of Multi-Layer Perceptrons (MLPs), which struggle to effectively learn high-frequency and non-linear components. Recently, parametric mesh representations in combination with neural networks have been investigated as a promising approach to eliminate the inductive biases of neural networks. However, they usually require very high-resolution grids and a large number of collocation points to achieve high accuracy while avoiding overfitting issues. In addition, the fixed positions of the mesh parameters restrict their flexibility, making it challenging to accurately approximate complex PDEs. To overcome these limitations, we propose Physics-Informed Gaussians (PIGs), which combine feature embeddings using Gaussian functions with a lightweight neural network. Our approach uses trainable parameters for the mean and variance of each Gaussian, allowing for dynamic adjustment of their positions and shapes during training. This adaptability enables our model to optimally approximate PDE solutions, unlike models with fixed parameter positions. Furthermore, the proposed approach maintains the same optimization framework used in PINNs, allowing us to benefit from their excellent properties. Experimental results show the competitive performance of our model across various PDEs, demonstrating its potential as a robust tool for solving complex PDEs. Our project page is available at https://namgyukang.github.io/Physics-Informed-Gaussians/

Constant Acceleration Flow

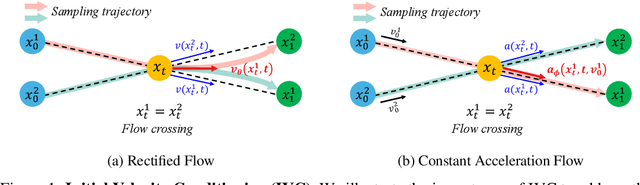
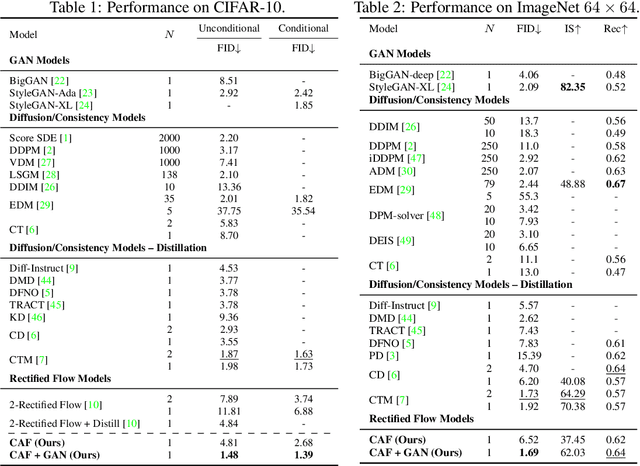
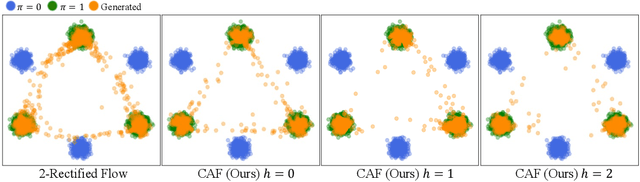
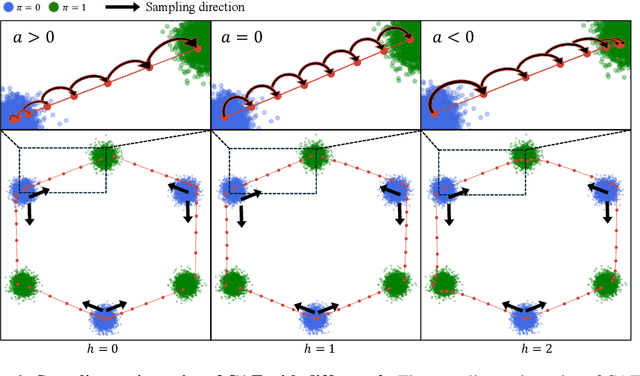
Rectified flow and reflow procedures have significantly advanced fast generation by progressively straightening ordinary differential equation (ODE) flows. They operate under the assumption that image and noise pairs, known as couplings, can be approximated by straight trajectories with constant velocity. However, we observe that modeling with constant velocity and using reflow procedures have limitations in accurately learning straight trajectories between pairs, resulting in suboptimal performance in few-step generation. To address these limitations, we introduce Constant Acceleration Flow (CAF), a novel framework based on a simple constant acceleration equation. CAF introduces acceleration as an additional learnable variable, allowing for more expressive and accurate estimation of the ODE flow. Moreover, we propose two techniques to further improve estimation accuracy: initial velocity conditioning for the acceleration model and a reflow process for the initial velocity. Our comprehensive studies on toy datasets, CIFAR-10, and ImageNet 64x64 demonstrate that CAF outperforms state-of-the-art baselines for one-step generation. We also show that CAF dramatically improves few-step coupling preservation and inversion over Rectified flow. Code is available at \href{https://github.com/mlvlab/CAF}{https://github.com/mlvlab/CAF}.

MaD-Scientist: AI-based Scientist solving Convection-Diffusion-Reaction Equations Using Massive PINN-Based Prior Data

Large language models (LLMs), like ChatGPT, have shown that even trained with noisy prior data, they can generalize effectively to new tasks through in-context learning (ICL) and pre-training techniques. Motivated by this, we explore whether a similar approach can be applied to scientific foundation models (SFMs). Our methodology is structured as follows: (i) we collect low-cost physics-informed neural network (PINN)-based approximated prior data in the form of solutions to partial differential equations (PDEs) constructed through an arbitrary linear combination of mathematical dictionaries; (ii) we utilize Transformer architectures with self and cross-attention mechanisms to predict PDE solutions without knowledge of the governing equations in a zero-shot setting; (iii) we provide experimental evidence on the one-dimensional convection-diffusion-reaction equation, which demonstrate that pre-training remains robust even with approximated prior data, with only marginal impacts on test accuracy. Notably, this finding opens the path to pre-training SFMs with realistic, low-cost data instead of (or in conjunction with) numerical high-cost data. These results support the conjecture that SFMs can improve in a manner similar to LLMs, where fully cleaning the vast set of sentences crawled from the Internet is nearly impossible.

Error analysis for finite element operator learning methods for solving parametric second-order elliptic PDEs

In this paper, we provide a theoretical analysis of a type of operator learning method without data reliance based on the classical finite element approximation, which is called the finite element operator network (FEONet). We first establish the convergence of this method for general second-order linear elliptic PDEs with respect to the parameters for neural network approximation. In this regard, we address the role of the condition number of the finite element matrix in the convergence of the method. Secondly, we derive an explicit error estimate for the self-adjoint case. For this, we investigate some regularity properties of the solution in certain function classes for a neural network approximation, verifying the sufficient condition for the solution to have the desired regularity. Finally, we will also conduct some numerical experiments that support the theoretical findings, confirming the role of the condition number of the finite element matrix in the overall convergence.

Separable Physics-informed Neural Networks for Solving the BGK Model of the Boltzmann Equation

In this study, we introduce a method based on Separable Physics-Informed Neural Networks (SPINNs) for effectively solving the BGK model of the Boltzmann equation. While the mesh-free nature of PINNs offers significant advantages in handling high-dimensional partial differential equations (PDEs), challenges arise when applying quadrature rules for accurate integral evaluation in the BGK operator, which can compromise the mesh-free benefit and increase computational costs. To address this, we leverage the canonical polyadic decomposition structure of SPINNs and the linear nature of moment calculation, achieving a substantial reduction in computational expense for quadrature rule application. The multi-scale nature of the particle density function poses difficulties in precisely approximating macroscopic moments using neural networks. To improve SPINN training, we introduce the integration of Gaussian functions into SPINNs, coupled with a relative loss approach. This modification enables SPINNs to decay as rapidly as Maxwellian distributions, thereby enhancing the accuracy of macroscopic moment approximations. The relative loss design further ensures that both large and small-scale features are effectively captured by the SPINNs. The efficacy of our approach is demonstrated through a series of five numerical experiments, including the solution to a challenging 3D Riemann problem. These results highlight the potential of our novel method in efficiently and accurately addressing complex challenges in computational physics.

Spectral operator learning for parametric PDEs without data reliance

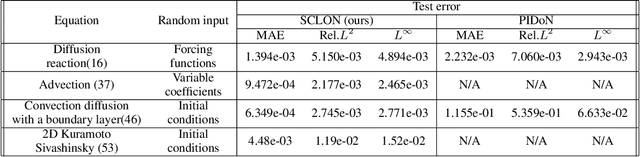
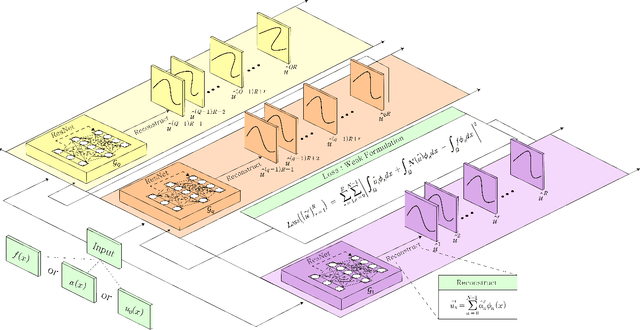
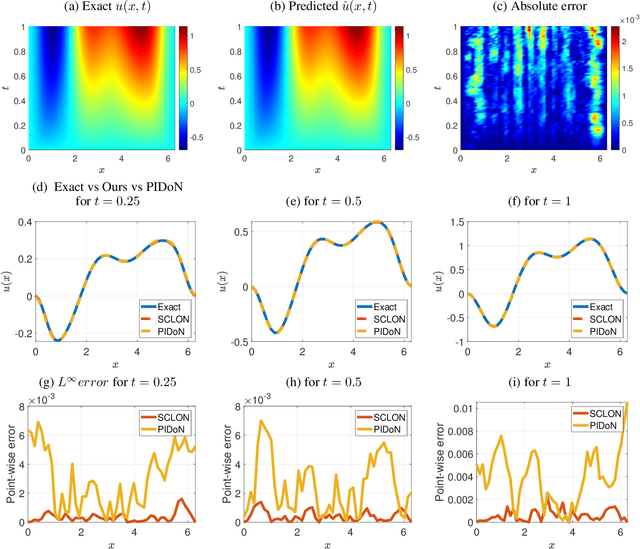
In this paper, we introduce the Spectral Coefficient Learning via Operator Network (SCLON), a novel operator learning-based approach for solving parametric partial differential equations (PDEs) without the need for data harnessing. The cornerstone of our method is the spectral methodology that employs expansions using orthogonal functions, such as Fourier series and Legendre polynomials, enabling accurate PDE solutions with fewer grid points. By merging the merits of spectral methods - encompassing high accuracy, efficiency, generalization, and the exact fulfillment of boundary conditions - with the prowess of deep neural networks, SCLON offers a transformative strategy. Our approach not only eliminates the need for paired input-output training data, which typically requires extensive numerical computations, but also effectively learns and predicts solutions of complex parametric PDEs, ranging from singularly perturbed convection-diffusion equations to the Navier-Stokes equations. The proposed framework demonstrates superior performance compared to existing scientific machine learning techniques, offering solutions for multiple instances of parametric PDEs without harnessing data. The mathematical framework is robust and reliable, with a well-developed loss function derived from the weak formulation, ensuring accurate approximation of solutions while exactly satisfying boundary conditions. The method's efficacy is further illustrated through its ability to accurately predict intricate natural behaviors like the Kolmogorov flow and boundary layers. In essence, our work pioneers a compelling avenue for parametric PDE solutions, serving as a bridge between traditional numerical methodologies and cutting-edge machine learning techniques in the realm of scientific computation.

Hydra: Multi-head Low-rank Adaptation for Parameter Efficient Fine-tuning

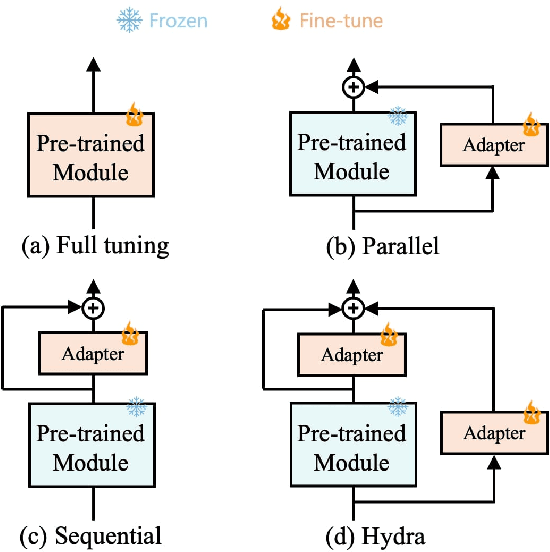
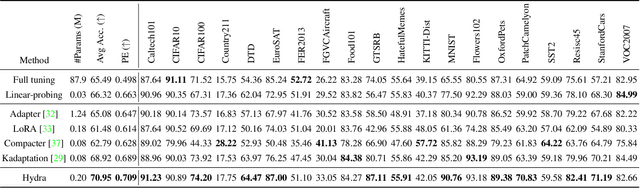
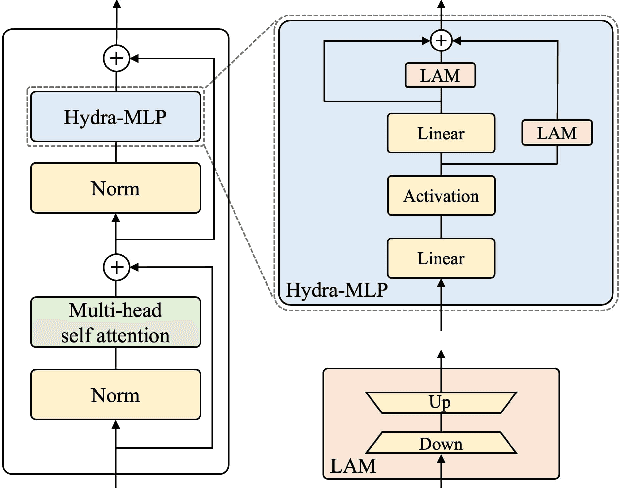
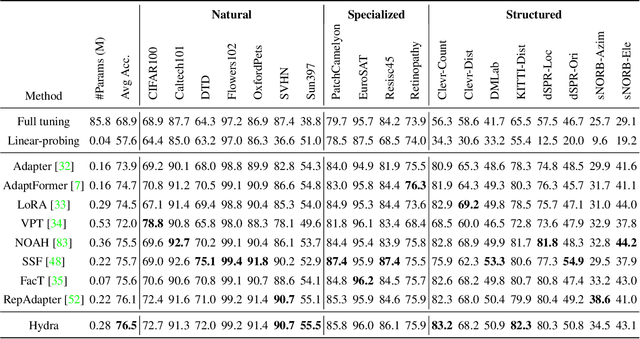
The recent surge in large-scale foundation models has spurred the development of efficient methods for adapting these models to various downstream tasks. Low-rank adaptation methods, such as LoRA, have gained significant attention due to their outstanding parameter efficiency and no additional inference latency. This paper investigates a more general form of adapter module based on the analysis that parallel and sequential adaptation branches learn novel and general features during fine-tuning, respectively. The proposed method, named Hydra, due to its multi-head computational branches, combines parallel and sequential branch to integrate capabilities, which is more expressive than existing single branch methods and enables the exploration of a broader range of optimal points in the fine-tuning process. In addition, the proposed adaptation method explicitly leverages the pre-trained weights by performing a linear combination of the pre-trained features. It allows the learned features to have better generalization performance across diverse downstream tasks. Furthermore, we perform a comprehensive analysis of the characteristics of each adaptation branch with empirical evidence. Through an extensive range of experiments, encompassing comparisons and ablation studies, we substantiate the efficiency and demonstrate the superior performance of Hydra. This comprehensive evaluation underscores the potential impact and effectiveness of Hydra in a variety of applications. Our code is available on \url{https://github.com/extremebird/Hydra}

Finite Element Operator Network for Solving Parametric PDEs

Partial differential equations (PDEs) underlie our understanding and prediction of natural phenomena across numerous fields, including physics, engineering, and finance. However, solving parametric PDEs is a complex task that necessitates efficient numerical methods. In this paper, we propose a novel approach for solving parametric PDEs using a Finite Element Operator Network (FEONet). Our proposed method leverages the power of deep learning in conjunction with traditional numerical methods, specifically the finite element method, to solve parametric PDEs in the absence of any paired input-output training data. We demonstrate the effectiveness of our approach on several benchmark problems and show that it outperforms existing state-of-the-art methods in terms of accuracy, generalization, and computational flexibility. Our FEONet framework shows potential for application in various fields where PDEs play a crucial role in modeling complex domains with diverse boundary conditions and singular behavior. Furthermore, we provide theoretical convergence analysis to support our approach, utilizing finite element approximation in numerical analysis.

Separable Physics-Informed Neural Networks

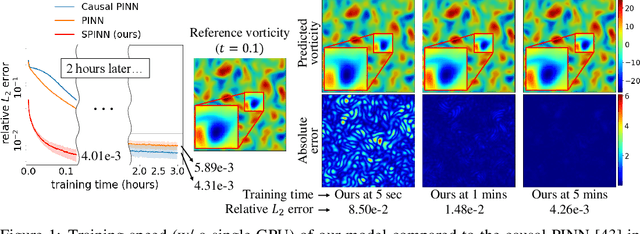
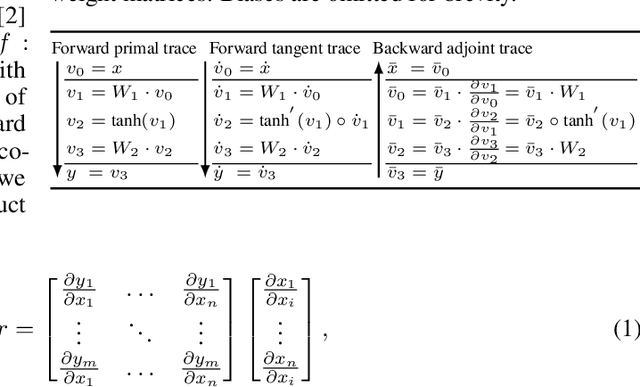
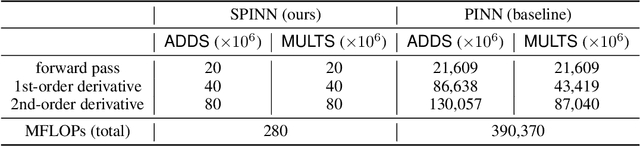
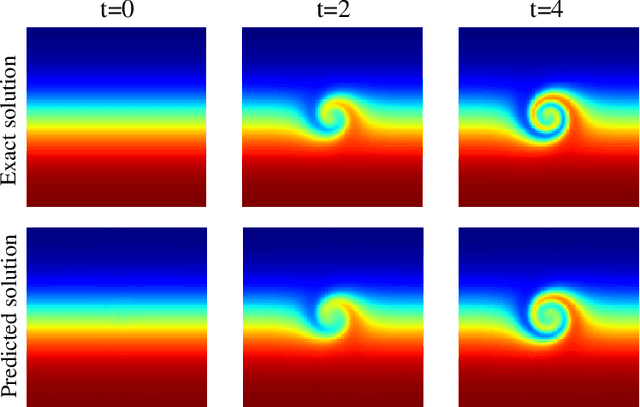
Physics-informed neural networks (PINNs) have recently emerged as promising data-driven PDE solvers showing encouraging results on various PDEs. However, there is a fundamental limitation of training PINNs to solve multi-dimensional PDEs and approximate highly complex solution functions. The number of training points (collocation points) required on these challenging PDEs grows substantially, but it is severely limited due to the expensive computational costs and heavy memory overhead. To overcome this issue, we propose a network architecture and training algorithm for PINNs. The proposed method, separable PINN (SPINN), operates on a per-axis basis to significantly reduce the number of network propagations in multi-dimensional PDEs unlike point-wise processing in conventional PINNs. We also propose using forward-mode automatic differentiation to reduce the computational cost of computing PDE residuals, enabling a large number of collocation points (>10^7) on a single commodity GPU. The experimental results show drastically reduced computational costs (62x in wall-clock time, 1,394x in FLOPs given the same number of collocation points) in multi-dimensional PDEs while achieving better accuracy. Furthermore, we present that SPINN can solve a chaotic (2+1)-d Navier-Stokes equation significantly faster than the best-performing prior method (9 minutes vs 10 hours in a single GPU), maintaining accuracy. Finally, we showcase that SPINN can accurately obtain the solution of a highly nonlinear and multi-dimensional PDE, a (3+1)-d Navier-Stokes equation. For visualized results and code, please see https://jwcho5576.github.io/spinn.github.io/.

Separable PINN: Mitigating the Curse of Dimensionality in Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have emerged as new data-driven PDE solvers for both forward and inverse problems. While promising, the expensive computational costs to obtain solutions often restrict their broader applicability. We demonstrate that the computations in automatic differentiation (AD) can be significantly reduced by leveraging forward-mode AD when training PINN. However, a naive application of forward-mode AD to conventional PINNs results in higher computation, losing its practical benefit. Therefore, we propose a network architecture, called separable PINN (SPINN), which can facilitate forward-mode AD for more efficient computation. SPINN operates on a per-axis basis instead of point-wise processing in conventional PINNs, decreasing the number of network forward passes. Besides, while the computation and memory costs of standard PINNs grow exponentially along with the grid resolution, that of our model is remarkably less susceptible, mitigating the curse of dimensionality. We demonstrate the effectiveness of our model in various PDE systems by significantly reducing the training run-time while achieving comparable accuracy. Project page: https://jwcho5576.github.io/spinn/