Separable Physics-Informed Neural Networks

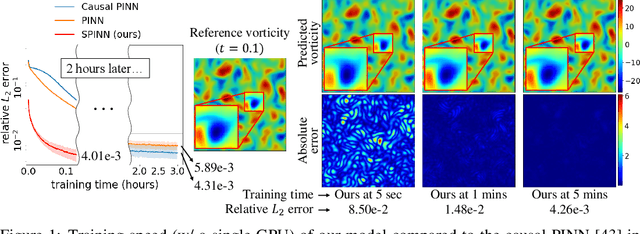
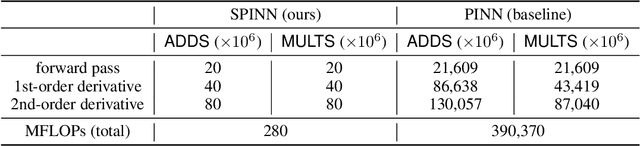
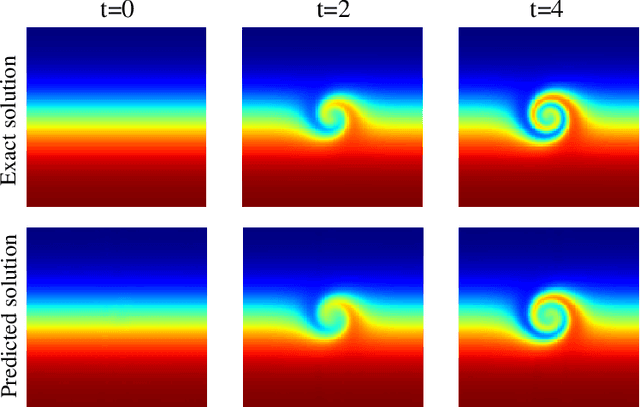
Physics-informed neural networks (PINNs) have recently emerged as promising data-driven PDE solvers showing encouraging results on various PDEs. However, there is a fundamental limitation of training PINNs to solve multi-dimensional PDEs and approximate highly complex solution functions. The number of training points (collocation points) required on these challenging PDEs grows substantially, but it is severely limited due to the expensive computational costs and heavy memory overhead. To overcome this issue, we propose a network architecture and training algorithm for PINNs. The proposed method, separable PINN (SPINN), operates on a per-axis basis to significantly reduce the number of network propagations in multi-dimensional PDEs unlike point-wise processing in conventional PINNs. We also propose using forward-mode automatic differentiation to reduce the computational cost of computing PDE residuals, enabling a large number of collocation points (>10^7) on a single commodity GPU. The experimental results show drastically reduced computational costs (62x in wall-clock time, 1,394x in FLOPs given the same number of collocation points) in multi-dimensional PDEs while achieving better accuracy. Furthermore, we present that SPINN can solve a chaotic (2+1)-d Navier-Stokes equation significantly faster than the best-performing prior method (9 minutes vs 10 hours in a single GPU), maintaining accuracy. Finally, we showcase that SPINN can accurately obtain the solution of a highly nonlinear and multi-dimensional PDE, a (3+1)-d Navier-Stokes equation. For visualized results and code, please see https://jwcho5576.github.io/spinn.github.io/.

Separable PINN: Mitigating the Curse of Dimensionality in Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have emerged as new data-driven PDE solvers for both forward and inverse problems. While promising, the expensive computational costs to obtain solutions often restrict their broader applicability. We demonstrate that the computations in automatic differentiation (AD) can be significantly reduced by leveraging forward-mode AD when training PINN. However, a naive application of forward-mode AD to conventional PINNs results in higher computation, losing its practical benefit. Therefore, we propose a network architecture, called separable PINN (SPINN), which can facilitate forward-mode AD for more efficient computation. SPINN operates on a per-axis basis instead of point-wise processing in conventional PINNs, decreasing the number of network forward passes. Besides, while the computation and memory costs of standard PINNs grow exponentially along with the grid resolution, that of our model is remarkably less susceptible, mitigating the curse of dimensionality. We demonstrate the effectiveness of our model in various PDE systems by significantly reducing the training run-time while achieving comparable accuracy. Project page: https://jwcho5576.github.io/spinn/

Streamable Neural Fields

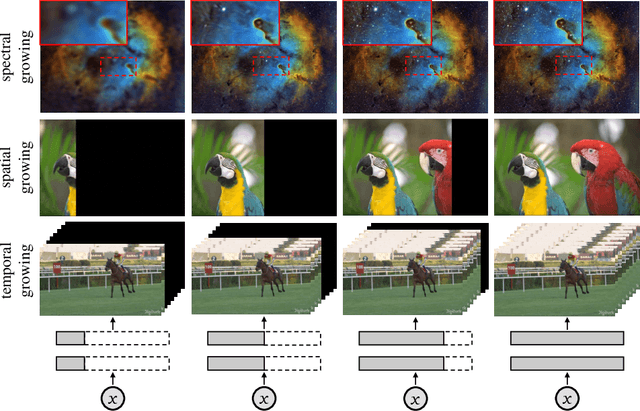
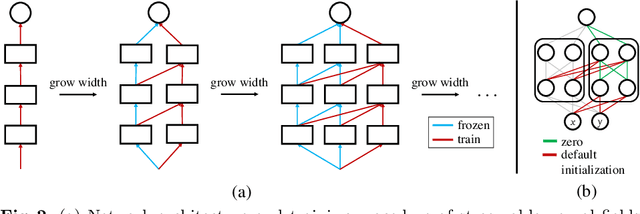
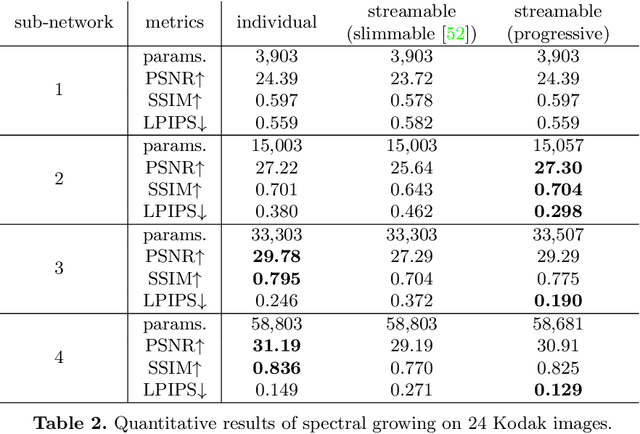
Neural fields have emerged as a new data representation paradigm and have shown remarkable success in various signal representations. Since they preserve signals in their network parameters, the data transfer by sending and receiving the entire model parameters prevents this emerging technology from being used in many practical scenarios. We propose streamable neural fields, a single model that consists of executable sub-networks of various widths. The proposed architectural and training techniques enable a single network to be streamable over time and reconstruct different qualities and parts of signals. For example, a smaller sub-network produces smooth and low-frequency signals, while a larger sub-network can represent fine details. Experimental results have shown the effectiveness of our method in various domains, such as 2D images, videos, and 3D signed distance functions. Finally, we demonstrate that our proposed method improves training stability, by exploiting parameter sharing.

Neural Residual Flow Fields for Efficient Video Representations

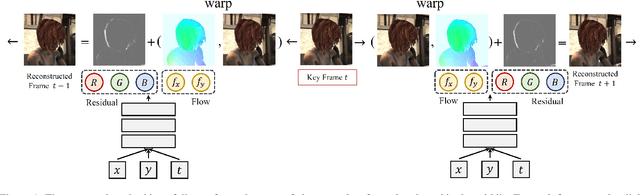
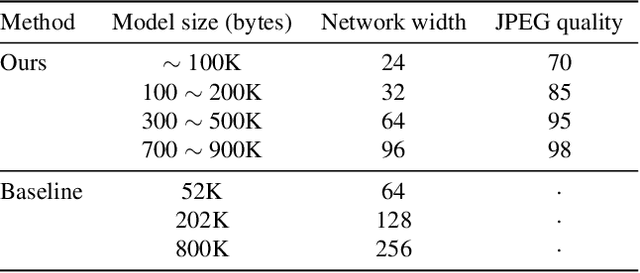
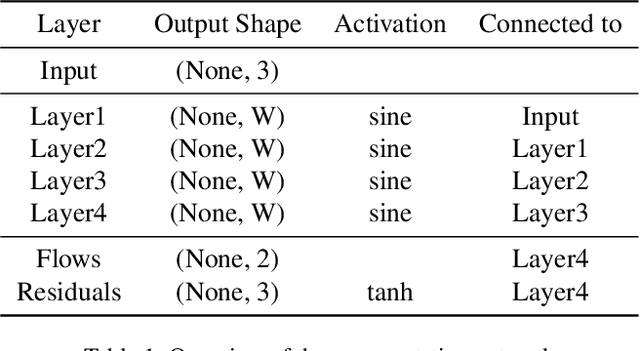
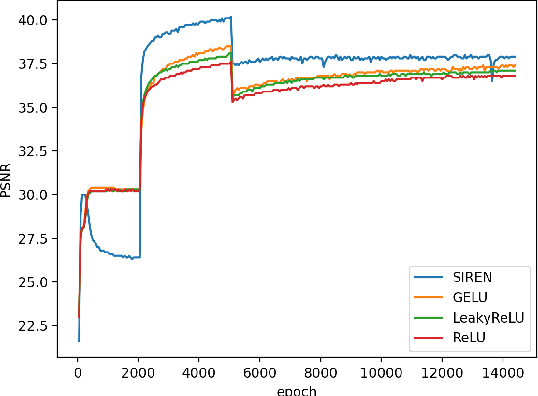
Implicit neural representation (INR) has emerged as a powerful paradigm for representing signals, such as images, videos, 3D shapes, etc. Although it has shown the ability to represent fine details, its efficiency as a data representation has not been extensively studied. In INR, the data is stored in the form of parameters of a neural network and general purpose optimization algorithms do not generally exploit the spatial and temporal redundancy in signals. In this paper, we suggest a novel INR approach to representing and compressing videos by explicitly removing data redundancy. Instead of storing raw RGB colors, we propose Neural Residual Flow Fields (NRFF), using motion information across video frames and residuals that are necessary to reconstruct a video. Maintaining the motion information, which is usually smoother and less complex than the raw signals, requires far fewer parameters. Furthermore, reusing redundant pixel values further improves the network parameter efficiency. Experimental results have shown that the proposed method outperforms the baseline methods by a significant margin. The code is available in https://github.com/daniel03c1/eff_video_representation.