Parameter-Efficient Instance-Adaptive Neural Video Compression

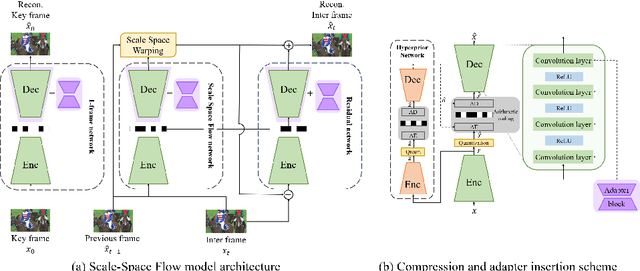
Learning-based Neural Video Codecs (NVCs) have emerged as a compelling alternative to the standard video codecs, demonstrating promising performance, and simple and easily maintainable pipelines. However, NVCs often fall short of compression performance and occasionally exhibit poor generalization capability due to inference-only compression scheme and their dependence on training data. The instance-adaptive video compression techniques have recently been suggested as a viable solution, fine-tuning the encoder or decoder networks for a particular test instance video. However, fine-tuning all the model parameters incurs high computational costs, increases the bitrates, and often leads to unstable training. In this work, we propose a parameter-efficient instance-adaptive video compression framework. Inspired by the remarkable success of parameter-efficient fine-tuning on large-scale neural network models, we propose to use a lightweight adapter module that can be easily attached to the pretrained NVCs and fine-tuned for test video sequences. The resulting algorithm significantly improves compression performance and reduces the encoding time compared to the existing instant-adaptive video compression algorithms. Furthermore, the suggested fine-tuning method enhances the robustness of the training process, allowing for the proposed method to be widely used in many practical settings. We conducted extensive experiments on various standard benchmark datasets, including UVG, MCL-JVC, and HEVC sequences, and the experimental results have shown a significant improvement in rate-distortion (RD) curves (up to 5 dB PSNR improvements) and BD rates compared to the baselines NVC.

Hydra: Multi-head Low-rank Adaptation for Parameter Efficient Fine-tuning

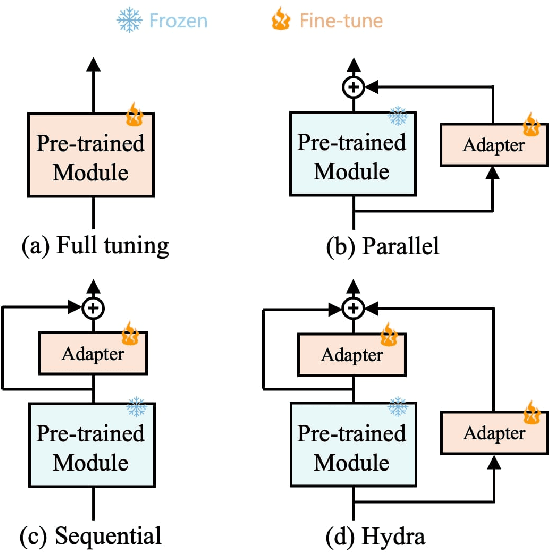
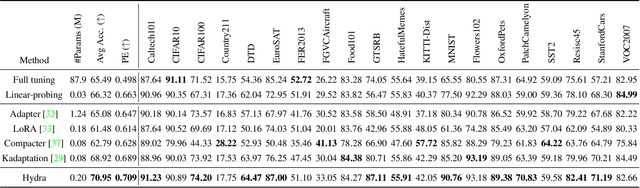
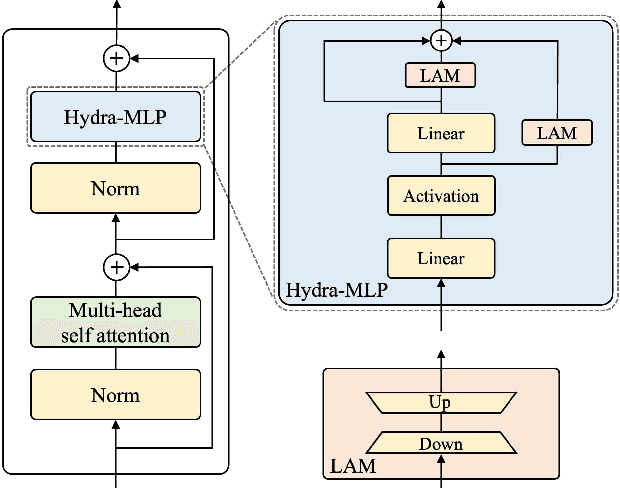
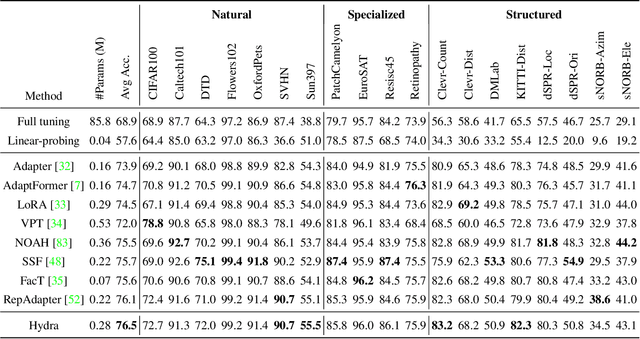
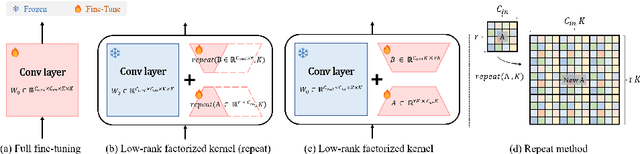
The recent surge in large-scale foundation models has spurred the development of efficient methods for adapting these models to various downstream tasks. Low-rank adaptation methods, such as LoRA, have gained significant attention due to their outstanding parameter efficiency and no additional inference latency. This paper investigates a more general form of adapter module based on the analysis that parallel and sequential adaptation branches learn novel and general features during fine-tuning, respectively. The proposed method, named Hydra, due to its multi-head computational branches, combines parallel and sequential branch to integrate capabilities, which is more expressive than existing single branch methods and enables the exploration of a broader range of optimal points in the fine-tuning process. In addition, the proposed adaptation method explicitly leverages the pre-trained weights by performing a linear combination of the pre-trained features. It allows the learned features to have better generalization performance across diverse downstream tasks. Furthermore, we perform a comprehensive analysis of the characteristics of each adaptation branch with empirical evidence. Through an extensive range of experiments, encompassing comparisons and ablation studies, we substantiate the efficiency and demonstrate the superior performance of Hydra. This comprehensive evaluation underscores the potential impact and effectiveness of Hydra in a variety of applications. Our code is available on \url{https://github.com/extremebird/Hydra}

Separable Physics-Informed Neural Networks

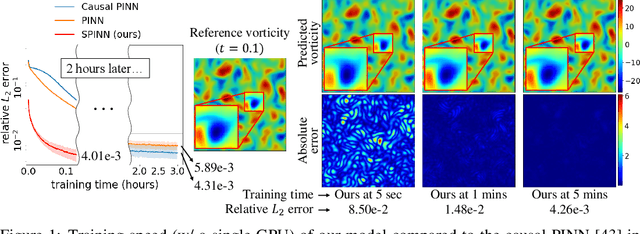
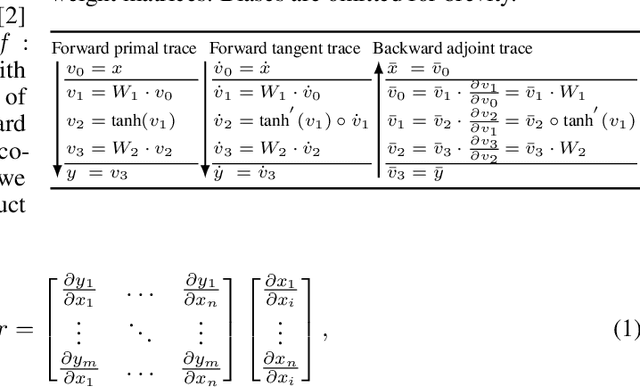
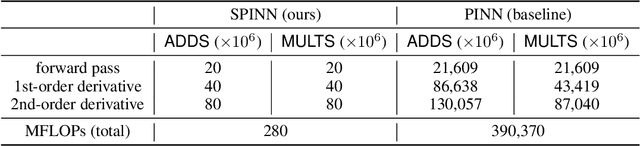
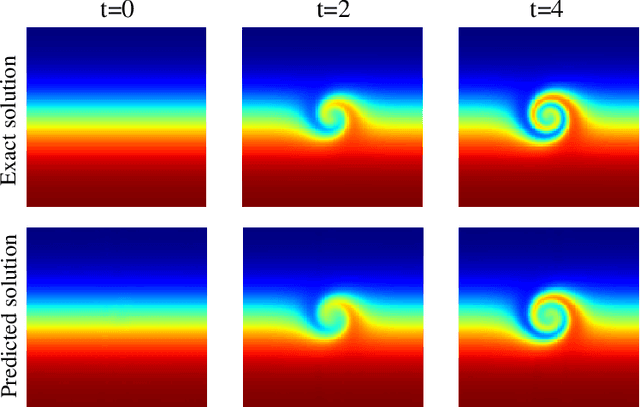
Physics-informed neural networks (PINNs) have recently emerged as promising data-driven PDE solvers showing encouraging results on various PDEs. However, there is a fundamental limitation of training PINNs to solve multi-dimensional PDEs and approximate highly complex solution functions. The number of training points (collocation points) required on these challenging PDEs grows substantially, but it is severely limited due to the expensive computational costs and heavy memory overhead. To overcome this issue, we propose a network architecture and training algorithm for PINNs. The proposed method, separable PINN (SPINN), operates on a per-axis basis to significantly reduce the number of network propagations in multi-dimensional PDEs unlike point-wise processing in conventional PINNs. We also propose using forward-mode automatic differentiation to reduce the computational cost of computing PDE residuals, enabling a large number of collocation points (>10^7) on a single commodity GPU. The experimental results show drastically reduced computational costs (62x in wall-clock time, 1,394x in FLOPs given the same number of collocation points) in multi-dimensional PDEs while achieving better accuracy. Furthermore, we present that SPINN can solve a chaotic (2+1)-d Navier-Stokes equation significantly faster than the best-performing prior method (9 minutes vs 10 hours in a single GPU), maintaining accuracy. Finally, we showcase that SPINN can accurately obtain the solution of a highly nonlinear and multi-dimensional PDE, a (3+1)-d Navier-Stokes equation. For visualized results and code, please see https://jwcho5576.github.io/spinn.github.io/.

Separable PINN: Mitigating the Curse of Dimensionality in Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have emerged as new data-driven PDE solvers for both forward and inverse problems. While promising, the expensive computational costs to obtain solutions often restrict their broader applicability. We demonstrate that the computations in automatic differentiation (AD) can be significantly reduced by leveraging forward-mode AD when training PINN. However, a naive application of forward-mode AD to conventional PINNs results in higher computation, losing its practical benefit. Therefore, we propose a network architecture, called separable PINN (SPINN), which can facilitate forward-mode AD for more efficient computation. SPINN operates on a per-axis basis instead of point-wise processing in conventional PINNs, decreasing the number of network forward passes. Besides, while the computation and memory costs of standard PINNs grow exponentially along with the grid resolution, that of our model is remarkably less susceptible, mitigating the curse of dimensionality. We demonstrate the effectiveness of our model in various PDE systems by significantly reducing the training run-time while achieving comparable accuracy. Project page: https://jwcho5576.github.io/spinn/