Generative Densification: Learning to Densify Gaussians for High-Fidelity Generalizable 3D Reconstruction

Generalized feed-forward Gaussian models have achieved significant progress in sparse-view 3D reconstruction by leveraging prior knowledge from large multi-view datasets. However, these models often struggle to represent high-frequency details due to the limited number of Gaussians. While the densification strategy used in per-scene 3D Gaussian splatting (3D-GS) optimization can be adapted to the feed-forward models, it may not be ideally suited for generalized scenarios. In this paper, we propose Generative Densification, an efficient and generalizable method to densify Gaussians generated by feed-forward models. Unlike the 3D-GS densification strategy, which iteratively splits and clones raw Gaussian parameters, our method up-samples feature representations from the feed-forward models and generates their corresponding fine Gaussians in a single forward pass, leveraging the embedded prior knowledge for enhanced generalization. Experimental results on both object-level and scene-level reconstruction tasks demonstrate that our method outperforms state-of-the-art approaches with comparable or smaller model sizes, achieving notable improvements in representing fine details.

SelfSplat: Pose-Free and 3D Prior-Free Generalizable 3D Gaussian Splatting

We propose SelfSplat, a novel 3D Gaussian Splatting model designed to perform pose-free and 3D prior-free generalizable 3D reconstruction from unposed multi-view images. These settings are inherently ill-posed due to the lack of ground-truth data, learned geometric information, and the need to achieve accurate 3D reconstruction without finetuning, making it difficult for conventional methods to achieve high-quality results. Our model addresses these challenges by effectively integrating explicit 3D representations with self-supervised depth and pose estimation techniques, resulting in reciprocal improvements in both pose accuracy and 3D reconstruction quality. Furthermore, we incorporate a matching-aware pose estimation network and a depth refinement module to enhance geometry consistency across views, ensuring more accurate and stable 3D reconstructions. To present the performance of our method, we evaluated it on large-scale real-world datasets, including RealEstate10K, ACID, and DL3DV. SelfSplat achieves superior results over previous state-of-the-art methods in both appearance and geometry quality, also demonstrates strong cross-dataset generalization capabilities. Extensive ablation studies and analysis also validate the effectiveness of our proposed methods. Code and pretrained models are available at https://gynjn.github.io/selfsplat/

Freq-Mip-AA : Frequency Mip Representation for Anti-Aliasing Neural Radiance Fields

Neural Radiance Fields (NeRF) have shown remarkable success in representing 3D scenes and generating novel views. However, they often struggle with aliasing artifacts, especially when rendering images from different camera distances from the training views. To address the issue, Mip-NeRF proposed using volumetric frustums to render a pixel and suggested integrated positional encoding (IPE). While effective, this approach requires long training times due to its reliance on MLP architecture. In this work, we propose a novel anti-aliasing technique that utilizes grid-based representations, usually showing significantly faster training time. In addition, we exploit frequency-domain representation to handle the aliasing problem inspired by the sampling theorem. The proposed method, FreqMipAA, utilizes scale-specific low-pass filtering (LPF) and learnable frequency masks. Scale-specific low-pass filters (LPF) prevent aliasing and prioritize important image details, and learnable masks effectively remove problematic high-frequency elements while retaining essential information. By employing a scale-specific LPF and trainable masks, FreqMipAA can effectively eliminate the aliasing factor while retaining important details. We validated the proposed technique by incorporating it into a widely used grid-based method. The experimental results have shown that the FreqMipAA effectively resolved the aliasing issues and achieved state-of-the-art results in the multi-scale Blender dataset. Our code is available at https://github.com/yi0109/FreqMipAA .

Mip-Grid: Anti-aliased Grid Representations for Neural Radiance Fields

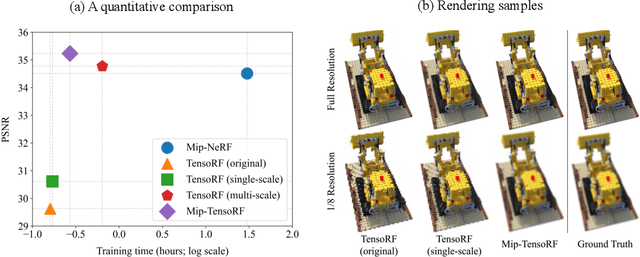
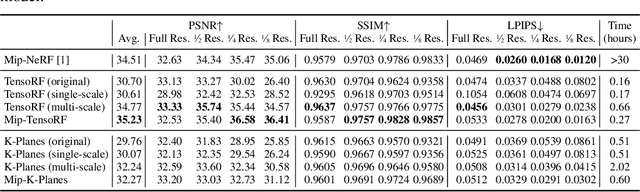
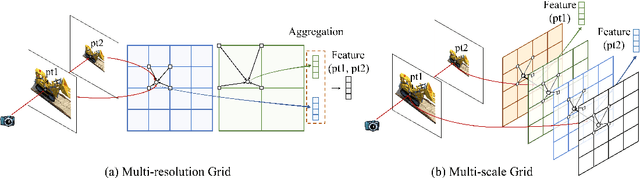
Despite the remarkable achievements of neural radiance fields (NeRF) in representing 3D scenes and generating novel view images, the aliasing issue, rendering "jaggies" or "blurry" images at varying camera distances, remains unresolved in most existing approaches. The recently proposed mip-NeRF has addressed this challenge by rendering conical frustums instead of rays. However, it relies on MLP architecture to represent the radiance fields, missing out on the fast training speed offered by the latest grid-based methods. In this work, we present mip-Grid, a novel approach that integrates anti-aliasing techniques into grid-based representations for radiance fields, mitigating the aliasing artifacts while enjoying fast training time. The proposed method generates multi-scale grids by applying simple convolution operations over a shared grid representation and uses the scale-aware coordinate to retrieve features at different scales from the generated multi-scale grids. To test the effectiveness, we integrated the proposed method into the two recent representative grid-based methods, TensoRF and K-Planes. Experimental results demonstrate that mip-Grid greatly improves the rendering performance of both methods and even outperforms mip-NeRF on multi-scale datasets while achieving significantly faster training time. For code and demo videos, please see https://stnamjef.github.io/mipgrid.github.io/.

Coordinate-Aware Modulation for Neural Fields

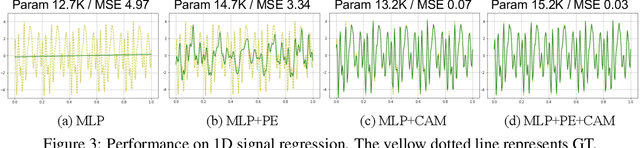
Neural fields, mapping low-dimensional input coordinates to corresponding signals, have shown promising results in representing various signals. Numerous methodologies have been proposed, and techniques employing MLPs and grid representations have achieved substantial success. MLPs allow compact and high expressibility, yet often suffer from spectral bias and slow convergence speed. On the other hand, methods using grids are free from spectral bias and achieve fast training speed, however, at the expense of high spatial complexity. In this work, we propose a novel way for exploiting both MLPs and grid representations in neural fields. Unlike the prevalent methods that combine them sequentially (extract features from the grids first and feed them to the MLP), we inject spectral bias-free grid representations into the intermediate features in the MLP. More specifically, we suggest a Coordinate-Aware Modulation (CAM), which modulates the intermediate features using scale and shift parameters extracted from the grid representations. This can maintain the strengths of MLPs while mitigating any remaining potential biases, facilitating the rapid learning of high-frequency components. In addition, we empirically found that the feature normalizations, which have not been successful in neural filed literature, proved to be effective when applied in conjunction with the proposed CAM. Experimental results demonstrate that CAM enhances the performance of neural representation and improves learning stability across a range of signals. Especially in the novel view synthesis task, we achieved state-of-the-art performance with the least number of parameters and fast training speed for dynamic scenes and the best performance under 1MB memory for static scenes. CAM also outperforms the best-performing video compression methods using neural fields by a large margin.

Separable Physics-Informed Neural Networks

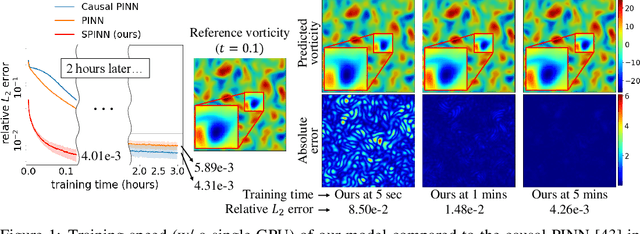
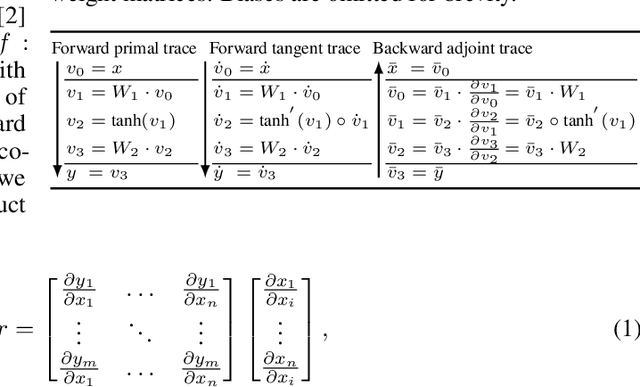
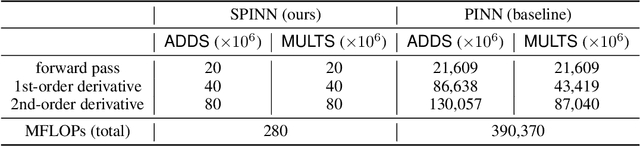
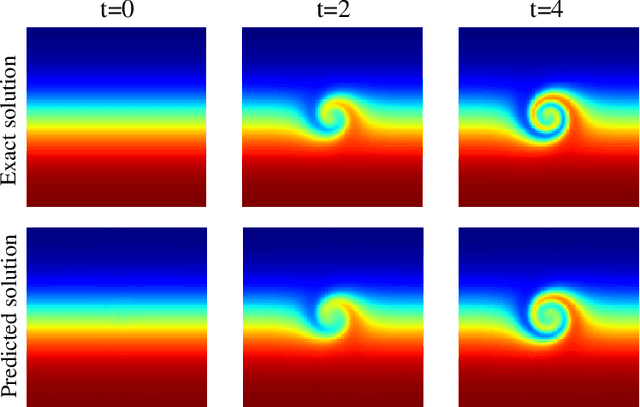
Physics-informed neural networks (PINNs) have recently emerged as promising data-driven PDE solvers showing encouraging results on various PDEs. However, there is a fundamental limitation of training PINNs to solve multi-dimensional PDEs and approximate highly complex solution functions. The number of training points (collocation points) required on these challenging PDEs grows substantially, but it is severely limited due to the expensive computational costs and heavy memory overhead. To overcome this issue, we propose a network architecture and training algorithm for PINNs. The proposed method, separable PINN (SPINN), operates on a per-axis basis to significantly reduce the number of network propagations in multi-dimensional PDEs unlike point-wise processing in conventional PINNs. We also propose using forward-mode automatic differentiation to reduce the computational cost of computing PDE residuals, enabling a large number of collocation points (>10^7) on a single commodity GPU. The experimental results show drastically reduced computational costs (62x in wall-clock time, 1,394x in FLOPs given the same number of collocation points) in multi-dimensional PDEs while achieving better accuracy. Furthermore, we present that SPINN can solve a chaotic (2+1)-d Navier-Stokes equation significantly faster than the best-performing prior method (9 minutes vs 10 hours in a single GPU), maintaining accuracy. Finally, we showcase that SPINN can accurately obtain the solution of a highly nonlinear and multi-dimensional PDE, a (3+1)-d Navier-Stokes equation. For visualized results and code, please see https://jwcho5576.github.io/spinn.github.io/.

Masked Wavelet Representation for Compact Neural Radiance Fields

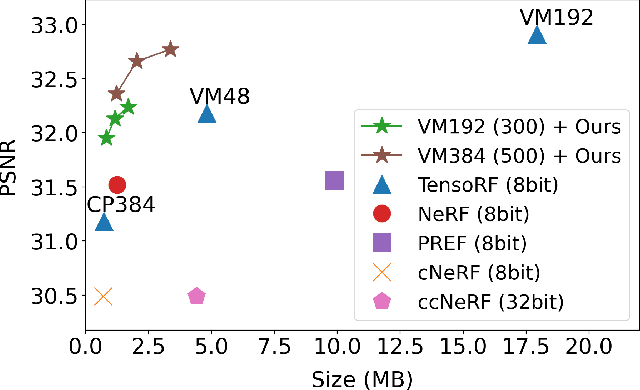
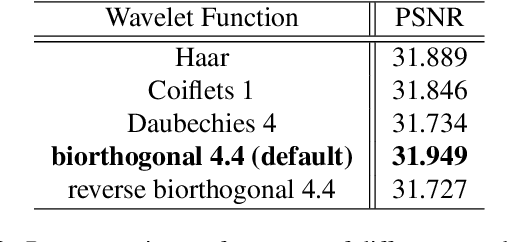
Neural radiance fields (NeRF) have demonstrated the potential of coordinate-based neural representation (neural fields or implicit neural representation) in neural rendering. However, using a multi-layer perceptron (MLP) to represent a 3D scene or object requires enormous computational resources and time. There have been recent studies on how to reduce these computational inefficiencies by using additional data structures, such as grids or trees. Despite the promising performance, the explicit data structure necessitates a substantial amount of memory. In this work, we present a method to reduce the size without compromising the advantages of having additional data structures. In detail, we propose using the wavelet transform on grid-based neural fields. Grid-based neural fields are for fast convergence, and the wavelet transform, whose efficiency has been demonstrated in high-performance standard codecs, is to improve the parameter efficiency of grids. Furthermore, in order to achieve a higher sparsity of grid coefficients while maintaining reconstruction quality, we present a novel trainable masking approach. Experimental results demonstrate that non-spatial grid coefficients, such as wavelet coefficients, are capable of attaining a higher level of sparsity than spatial grid coefficients, resulting in a more compact representation. With our proposed mask and compression pipeline, we achieved state-of-the-art performance within a memory budget of 2 MB. Our code is available at https://github.com/daniel03c1/masked_wavelet_nerf.

Separable PINN: Mitigating the Curse of Dimensionality in Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have emerged as new data-driven PDE solvers for both forward and inverse problems. While promising, the expensive computational costs to obtain solutions often restrict their broader applicability. We demonstrate that the computations in automatic differentiation (AD) can be significantly reduced by leveraging forward-mode AD when training PINN. However, a naive application of forward-mode AD to conventional PINNs results in higher computation, losing its practical benefit. Therefore, we propose a network architecture, called separable PINN (SPINN), which can facilitate forward-mode AD for more efficient computation. SPINN operates on a per-axis basis instead of point-wise processing in conventional PINNs, decreasing the number of network forward passes. Besides, while the computation and memory costs of standard PINNs grow exponentially along with the grid resolution, that of our model is remarkably less susceptible, mitigating the curse of dimensionality. We demonstrate the effectiveness of our model in various PDE systems by significantly reducing the training run-time while achieving comparable accuracy. Project page: https://jwcho5576.github.io/spinn/

Streamable Neural Fields

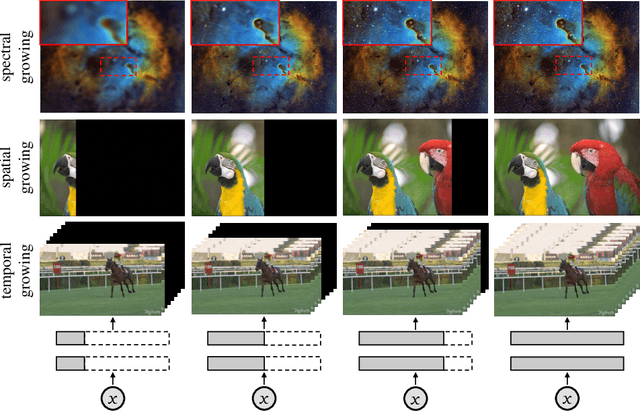
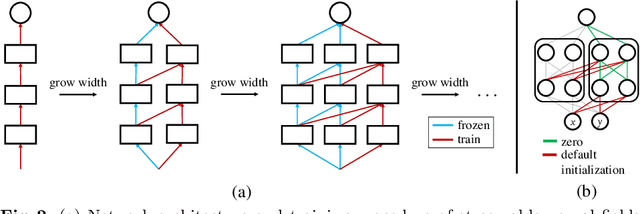
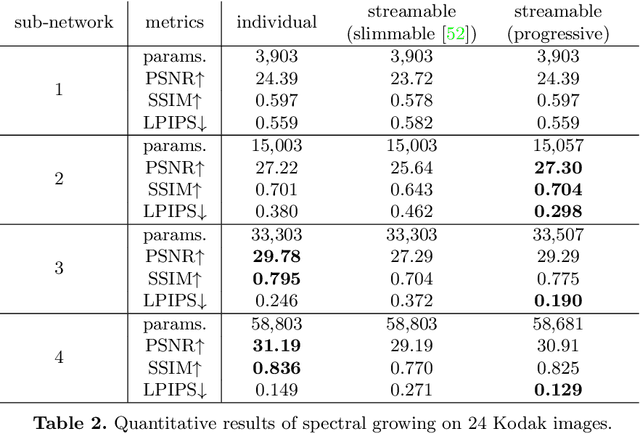
Neural fields have emerged as a new data representation paradigm and have shown remarkable success in various signal representations. Since they preserve signals in their network parameters, the data transfer by sending and receiving the entire model parameters prevents this emerging technology from being used in many practical scenarios. We propose streamable neural fields, a single model that consists of executable sub-networks of various widths. The proposed architectural and training techniques enable a single network to be streamable over time and reconstruct different qualities and parts of signals. For example, a smaller sub-network produces smooth and low-frequency signals, while a larger sub-network can represent fine details. Experimental results have shown the effectiveness of our method in various domains, such as 2D images, videos, and 3D signed distance functions. Finally, we demonstrate that our proposed method improves training stability, by exploiting parameter sharing.