PIG: Physics-Informed Gaussians as Adaptive Parametric Mesh Representations

The approximation of Partial Differential Equations (PDEs) using neural networks has seen significant advancements through Physics-Informed Neural Networks (PINNs). Despite their straightforward optimization framework and flexibility in implementing various PDEs, PINNs often suffer from limited accuracy due to the spectral bias of Multi-Layer Perceptrons (MLPs), which struggle to effectively learn high-frequency and non-linear components. Recently, parametric mesh representations in combination with neural networks have been investigated as a promising approach to eliminate the inductive biases of neural networks. However, they usually require very high-resolution grids and a large number of collocation points to achieve high accuracy while avoiding overfitting issues. In addition, the fixed positions of the mesh parameters restrict their flexibility, making it challenging to accurately approximate complex PDEs. To overcome these limitations, we propose Physics-Informed Gaussians (PIGs), which combine feature embeddings using Gaussian functions with a lightweight neural network. Our approach uses trainable parameters for the mean and variance of each Gaussian, allowing for dynamic adjustment of their positions and shapes during training. This adaptability enables our model to optimally approximate PDE solutions, unlike models with fixed parameter positions. Furthermore, the proposed approach maintains the same optimization framework used in PINNs, allowing us to benefit from their excellent properties. Experimental results show the competitive performance of our model across various PDEs, demonstrating its potential as a robust tool for solving complex PDEs. Our project page is available at https://namgyukang.github.io/Physics-Informed-Gaussians/

PIXEL: Physics-Informed Cell Representations for Fast and Accurate PDE Solvers

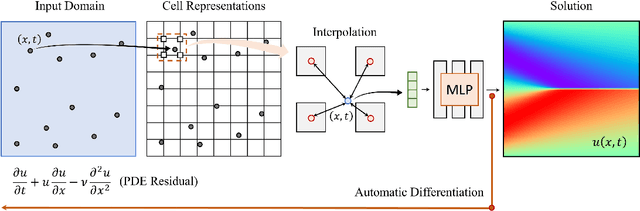
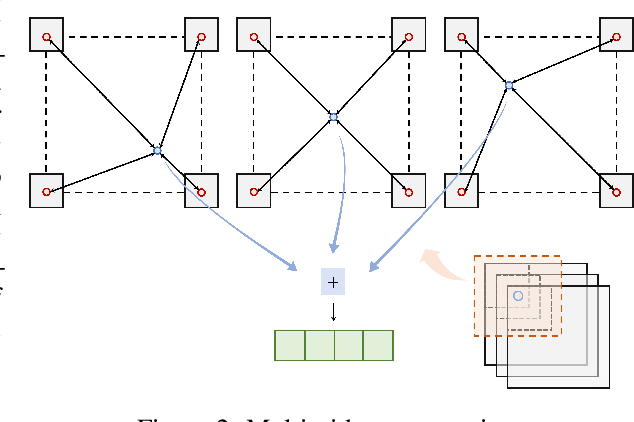
With the increases in computational power and advances in machine learning, data-driven learning-based methods have gained significant attention in solving PDEs. Physics-informed neural networks (PINNs) have recently emerged and succeeded in various forward and inverse PDEs problems thanks to their excellent properties, such as flexibility, mesh-free solutions, and unsupervised training. However, their slower convergence speed and relatively inaccurate solutions often limit their broader applicability in many science and engineering domains. This paper proposes a new kind of data-driven PDEs solver, physics-informed cell representations (PIXEL), elegantly combining classical numerical methods and learning-based approaches. We adopt a grid structure from the numerical methods to improve accuracy and convergence speed and overcome the spectral bias presented in PINNs. Moreover, the proposed method enjoys the same benefits in PINNs, e.g., using the same optimization frameworks to solve both forward and inverse PDE problems and readily enforcing PDE constraints with modern automatic differentiation techniques. We provide experimental results on various challenging PDEs that the original PINNs have struggled with and show that PIXEL achieves fast convergence speed and high accuracy.