Example-Based Concept Analysis Framework for Deep Weather Forecast Models

To improve the trustworthiness of an AI model, finding consistent, understandable representations of its inference process is essential. This understanding is particularly important in high-stakes operations such as weather forecasting, where the identification of underlying meteorological mechanisms is as critical as the accuracy of the predictions. Despite the growing literature that addresses this issue through explainable AI, the applicability of their solutions is often limited due to their AI-centric development. To fill this gap, we follow a user-centric process to develop an example-based concept analysis framework, which identifies cases that follow a similar inference process as the target instance in a target model and presents them in a user-comprehensible format. Our framework provides the users with visually and conceptually analogous examples, including the probability of concept assignment to resolve ambiguities in weather mechanisms. To bridge the gap between vector representations identified from models and human-understandable explanations, we compile a human-annotated concept dataset and implement a user interface to assist domain experts involved in the the framework development.

Explainable AI-Based Interface System for Weather Forecasting Model

Machine learning (ML) is becoming increasingly popular in meteorological decision-making. Although the literature on explainable artificial intelligence (XAI) is growing steadily, user-centered XAI studies have not extend to this domain yet. This study defines three requirements for explanations of black-box models in meteorology through user studies: statistical model performance for different rainfall scenarios to identify model bias, model reasoning, and the confidence of model outputs. Appropriate XAI methods are mapped to each requirement, and the generated explanations are tested quantitatively and qualitatively. An XAI interface system is designed based on user feedback. The results indicate that the explanations increase decision utility and user trust. Users prefer intuitive explanations over those based on XAI algorithms even for potentially easy-to-recognize examples. These findings can provide evidence for future research on user-centered XAI algorithms, as well as a basis to improve the usability of AI systems in practice.

Spectral operator learning for parametric PDEs without data reliance

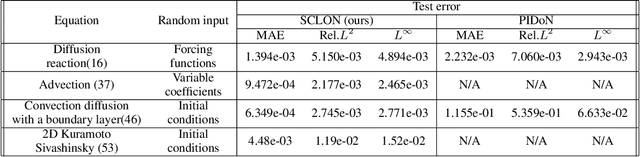
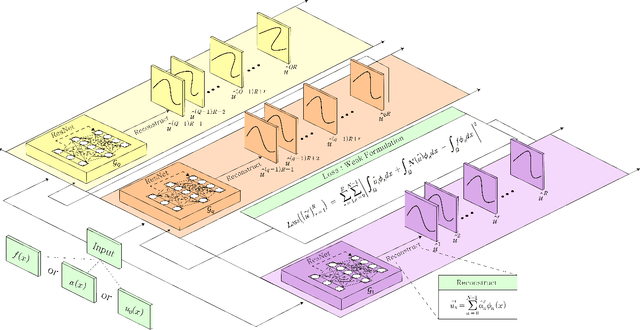
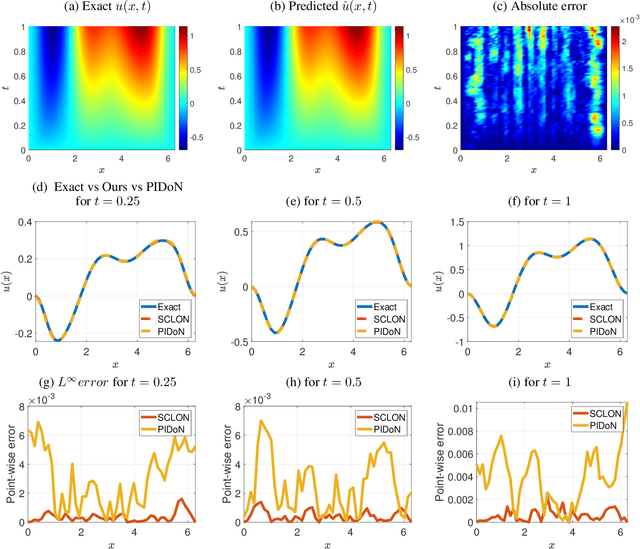
In this paper, we introduce the Spectral Coefficient Learning via Operator Network (SCLON), a novel operator learning-based approach for solving parametric partial differential equations (PDEs) without the need for data harnessing. The cornerstone of our method is the spectral methodology that employs expansions using orthogonal functions, such as Fourier series and Legendre polynomials, enabling accurate PDE solutions with fewer grid points. By merging the merits of spectral methods - encompassing high accuracy, efficiency, generalization, and the exact fulfillment of boundary conditions - with the prowess of deep neural networks, SCLON offers a transformative strategy. Our approach not only eliminates the need for paired input-output training data, which typically requires extensive numerical computations, but also effectively learns and predicts solutions of complex parametric PDEs, ranging from singularly perturbed convection-diffusion equations to the Navier-Stokes equations. The proposed framework demonstrates superior performance compared to existing scientific machine learning techniques, offering solutions for multiple instances of parametric PDEs without harnessing data. The mathematical framework is robust and reliable, with a well-developed loss function derived from the weak formulation, ensuring accurate approximation of solutions while exactly satisfying boundary conditions. The method's efficacy is further illustrated through its ability to accurately predict intricate natural behaviors like the Kolmogorov flow and boundary layers. In essence, our work pioneers a compelling avenue for parametric PDE solutions, serving as a bridge between traditional numerical methodologies and cutting-edge machine learning techniques in the realm of scientific computation.

Unsupervised Legendre-Galerkin Neural Network for Stiff Partial Differential Equations

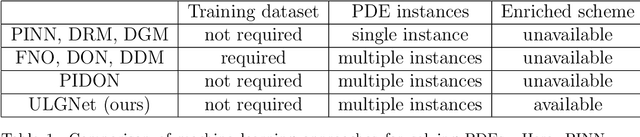
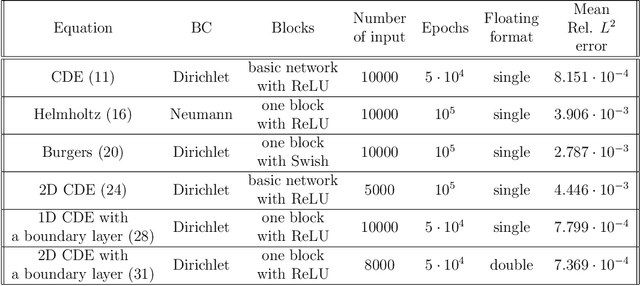
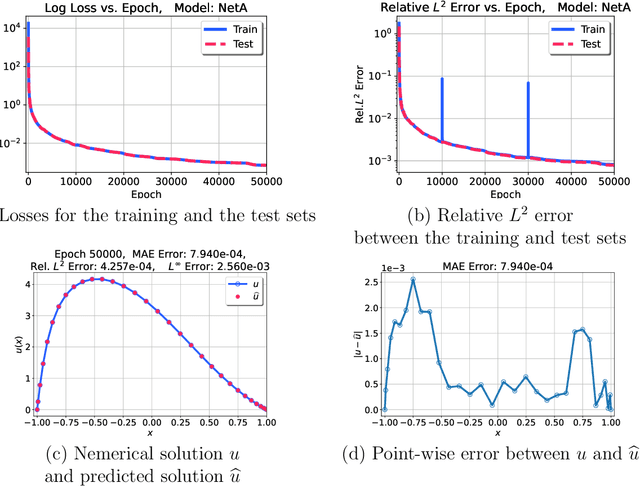
Machine learning methods have been lately used to solve differential equations and dynamical systems. These approaches have been developed into a novel research field known as scientific machine learning in which techniques such as deep neural networks and statistical learning are applied to classical problems of applied mathematics. Because neural networks provide an approximation capability, computational parameterization through machine learning and optimization methods achieve noticeable performance when solving various partial differential equations (PDEs). In this paper, we develop a novel numerical algorithm that incorporates machine learning and artificial intelligence to solve PDEs. In particular, we propose an unsupervised machine learning algorithm based on the Legendre-Galerkin neural network to find an accurate approximation to the solution of different types of PDEs. The proposed neural network is applied to the general 1D and 2D PDEs as well as singularly perturbed PDEs that possess boundary layer behavior.

MIR-VIO: Mutual Information Residual-based Visual Inertial Odometry with UWB Fusion for Robust Localization

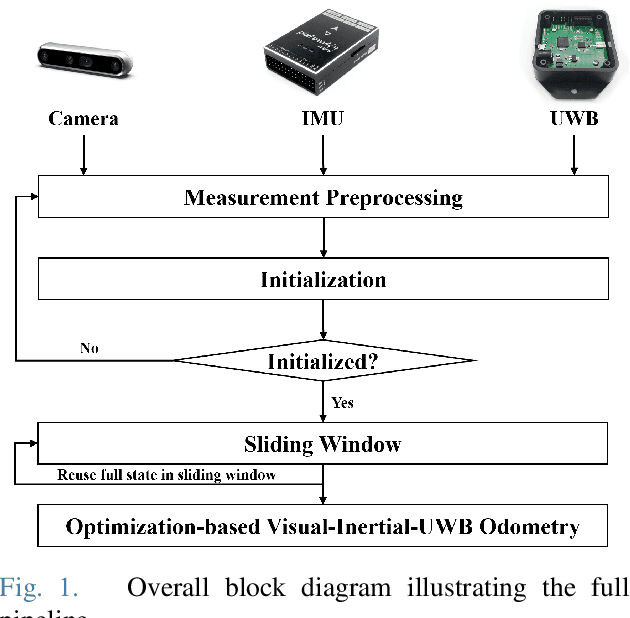
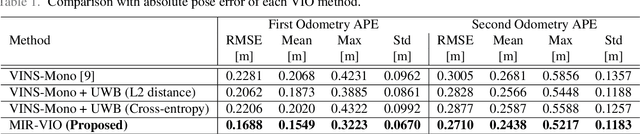
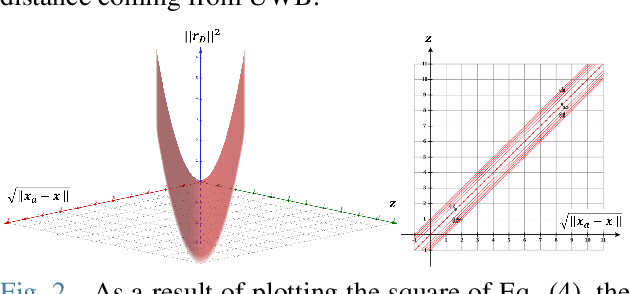
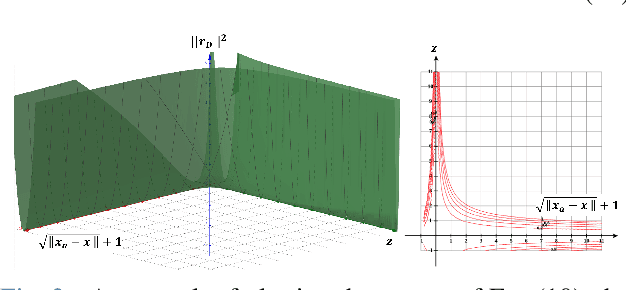
For many years, there has been an impressive progress on visual odometry applied to mobile robots and drones. However, the visual perception is still in the spotlight as a challenging field because the vision sensor has some problems in obtaining correct scale information with a monocular camera and also is vulnerable to a situation in which illumination is changed. In this paper, UWB sensor fusion is proposed in the visual inertial odometry algorithm as a solution to mitigate this problem. We designed a cost function based on mutual information considering the UWB. Considering the characteristic of the UWB signal model, where the uncertainty increases as the distance between the UWB anchor and the tag increases, we introduced a new residual term to the cost function. When the experiment was conducted in an indoor environment with the above methodology, the initialization problem in an environment with few feature points was solved through the UWB sensor fusion, and localization became robust. And when the residual term using the concept of mutual information was used, the most robust odometry could be obtained.

REAL: Rapid Exploration with Active Loop-Closing toward Large-Scale 3D Mapping using UAVs

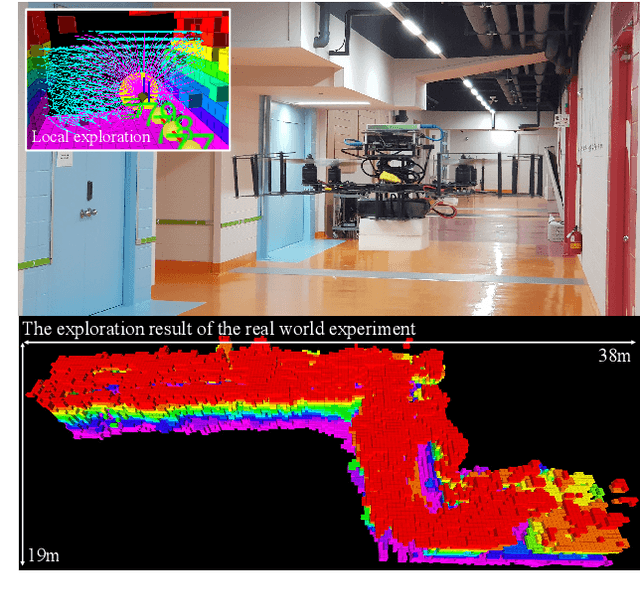
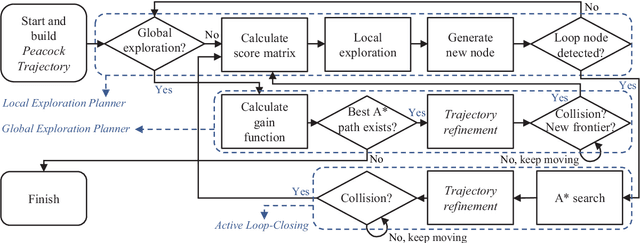
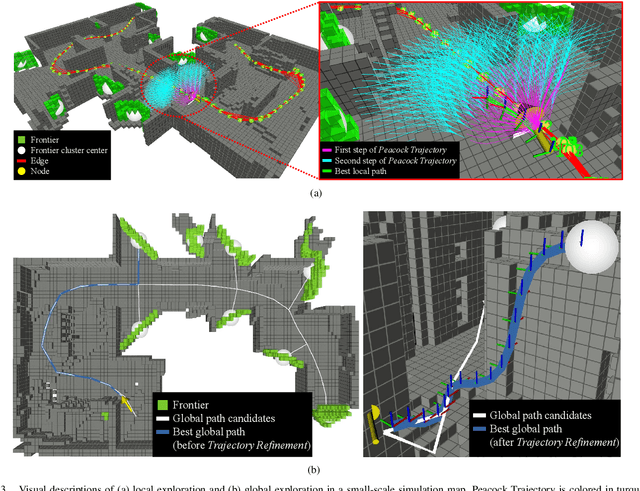
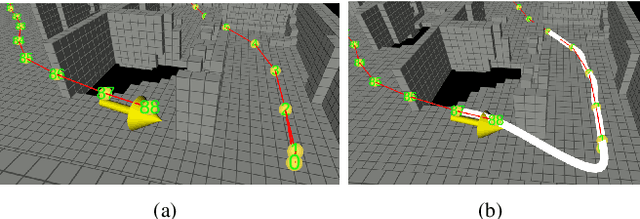
Exploring an unknown environment without colliding with obstacles is one of the essentials of autonomous vehicles to perform diverse missions such as structural inspections, rescues, deliveries, and so forth. Therefore, unmanned aerial vehicles (UAVs), which are fast, agile, and have high degrees of freedom, have been widely used. However, previous approaches have two limitations: a) First, they may not be appropriate for exploring large-scale environments because they mainly depend on random sampling-based path planning that causes unnecessary movements. b) Second, they assume the pose estimation is accurate enough, which is the most critical factor in obtaining an accurate map. In this paper, to explore and map unknown large-scale environments rapidly and accurately, we propose a novel exploration method that combines the pre-calculated Peacock Trajectory with graph-based global exploration and active loop-closing. Because the two-step trajectory that considers the kinodynamics of UAVs is used, obstacle avoidance is guaranteed in the receding-horizon manner. In addition, local exploration that considers the frontier and global exploration based on the graph maximizes the speed of exploration by minimizing unnecessary revisiting. In addition, by actively closing the loop based on the likelihood, pose estimation performance is improved. The proposed method's performance is verified by exploring 3D simulation environments in comparison with the state-of-the-art methods. Finally, the proposed approach is validated in a real-world experiment.

BRM Localization: UAV Localization in GNSS-Denied Environments Based on Matching of Numerical Map and UAV Images

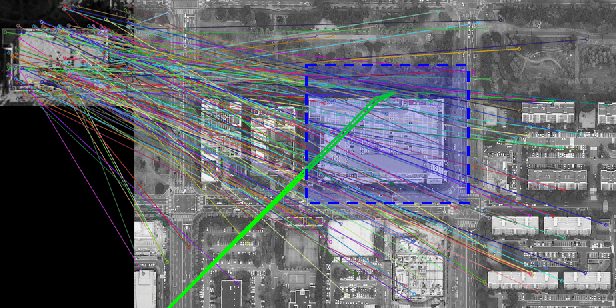
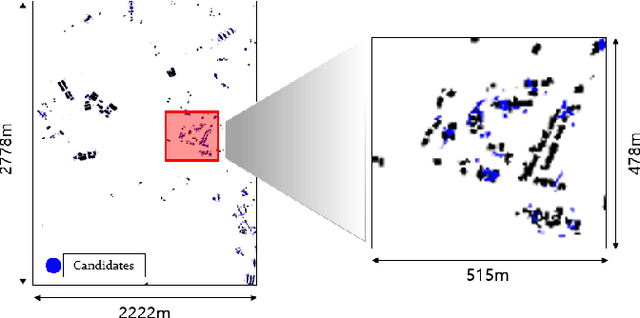
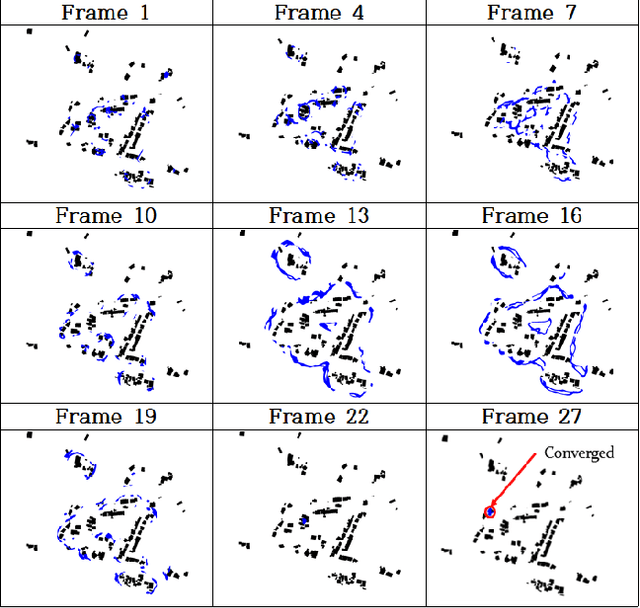
Localization is one of the most important technologies needed to use Unmanned Aerial Vehicles (UAVs) in actual fields. Currently, most UAVs use GNSS to estimate their position. Recently, there have been attacks that target the weaknesses of UAVs that use GNSS, such as interrupting GNSS signal to crash the UAVs or sending fake GNSS signals to hijack the UAVs. To avoid this kind of situation, this paper proposes an algorithm that deals with the localization problem of the UAV in GNSS-denied environments. We propose a localization method, named as BRM (Building Ratio Map based) localization, for a UAV by matching an existing numerical map with UAV images. The building area is extracted from the UAV images. The ratio of buildings that occupy in the corresponding image frame is calculated and matched with the building information on the numerical map. The position estimation is started in the range of several km^2 area, so that the position estimation can be performed without knowing the exact initial coordinate. Only freely available maps are used for training data set and matching the ground truth. Finally, we get real UAV images, IMU data, and GNSS data from UAV flight to show that the proposed method can achieve better performance than the conventional methods.