Anthony Gruber
Interpreting Transformer Architectures as Implicit Multinomial Regression
Sep 04, 2025Abstract:Mechanistic interpretability aims to understand how internal components of modern machine learning models, such as weights, activations, and layers, give rise to the model's overall behavior. One particularly opaque mechanism is attention: despite its central role in transformer models, its mathematical underpinnings and relationship to concepts like feature polysemanticity, superposition, and model performance remain poorly understood. This paper establishes a novel connection between attention mechanisms and multinomial regression. Specifically, we show that in a fixed multinomial regression setting, optimizing over latent features yields optimal solutions that align with the dynamics induced by attention blocks. In other words, the evolution of representations through a transformer can be interpreted as a trajectory that recovers the optimal features for classification.
Thermodynamically Consistent Latent Dynamics Identification for Parametric Systems
Jun 10, 2025Abstract:We propose an efficient thermodynamics-informed latent space dynamics identification (tLaSDI) framework for the reduced-order modeling of parametric nonlinear dynamical systems. This framework integrates autoencoders for dimensionality reduction with newly developed parametric GENERIC formalism-informed neural networks (pGFINNs), which enable efficient learning of parametric latent dynamics while preserving key thermodynamic principles such as free energy conservation and entropy generation across the parameter space. To further enhance model performance, a physics-informed active learning strategy is incorporated, leveraging a greedy, residual-based error indicator to adaptively sample informative training data, outperforming uniform sampling at equivalent computational cost. Numerical experiments on the Burgers' equation and the 1D/1V Vlasov-Poisson equation demonstrate that the proposed method achieves up to 3,528x speed-up with 1-3% relative errors, and significant reduction in training (50-90%) and inference (57-61%) cost. Moreover, the learned latent space dynamics reveal the underlying thermodynamic behavior of the system, offering valuable insights into the physical-space dynamics.
Understanding and Mitigating Membership Inference Risks of Neural Ordinary Differential Equations
Jan 12, 2025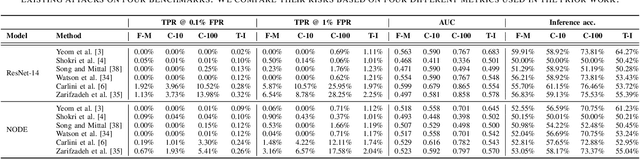

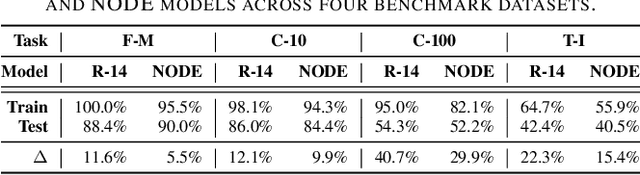

Abstract:Neural ordinary differential equations (NODEs) are an emerging paradigm in scientific computing for modeling dynamical systems. By accurately learning underlying dynamics in data in the form of differential equations, NODEs have been widely adopted in various domains, such as healthcare, finance, computer vision, and language modeling. However, there remains a limited understanding of the privacy implications of these fundamentally different models, particularly with regard to their membership inference risks. In this work, we study the membership inference risks associated with NODEs. We first comprehensively evaluate NODEs against membership inference attacks. We show that NODEs are twice as resistant to these privacy attacks compared to conventional feedforward models such as ResNets. By analyzing the variance in membership risks across different NODE models, we identify the factors that contribute to their lower risks. We then demonstrate, both theoretically and empirically, that membership inference risks can be further mitigated by utilizing a stochastic variant of NODEs: Neural stochastic differential equations (NSDEs). We show that NSDEs are differentially-private (DP) learners that provide the same provable privacy guarantees as DP-SGD, the de-facto mechanism for training private models. NSDEs are also effective in mitigating existing membership inference attacks, demonstrating risks comparable to private models trained with DP-SGD while offering an improved privacy-utility trade-off. Moreover, we propose a drop-in-replacement strategy that efficiently integrates NSDEs into conventional feedforward models to enhance their privacy.
MaD-Scientist: AI-based Scientist solving Convection-Diffusion-Reaction Equations Using Massive PINN-Based Prior Data
Oct 09, 2024



Abstract:Large language models (LLMs), like ChatGPT, have shown that even trained with noisy prior data, they can generalize effectively to new tasks through in-context learning (ICL) and pre-training techniques. Motivated by this, we explore whether a similar approach can be applied to scientific foundation models (SFMs). Our methodology is structured as follows: (i) we collect low-cost physics-informed neural network (PINN)-based approximated prior data in the form of solutions to partial differential equations (PDEs) constructed through an arbitrary linear combination of mathematical dictionaries; (ii) we utilize Transformer architectures with self and cross-attention mechanisms to predict PDE solutions without knowledge of the governing equations in a zero-shot setting; (iii) we provide experimental evidence on the one-dimensional convection-diffusion-reaction equation, which demonstrate that pre-training remains robust even with approximated prior data, with only marginal impacts on test accuracy. Notably, this finding opens the path to pre-training SFMs with realistic, low-cost data instead of (or in conjunction with) numerical high-cost data. These results support the conjecture that SFMs can improve in a manner similar to LLMs, where fully cleaning the vast set of sentences crawled from the Internet is nearly impossible.
Gaussian Variational Schemes on Bounded and Unbounded Domains
Oct 08, 2024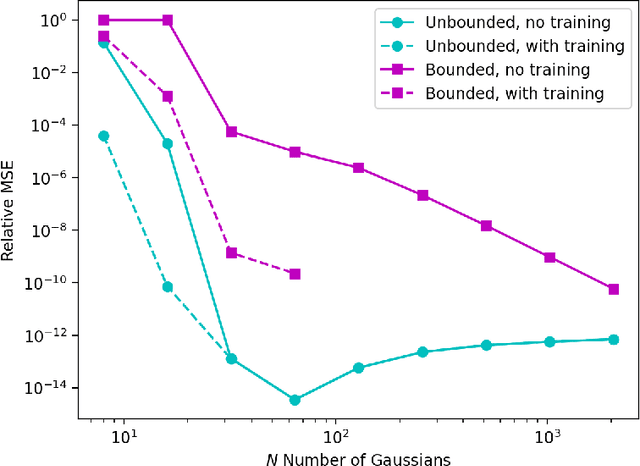
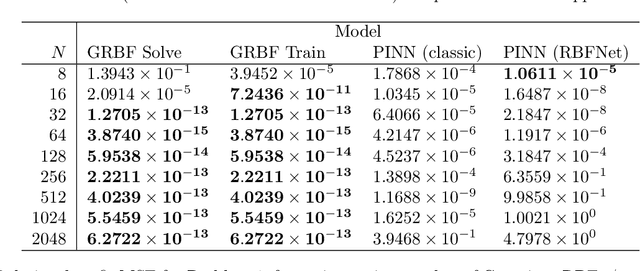

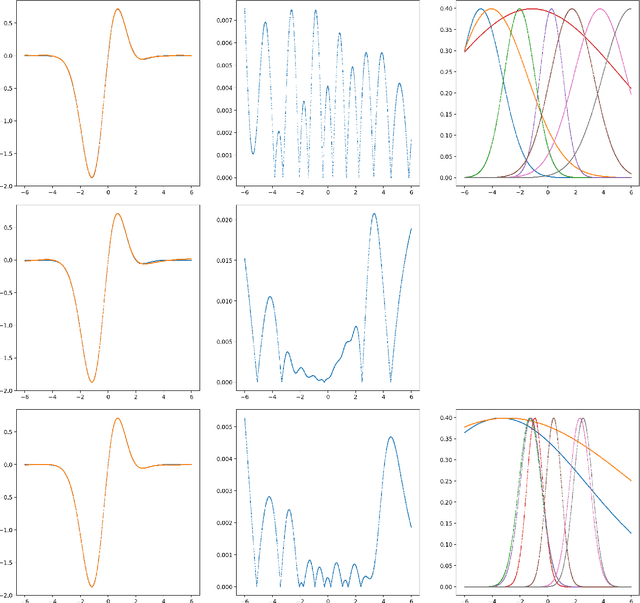
Abstract:A machine-learnable variational scheme using Gaussian radial basis functions (GRBFs) is presented and used to approximate linear problems on bounded and unbounded domains. In contrast to standard mesh-free methods, which use GRBFs to discretize strong-form differential equations, this work exploits the relationship between integrals of GRBFs, their derivatives, and polynomial moments to produce exact quadrature formulae which enable weak-form expressions. Combined with trainable GRBF means and covariances, this leads to a flexible, generalized Galerkin variational framework which is applied in the infinite-domain setting where the scheme is conforming, as well as the bounded-domain setting where it is not. Error rates for the proposed GRBF scheme are derived in each case, and examples are presented demonstrating utility of this approach as a surrogate modeling technique.
Efficiently Parameterized Neural Metriplectic Systems
May 28, 2024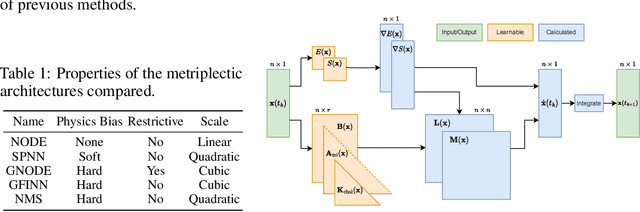

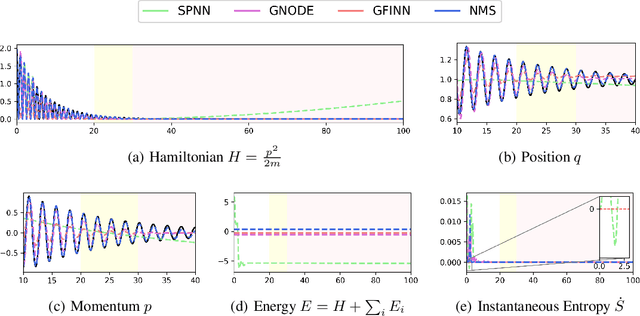
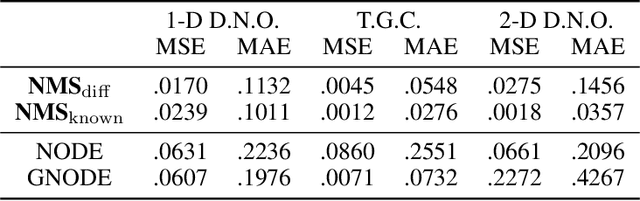
Abstract:Metriplectic systems are learned from data in a way that scales quadratically in both the size of the state and the rank of the metriplectic data. Besides being provably energy conserving and entropy stable, the proposed approach comes with approximation results demonstrating its ability to accurately learn metriplectic dynamics from data as well as an error estimate indicating its potential for generalization to unseen timescales when approximation error is low. Examples are provided which illustrate performance in the presence of both full state information as well as when entropic variables are unknown, confirming that the proposed approach exhibits superior accuracy and scalability without compromising on model expressivity.
Reversible and irreversible bracket-based dynamics for deep graph neural networks
May 24, 2023Abstract:Recent works have shown that physics-inspired architectures allow the training of deep graph neural networks (GNNs) without oversmoothing. The role of these physics is unclear, however, with successful examples of both reversible (e.g., Hamiltonian) and irreversible (e.g., diffusion) phenomena producing comparable results despite diametrically opposed mechanisms, and further complications arising due to empirical departures from mathematical theory. This work presents a series of novel GNN architectures based upon structure-preserving bracket-based dynamical systems, which are provably guaranteed to either conserve energy or generate positive dissipation with increasing depth. It is shown that the theoretically principled framework employed here allows for inherently explainable constructions, which contextualize departures from theory in current architectures and better elucidate the roles of reversibility and irreversibility in network performance.
Canonical and Noncanonical Hamiltonian Operator Inference
Apr 13, 2023
Abstract:A method for the nonintrusive and structure-preserving model reduction of canonical and noncanonical Hamiltonian systems is presented. Based on the idea of operator inference, this technique is provably convergent and reduces to a straightforward linear solve given snapshot data and gray-box knowledge of the system Hamiltonian. Examples involving several hyperbolic partial differential equations show that the proposed method yields reduced models which, in addition to being accurate and stable with respect to the addition of basis modes, preserve conserved quantities well outside the range of their training data.
Level set learning with pseudo-reversible neural networks for nonlinear dimension reduction in function approximation
Dec 02, 2021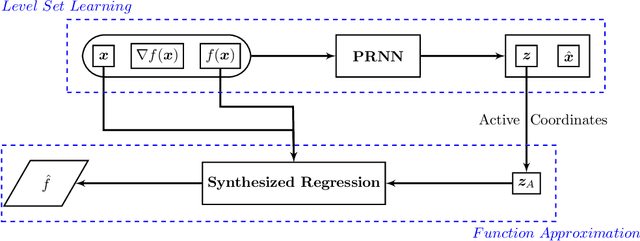

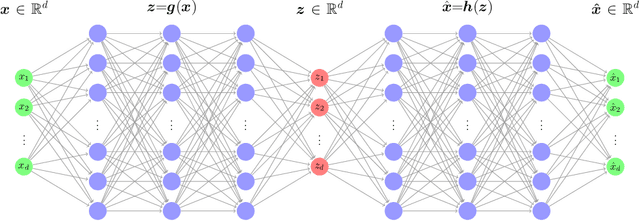
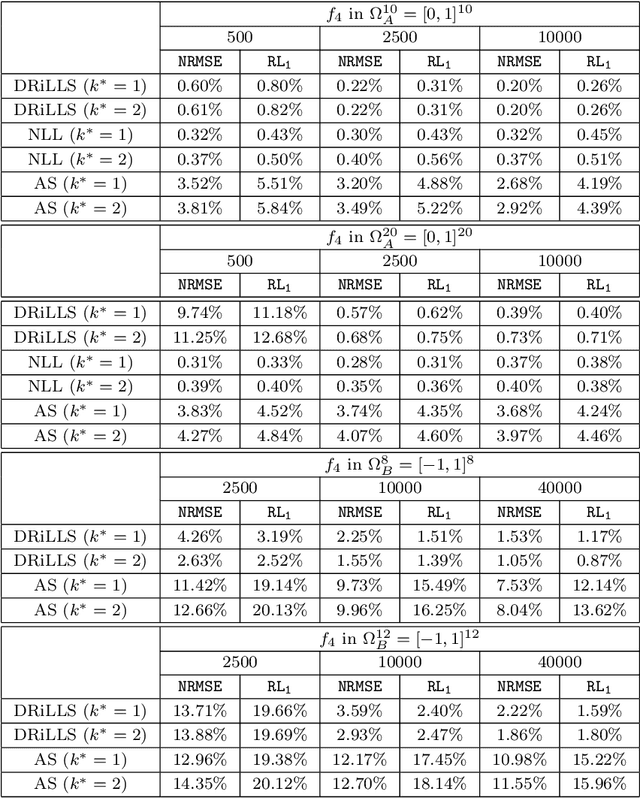
Abstract:Due to the curse of dimensionality and the limitation on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method of Dimension Reduction via Learning Level Sets (DRiLLS) for function approximation. Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. The PRNN not only relaxes the invertibility constraint of the nonlinear transformation present in the NLL method due to the use of RevNet, but also adaptively weights the influence of each sample and controls the sensitivity of the function to the learned active variables. The synthesized regression uses Euclidean distance in the input space to select neighboring samples, whose projections on the space of active variables are used to perform local least-squares polynomial fitting. This helps to resolve numerical oscillation issues present in traditional local and global regressions. Extensive experimental results demonstrate that our DRiLLS method outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.
A Comparison of Neural Network Architectures for Data-Driven Reduced-Order Modeling
Oct 05, 2021
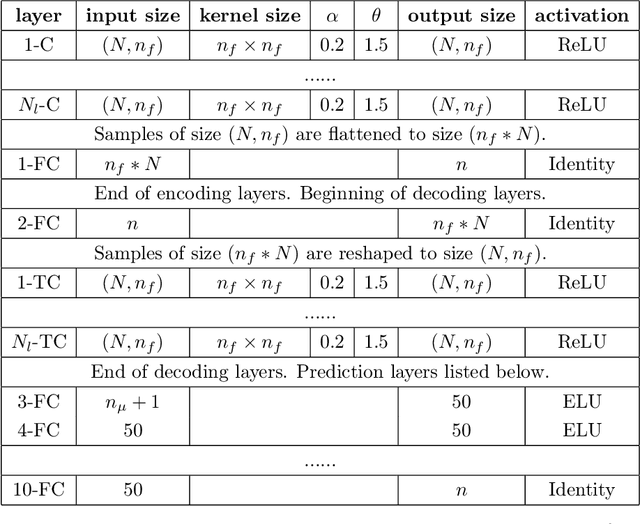

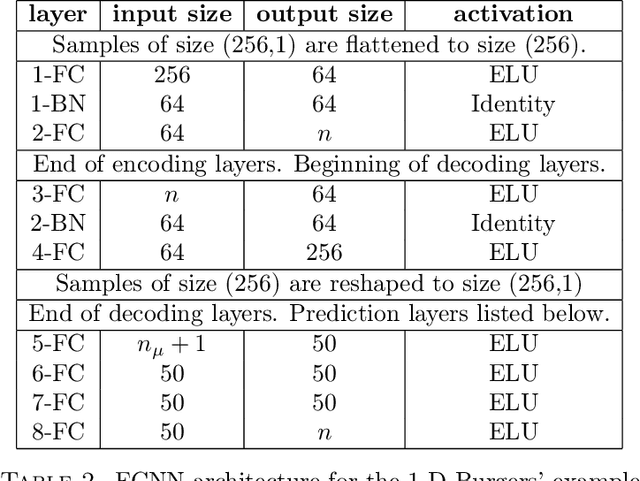
Abstract:The popularity of deep convolutional autoencoders (CAEs) has engendered effective reduced-order models (ROMs) for the simulation of large-scale dynamical systems. However, it is not known whether deep CAEs provide superior performance in all ROM scenarios. To elucidate this, the effect of autoencoder architecture on its associated ROM is studied through the comparison of deep CAEs against two alternatives: a simple fully connected autoencoder, and a novel graph convolutional autoencoder. Through benchmark experiments, it is shown that the superior autoencoder architecture for a given ROM application is highly dependent on the size of the latent space and the structure of the snapshot data, with the proposed architecture demonstrating benefits on data with irregular connectivity when the latent space is sufficiently large.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge