Gaussian Variational Schemes on Bounded and Unbounded Domains
Paper and Code
Oct 08, 2024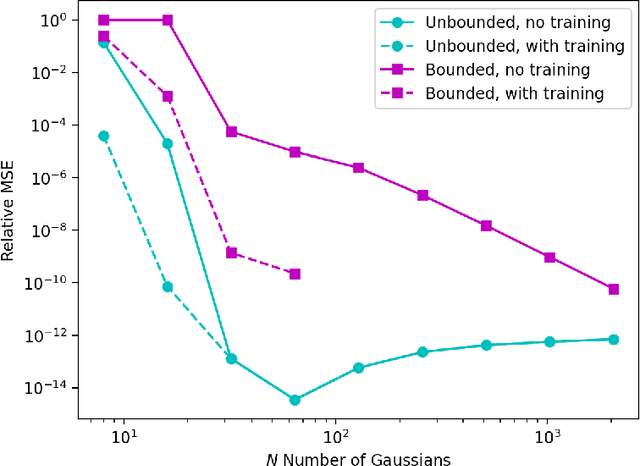
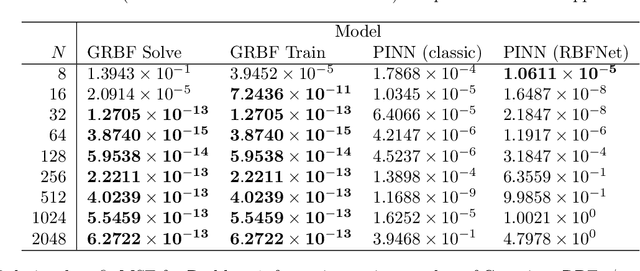

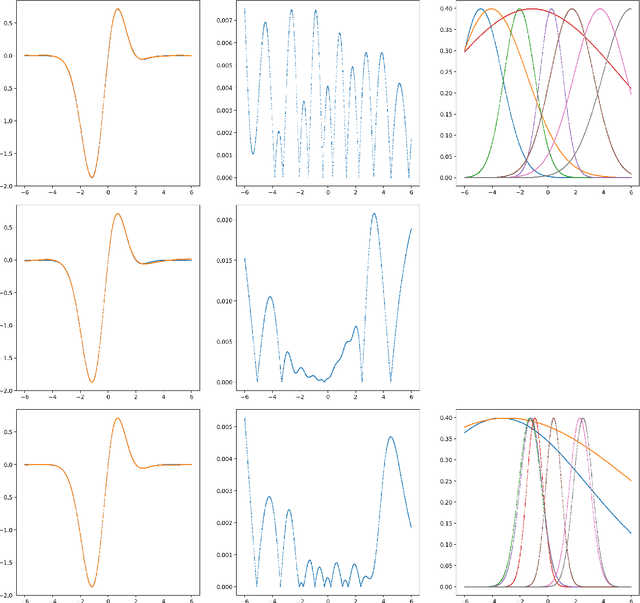
A machine-learnable variational scheme using Gaussian radial basis functions (GRBFs) is presented and used to approximate linear problems on bounded and unbounded domains. In contrast to standard mesh-free methods, which use GRBFs to discretize strong-form differential equations, this work exploits the relationship between integrals of GRBFs, their derivatives, and polynomial moments to produce exact quadrature formulae which enable weak-form expressions. Combined with trainable GRBF means and covariances, this leads to a flexible, generalized Galerkin variational framework which is applied in the infinite-domain setting where the scheme is conforming, as well as the bounded-domain setting where it is not. Error rates for the proposed GRBF scheme are derived in each case, and examples are presented demonstrating utility of this approach as a surrogate modeling technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge