An End-to-End Deep Learning Method for Solving Nonlocal Allen-Cahn and Cahn-Hilliard Phase-Field Models

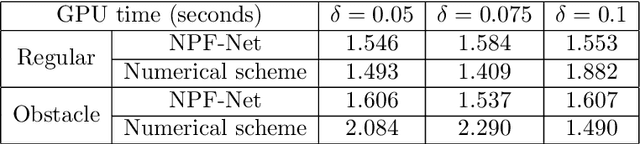
We propose an efficient end-to-end deep learning method for solving nonlocal Allen-Cahn (AC) and Cahn-Hilliard (CH) phase-field models. One motivation for this effort emanates from the fact that discretized partial differential equation-based AC or CH phase-field models result in diffuse interfaces between phases, with the only recourse for remediation is to severely refine the spatial grids in the vicinity of the true moving sharp interface whose width is determined by a grid-independent parameter that is substantially larger than the local grid size. In this work, we introduce non-mass conserving nonlocal AC or CH phase-field models with regular, logarithmic, or obstacle double-well potentials. Because of non-locality, some of these models feature totally sharp interfaces separating phases. The discretization of such models can lead to a transition between phases whose width is only a single grid cell wide. Another motivation is to use deep learning approaches to ameliorate the otherwise high cost of solving discretized nonlocal phase-field models. To this end, loss functions of the customized neural networks are defined using the residual of the fully discrete approximations of the AC or CH models, which results from applying a Fourier collocation method and a temporal semi-implicit approximation. To address the long-range interactions in the models, we tailor the architecture of the neural network by incorporating a nonlocal kernel as an input channel to the neural network model. We then provide the results of extensive computational experiments to illustrate the accuracy, structure-preserving properties, predictive capabilities, and cost reductions of the proposed method.

A Comparison of Neural Network Architectures for Data-Driven Reduced-Order Modeling

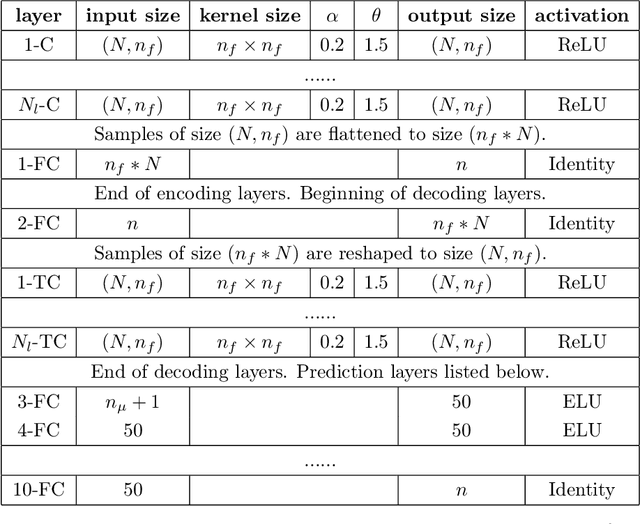
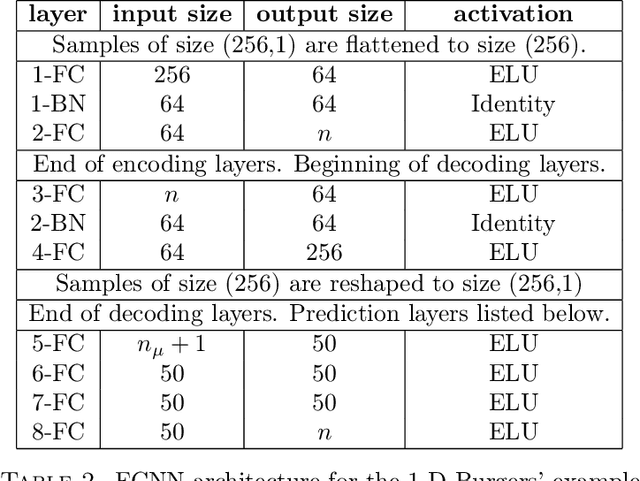
The popularity of deep convolutional autoencoders (CAEs) has engendered effective reduced-order models (ROMs) for the simulation of large-scale dynamical systems. However, it is not known whether deep CAEs provide superior performance in all ROM scenarios. To elucidate this, the effect of autoencoder architecture on its associated ROM is studied through the comparison of deep CAEs against two alternatives: a simple fully connected autoencoder, and a novel graph convolutional autoencoder. Through benchmark experiments, it is shown that the superior autoencoder architecture for a given ROM application is highly dependent on the size of the latent space and the structure of the snapshot data, with the proposed architecture demonstrating benefits on data with irregular connectivity when the latent space is sufficiently large.

Nonlinear Level Set Learning for Function Approximation on Sparse Data with Applications to Parametric Differential Equations

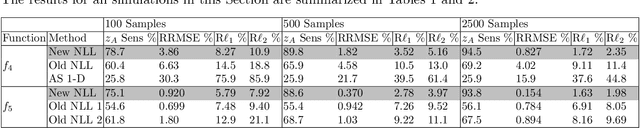
A dimension reduction method based on the "Nonlinear Level set Learning" (NLL) approach is presented for the pointwise prediction of functions which have been sparsely sampled. Leveraging geometric information provided by the Implicit Function Theorem, the proposed algorithm effectively reduces the input dimension to the theoretical lower bound with minor accuracy loss, providing a one-dimensional representation of the function which can be used for regression and sensitivity analysis. Experiments and applications are presented which compare this modified NLL with the original NLL and the Active Subspaces (AS) method. While accommodating sparse input data, the proposed algorithm is shown to train quickly and provide a much more accurate and informative reduction than either AS or the original NLL on two example functions with high-dimensional domains, as well as two state-dependent quantities depending on the solutions to parametric differential equations.