Level set learning with pseudo-reversible neural networks for nonlinear dimension reduction in function approximation

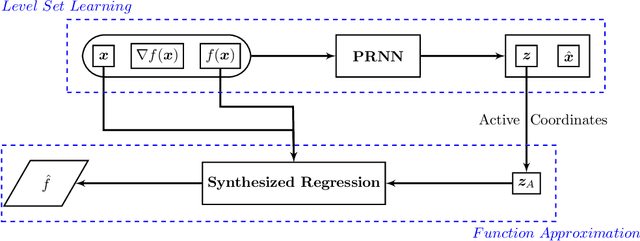
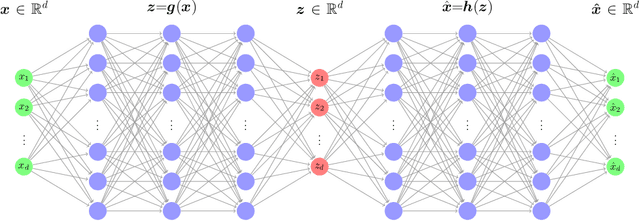
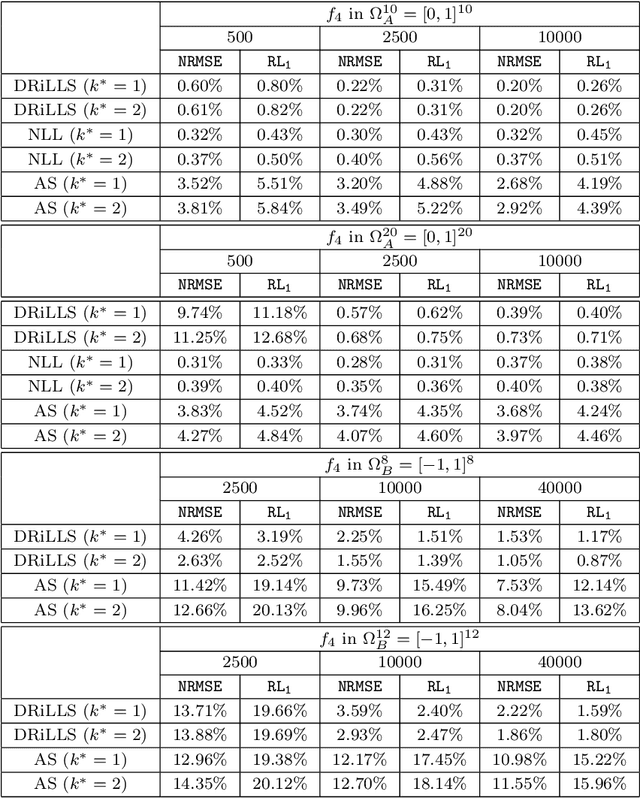
Due to the curse of dimensionality and the limitation on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method of Dimension Reduction via Learning Level Sets (DRiLLS) for function approximation. Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. The PRNN not only relaxes the invertibility constraint of the nonlinear transformation present in the NLL method due to the use of RevNet, but also adaptively weights the influence of each sample and controls the sensitivity of the function to the learned active variables. The synthesized regression uses Euclidean distance in the input space to select neighboring samples, whose projections on the space of active variables are used to perform local least-squares polynomial fitting. This helps to resolve numerical oscillation issues present in traditional local and global regressions. Extensive experimental results demonstrate that our DRiLLS method outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.

Learning Green's Functions of Linear Reaction-Diffusion Equations with Application to Fast Numerical Solver

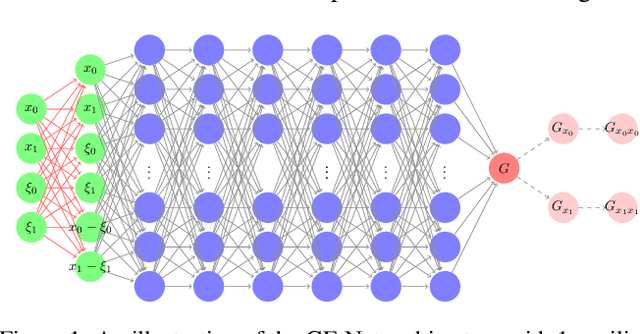
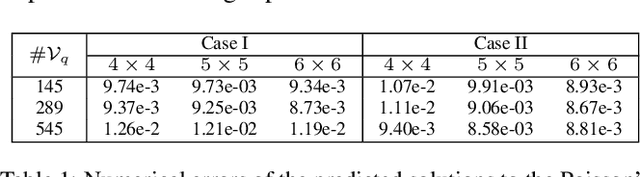
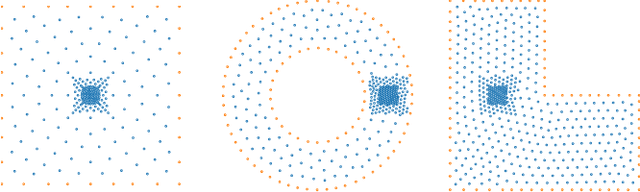
Partial differential equations are often used to model various physical phenomena, such as heat diffusion, wave propagation, fluid dynamics, elasticity, electrodynamics and image processing, and many analytic approaches or traditional numerical methods have been developed and widely used for their solutions. Inspired by rapidly growing impact of deep learning on scientific and engineering research, in this paper we propose a novel neural network, GF-Net, for learning the Green's functions of linear reaction-diffusion equations in an unsupervised fashion. The proposed method overcomes the challenges for finding the Green's functions of the equations on arbitrary domains by utilizing physics-informed approach and the symmetry of the Green's function. As a consequence, it particularly leads to an efficient way for solving the target equations under different boundary conditions and sources. We also demonstrate the effectiveness of the proposed approach by experiments in square, annular and L-shape domains.

Nonlinear Level Set Learning for Function Approximation on Sparse Data with Applications to Parametric Differential Equations

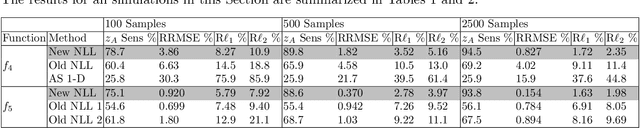
A dimension reduction method based on the "Nonlinear Level set Learning" (NLL) approach is presented for the pointwise prediction of functions which have been sparsely sampled. Leveraging geometric information provided by the Implicit Function Theorem, the proposed algorithm effectively reduces the input dimension to the theoretical lower bound with minor accuracy loss, providing a one-dimensional representation of the function which can be used for regression and sensitivity analysis. Experiments and applications are presented which compare this modified NLL with the original NLL and the Active Subspaces (AS) method. While accommodating sparse input data, the proposed algorithm is shown to train quickly and provide a much more accurate and informative reduction than either AS or the original NLL on two example functions with high-dimensional domains, as well as two state-dependent quantities depending on the solutions to parametric differential equations.

Interactive Binary Image Segmentation with Edge Preservation

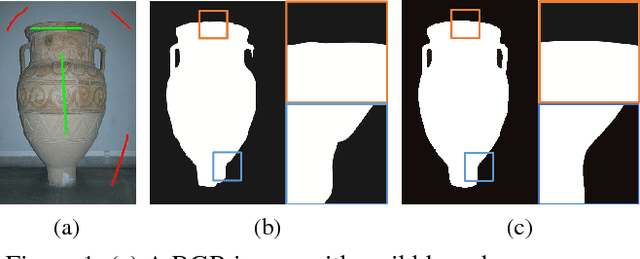
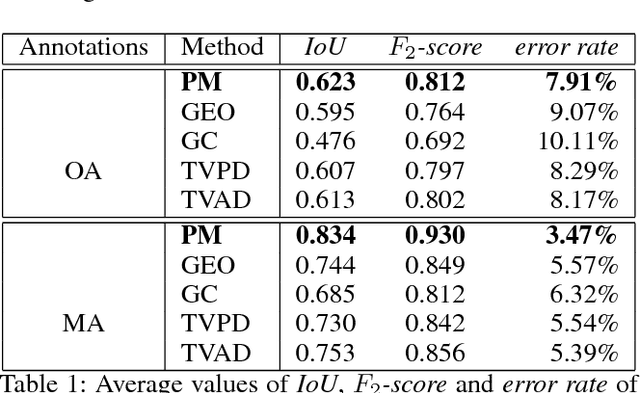
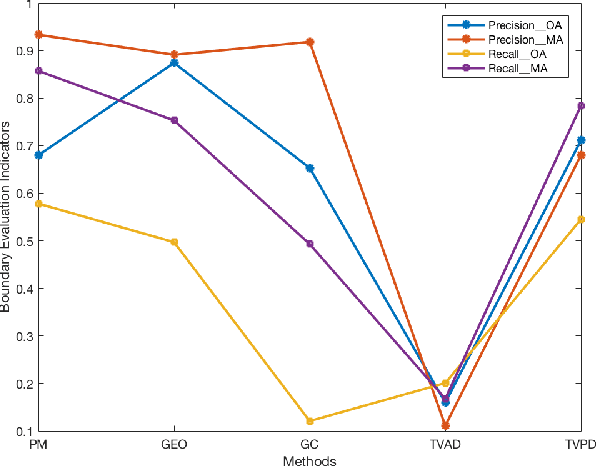
Binary image segmentation plays an important role in computer vision and has been widely used in many applications such as image and video editing, object extraction, and photo composition. In this paper, we propose a novel interactive binary image segmentation method based on the Markov Random Field (MRF) framework and the fast bilateral solver (FBS) technique. Specifically, we employ the geodesic distance component to build the unary term. To ensure both computation efficiency and effective responsiveness for interactive segmentation, superpixels are used in computing geodesic distances instead of pixels. Furthermore, we take a bilateral affinity approach for the pairwise term in order to preserve edge information and denoise. Through the alternating direction strategy, the MRF energy minimization problem is divided into two subproblems, which then can be easily solved by steepest gradient descent (SGD) and FBS respectively. Experimental results on the VGG interactive image segmentation dataset show that the proposed algorithm outperforms several state-of-the-art ones, and in particular, it can achieve satisfactory edge-smooth segmentation results even when the foreground and background color appearances are quite indistinctive.