A Score-based Diffusion Model Approach for Adaptive Learning of Stochastic Partial Differential Equation Solutions

We propose a novel framework for adaptively learning the time-evolving solutions of stochastic partial differential equations (SPDEs) using score-based diffusion models within a recursive Bayesian inference setting. SPDEs play a central role in modeling complex physical systems under uncertainty, but their numerical solutions often suffer from model errors and reduced accuracy due to incomplete physical knowledge and environmental variability. To address these challenges, we encode the governing physics into the score function of a diffusion model using simulation data and incorporate observational information via a likelihood-based correction in a reverse-time stochastic differential equation. This enables adaptive learning through iterative refinement of the solution as new data becomes available. To improve computational efficiency in high-dimensional settings, we introduce the ensemble score filter, a training-free approximation of the score function designed for real-time inference. Numerical experiments on benchmark SPDEs demonstrate the accuracy and robustness of the proposed method under sparse and noisy observations.

Frequency-Aware Density Control via Reparameterization for High-Quality Rendering of 3D Gaussian Splatting

By adaptively controlling the density and generating more Gaussians in regions with high-frequency information, 3D Gaussian Splatting (3DGS) can better represent scene details. From the signal processing perspective, representing details usually needs more Gaussians with relatively smaller scales. However, 3DGS currently lacks an explicit constraint linking the density and scale of 3D Gaussians across the domain, leading to 3DGS using improper-scale Gaussians to express frequency information, resulting in the loss of accuracy. In this paper, we propose to establish a direct relation between density and scale through the reparameterization of the scaling parameters and ensure the consistency between them via explicit constraints (i.e., density responds well to changes in frequency). Furthermore, we develop a frequency-aware density control strategy, consisting of densification and deletion, to improve representation quality with fewer Gaussians. A dynamic threshold encourages densification in high-frequency regions, while a scale-based filter deletes Gaussians with improper scale. Experimental results on various datasets demonstrate that our method outperforms existing state-of-the-art methods quantitatively and qualitatively.

A Multiple Transferable Neural Network Method with Domain Decomposition for Elliptic Interface Problems

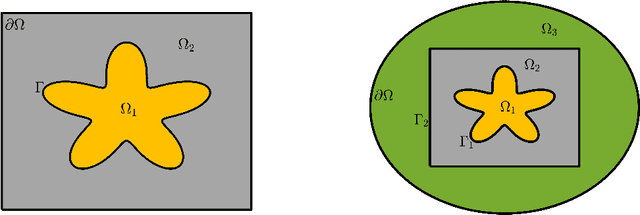
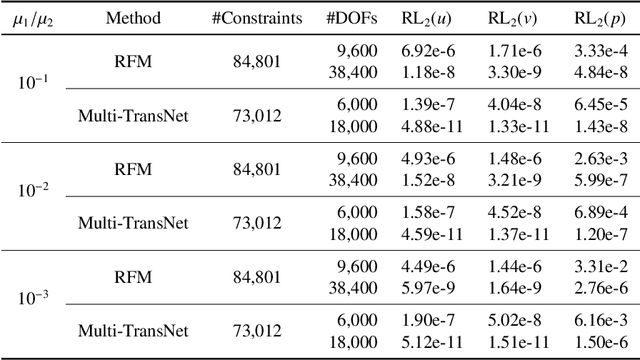
The transferable neural network (TransNet) is a two-layer shallow neural network with pre-determined and uniformly distributed neurons in the hidden layer, and the least-squares solvers can be particularly used to compute the parameters of its output layer when applied to the solution of partial differential equations. In this paper, we integrate the TransNet technique with the nonoverlapping domain decomposition and the interface conditions to develop a novel multiple transferable neural network (Multi-TransNet) method for solving elliptic interface problems, which typically contain discontinuities in both solutions and their derivatives across interfaces. We first propose an empirical formula for the TransNet to characterize the relationship between the radius of the domain-covering ball, the number of hidden-layer neurons, and the optimal neuron shape. In the Multi-TransNet method, we assign each subdomain one distinct TransNet with an adaptively determined number of hidden-layer neurons to maintain the globally uniform neuron distribution across the entire computational domain, and then unite all the subdomain TransNets together by incorporating the interface condition terms into the loss function. The empirical formula is also extended to the Multi-TransNet and further employed to estimate appropriate neuron shapes for the subdomain TransNets, greatly reducing the parameter tuning cost. Additionally, we propose a normalization approach to adaptively select the weighting parameters for the terms in the loss function. Ablation studies and extensive experiments with comparison tests on different types of elliptic interface problems with low to high contrast diffusion coefficients in two and three dimensions are carried out to numerically demonstrate the superior accuracy, efficiency, and robustness of the proposed Multi-TransNet method.

An End-to-End Deep Learning Method for Solving Nonlocal Allen-Cahn and Cahn-Hilliard Phase-Field Models

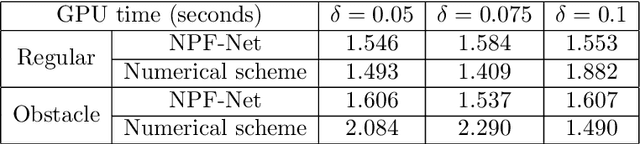
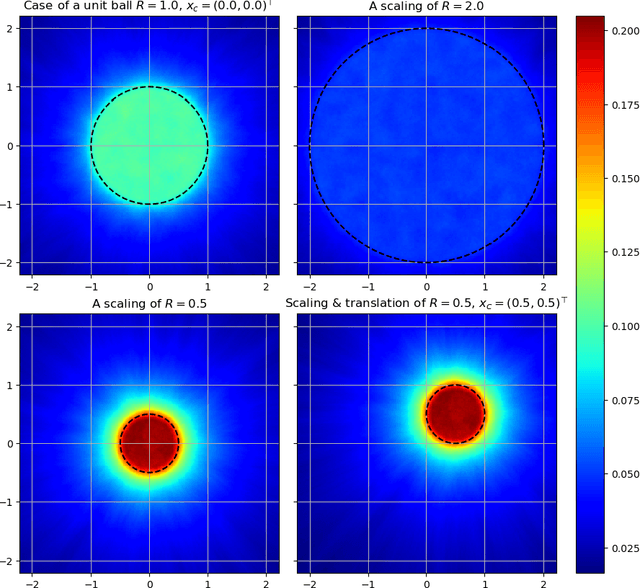
We propose an efficient end-to-end deep learning method for solving nonlocal Allen-Cahn (AC) and Cahn-Hilliard (CH) phase-field models. One motivation for this effort emanates from the fact that discretized partial differential equation-based AC or CH phase-field models result in diffuse interfaces between phases, with the only recourse for remediation is to severely refine the spatial grids in the vicinity of the true moving sharp interface whose width is determined by a grid-independent parameter that is substantially larger than the local grid size. In this work, we introduce non-mass conserving nonlocal AC or CH phase-field models with regular, logarithmic, or obstacle double-well potentials. Because of non-locality, some of these models feature totally sharp interfaces separating phases. The discretization of such models can lead to a transition between phases whose width is only a single grid cell wide. Another motivation is to use deep learning approaches to ameliorate the otherwise high cost of solving discretized nonlocal phase-field models. To this end, loss functions of the customized neural networks are defined using the residual of the fully discrete approximations of the AC or CH models, which results from applying a Fourier collocation method and a temporal semi-implicit approximation. To address the long-range interactions in the models, we tailor the architecture of the neural network by incorporating a nonlocal kernel as an input channel to the neural network model. We then provide the results of extensive computational experiments to illustrate the accuracy, structure-preserving properties, predictive capabilities, and cost reductions of the proposed method.

EfficientGS: Streamlining Gaussian Splatting for Large-Scale High-Resolution Scene Representation

In the domain of 3D scene representation, 3D Gaussian Splatting (3DGS) has emerged as a pivotal technology. However, its application to large-scale, high-resolution scenes (exceeding 4k$\times$4k pixels) is hindered by the excessive computational requirements for managing a large number of Gaussians. Addressing this, we introduce 'EfficientGS', an advanced approach that optimizes 3DGS for high-resolution, large-scale scenes. We analyze the densification process in 3DGS and identify areas of Gaussian over-proliferation. We propose a selective strategy, limiting Gaussian increase to key primitives, thereby enhancing the representational efficiency. Additionally, we develop a pruning mechanism to remove redundant Gaussians, those that are merely auxiliary to adjacent ones. For further enhancement, we integrate a sparse order increment for Spherical Harmonics (SH), designed to alleviate storage constraints and reduce training overhead. Our empirical evaluations, conducted on a range of datasets including extensive 4K+ aerial images, demonstrate that 'EfficientGS' not only expedites training and rendering times but also achieves this with a model size approximately tenfold smaller than conventional 3DGS while maintaining high rendering fidelity.

TransNet: Transferable Neural Networks for Partial Differential Equations

Transfer learning for partial differential equations (PDEs) is to develop a pre-trained neural network that can be used to solve a wide class of PDEs. Existing transfer learning approaches require much information of the target PDEs such as its formulation and/or data of its solution for pre-training. In this work, we propose to construct transferable neural feature spaces from purely function approximation perspectives without using PDE information. The construction of the feature space involves re-parameterization of the hidden neurons and uses auxiliary functions to tune the resulting feature space. Theoretical analysis shows the high quality of the produced feature space, i.e., uniformly distributed neurons. Extensive numerical experiments verify the outstanding performance of our method, including significantly improved transferability, e.g., using the same feature space for various PDEs with different domains and boundary conditions, and the superior accuracy, e.g., several orders of magnitude smaller mean squared error than the state of the art methods.

Style Mixing and Patchwise Prototypical Matching for One-Shot Unsupervised Domain Adaptive Semantic Segmentation

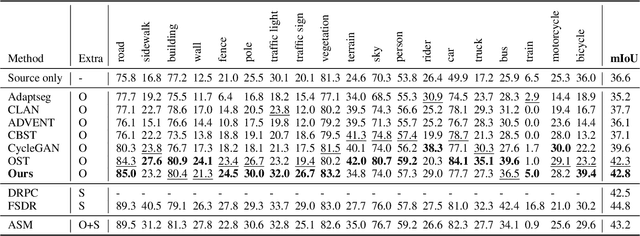
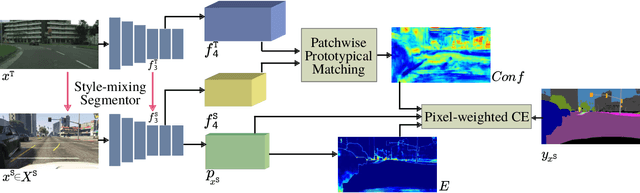
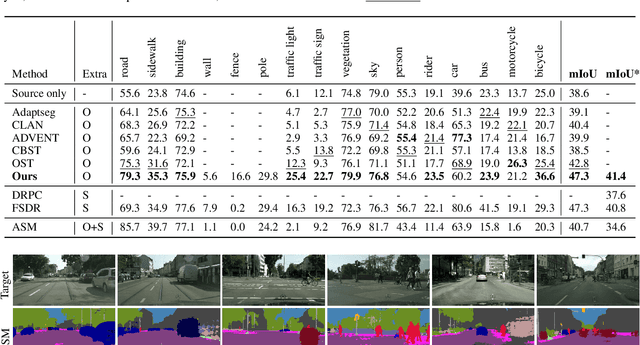
In this paper, we tackle the problem of one-shot unsupervised domain adaptation (OSUDA) for semantic segmentation where the segmentors only see one unlabeled target image during training. In this case, traditional unsupervised domain adaptation models usually fail since they cannot adapt to the target domain with over-fitting to one (or few) target samples. To address this problem, existing OSUDA methods usually integrate a style-transfer module to perform domain randomization based on the unlabeled target sample, with which multiple domains around the target sample can be explored during training. However, such a style-transfer module relies on an additional set of images as style reference for pre-training and also increases the memory demand for domain adaptation. Here we propose a new OSUDA method that can effectively relieve such computational burden. Specifically, we integrate several style-mixing layers into the segmentor which play the role of style-transfer module to stylize the source images without introducing any learned parameters. Moreover, we propose a patchwise prototypical matching (PPM) method to weighted consider the importance of source pixels during the supervised training to relieve the negative adaptation. Experimental results show that our method achieves new state-of-the-art performance on two commonly used benchmarks for domain adaptive semantic segmentation under the one-shot setting and is more efficient than all comparison approaches.

Level set learning with pseudo-reversible neural networks for nonlinear dimension reduction in function approximation

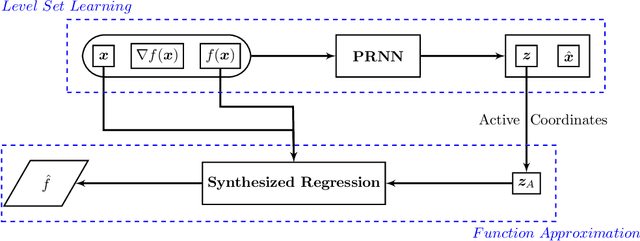
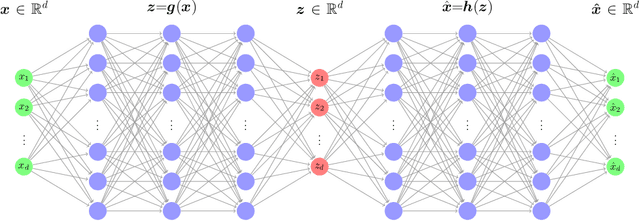
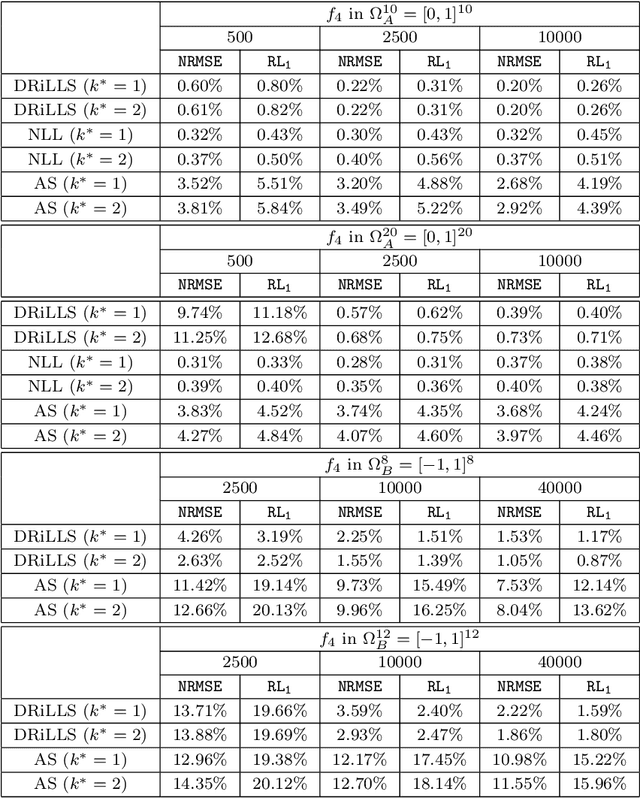
Due to the curse of dimensionality and the limitation on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method of Dimension Reduction via Learning Level Sets (DRiLLS) for function approximation. Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. The PRNN not only relaxes the invertibility constraint of the nonlinear transformation present in the NLL method due to the use of RevNet, but also adaptively weights the influence of each sample and controls the sensitivity of the function to the learned active variables. The synthesized regression uses Euclidean distance in the input space to select neighboring samples, whose projections on the space of active variables are used to perform local least-squares polynomial fitting. This helps to resolve numerical oscillation issues present in traditional local and global regressions. Extensive experimental results demonstrate that our DRiLLS method outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.

A Comparison of Neural Network Architectures for Data-Driven Reduced-Order Modeling

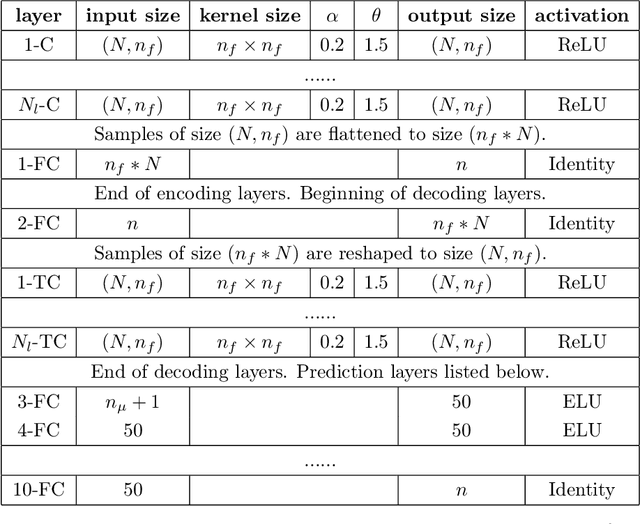
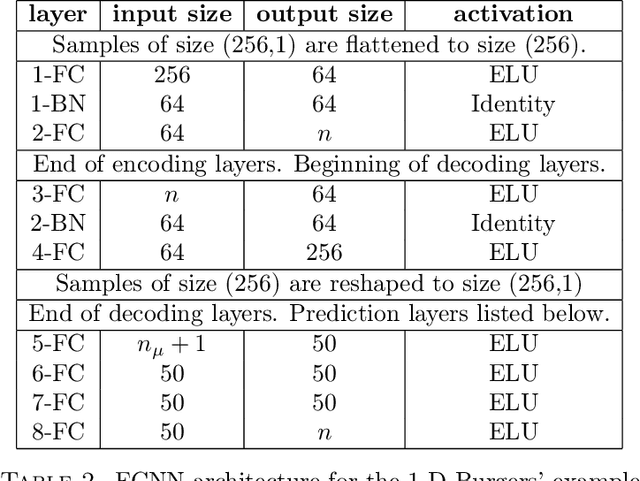
The popularity of deep convolutional autoencoders (CAEs) has engendered effective reduced-order models (ROMs) for the simulation of large-scale dynamical systems. However, it is not known whether deep CAEs provide superior performance in all ROM scenarios. To elucidate this, the effect of autoencoder architecture on its associated ROM is studied through the comparison of deep CAEs against two alternatives: a simple fully connected autoencoder, and a novel graph convolutional autoencoder. Through benchmark experiments, it is shown that the superior autoencoder architecture for a given ROM application is highly dependent on the size of the latent space and the structure of the snapshot data, with the proposed architecture demonstrating benefits on data with irregular connectivity when the latent space is sufficiently large.

Learning Green's Functions of Linear Reaction-Diffusion Equations with Application to Fast Numerical Solver

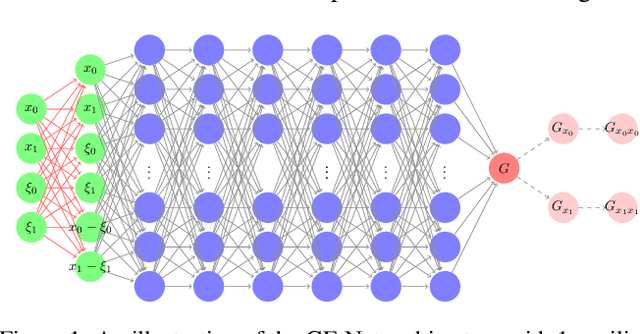
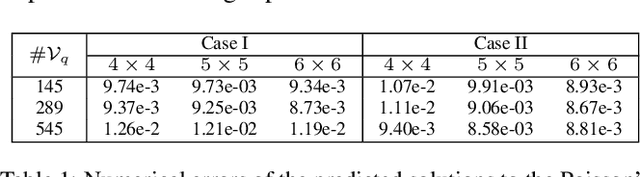
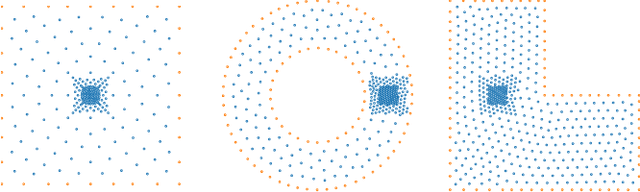
Partial differential equations are often used to model various physical phenomena, such as heat diffusion, wave propagation, fluid dynamics, elasticity, electrodynamics and image processing, and many analytic approaches or traditional numerical methods have been developed and widely used for their solutions. Inspired by rapidly growing impact of deep learning on scientific and engineering research, in this paper we propose a novel neural network, GF-Net, for learning the Green's functions of linear reaction-diffusion equations in an unsupervised fashion. The proposed method overcomes the challenges for finding the Green's functions of the equations on arbitrary domains by utilizing physics-informed approach and the symmetry of the Green's function. As a consequence, it particularly leads to an efficient way for solving the target equations under different boundary conditions and sources. We also demonstrate the effectiveness of the proposed approach by experiments in square, annular and L-shape domains.