WgLaSDI: Weak-Form Greedy Latent Space Dynamics Identification

The parametric greedy latent space dynamics identification (gLaSDI) framework has demonstrated promising potential for accurate and efficient modeling of high-dimensional nonlinear physical systems. However, it remains challenging to handle noisy data. To enhance robustness against noise, we incorporate the weak-form estimation of nonlinear dynamics (WENDy) into gLaSDI. In the proposed weak-form gLaSDI (WgLaSDI) framework, an autoencoder and WENDy are trained simultaneously to discover intrinsic nonlinear latent-space dynamics of high-dimensional data. Compared to the standard sparse identification of nonlinear dynamics (SINDy) employed in gLaSDI, WENDy enables variance reduction and robust latent space discovery, therefore leading to more accurate and efficient reduced-order modeling. Furthermore, the greedy physics-informed active learning in WgLaSDI enables adaptive sampling of optimal training data on the fly for enhanced modeling accuracy. The effectiveness of the proposed framework is demonstrated by modeling various nonlinear dynamical problems, including viscous and inviscid Burgers' equations, time-dependent radial advection, and the Vlasov equation for plasma physics. With data that contains 5-10% Gaussian white noise, WgLaSDI outperforms gLaSDI by orders of magnitude, achieving 1-7% relative errors. Compared with the high-fidelity models, WgLaSDI achieves 121 to 1,779x speed-up.

A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling

Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.

Weak-Form Latent Space Dynamics Identification

Recent work in data-driven modeling has demonstrated that a weak formulation of model equations enhances the noise robustness of a wide range of computational methods. In this paper, we demonstrate the power of the weak form to enhance the LaSDI (Latent Space Dynamics Identification) algorithm, a recently developed data-driven reduced order modeling technique. We introduce a weak form-based version WLaSDI (Weak-form Latent Space Dynamics Identification). WLaSDI first compresses data, then projects onto the test functions and learns the local latent space models. Notably, WLaSDI demonstrates significantly enhanced robustness to noise. With WLaSDI, the local latent space is obtained using weak-form equation learning techniques. Compared to the standard sparse identification of nonlinear dynamics (SINDy) used in LaSDI, the variance reduction of the weak form guarantees a robust and precise latent space recovery, hence allowing for a fast, robust, and accurate simulation. We demonstrate the efficacy of WLaSDI vs. LaSDI on several common benchmark examples including viscid and inviscid Burgers', radial advection, and heat conduction. For instance, in the case of 1D inviscid Burgers' simulations with the addition of up to 100% Gaussian white noise, the relative error remains consistently below 6% for WLaSDI, while it can exceed 10,000% for LaSDI. Similarly, for radial advection simulations, the relative errors stay below 15% for WLaSDI, in stark contrast to the potential errors of up to 10,000% with LaSDI. Moreover, speedups of several orders of magnitude can be obtained with WLaSDI. For example applying WLaSDI to 1D Burgers' yields a 140X speedup compared to the corresponding full order model. Python code to reproduce the results in this work is available at (https://github.com/MathBioCU/PyWSINDy_ODE) and (https://github.com/MathBioCU/PyWLaSDI).

Data-Driven Modeling of an Unsaturated Bentonite Buffer Model Test Under High Temperatures Using an Enhanced Axisymmetric Reproducing Kernel Particle Method

In deep geological repositories for high level nuclear waste with close canister spacings, bentonite buffers can experience temperatures higher than 100 {\deg}C. In this range of extreme temperatures, phenomenological constitutive laws face limitations in capturing the thermo-hydro-mechanical (THM) behavior of the bentonite, since the pre-defined functional constitutive laws often lack generality and flexibility to capture a wide range of complex coupling phenomena as well as the effects of stress state and path dependency. In this work, a deep neural network (DNN)-based soil-water retention curve (SWRC) of bentonite is introduced and integrated into a Reproducing Kernel Particle Method (RKPM) for conducting THM simulations of the bentonite buffer. The DNN-SWRC model incorporates temperature as an additional input variable, allowing it to learn the relationship between suction and degree of saturation under the general non-isothermal condition, which is difficult to represent using a phenomenological SWRC. For effective modeling of the tank-scale test, new axisymmetric Reproducing Kernel basis functions enriched with singular Dirichlet enforcement representing heater placement and an effective convective heat transfer coefficient representing thin-layer composite tank construction are developed. The proposed method is demonstrated through the modeling of a tank-scale experiment involving a cylindrical layer of MX-80 bentonite exposed to central heating.

A Multi-Resolution Physics-Informed Recurrent Neural Network: Formulation and Application to Musculoskeletal Systems

This work presents a multi-resolution physics-informed recurrent neural network (MR PI-RNN), for simultaneous prediction of musculoskeletal (MSK) motion and parameter identification of the MSK systems. The MSK application was selected as the model problem due to its challenging nature in mapping the high-frequency surface electromyography (sEMG) signals to the low-frequency body joint motion controlled by the MSK and muscle contraction dynamics. The proposed method utilizes the fast wavelet transform to decompose the mixed frequency input sEMG and output joint motion signals into nested multi-resolution signals. The prediction model is subsequently trained on coarser-scale input-output signals using a gated recurrent unit (GRU), and then the trained parameters are transferred to the next level of training with finer-scale signals. These training processes are repeated recursively under a transfer-learning fashion until the full-scale training (i.e., with unfiltered signals) is achieved, while satisfying the underlying dynamic equilibrium. Numerical examples on recorded subject data demonstrate the effectiveness of the proposed framework in generating a physics-informed forward-dynamics surrogate, which yields higher accuracy in motion predictions of elbow flexion-extension of an MSK system compared to the case with single-scale training. The framework is also capable of identifying muscle parameters that are physiologically consistent with the subject's kinematics data.

Certified data-driven physics-informed greedy auto-encoder simulator

A parametric adaptive greedy Latent Space Dynamics Identification (gLaSDI) framework is developed for accurate, efficient, and certified data-driven physics-informed greedy auto-encoder simulators of high-dimensional nonlinear dynamical systems. In the proposed framework, an auto-encoder and dynamics identification models are trained interactively to discover intrinsic and simple latent-space dynamics. To effectively explore the parameter space for optimal model performance, an adaptive greedy sampling algorithm integrated with a physics-informed error indicator is introduced to search for optimal training samples on the fly, outperforming the conventional predefined uniform sampling. Further, an efficient k-nearest neighbor convex interpolation scheme is employed to exploit local latent-space dynamics for improved predictability. Numerical results demonstrate that the proposed method achieves 121 to 2,658x speed-up with 1 to 5% relative errors for radial advection and 2D Burgers dynamical problems.

Deep autoencoders for physics-constrained data-driven nonlinear materials modeling

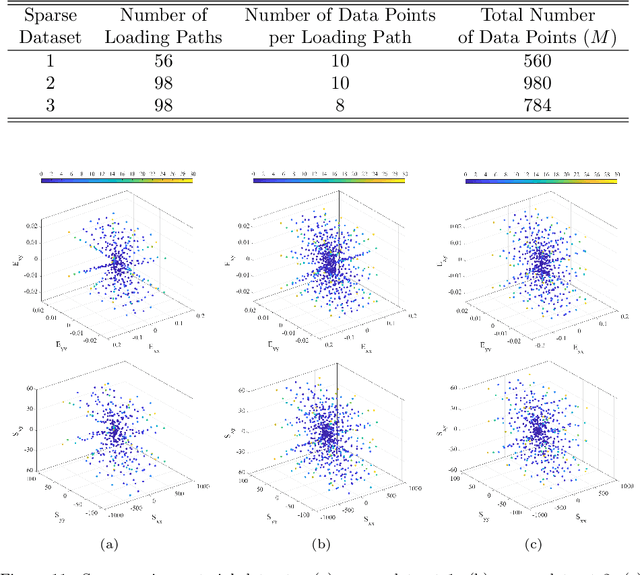
Physics-constrained data-driven computing is an emerging computational paradigm that allows simulation of complex materials directly based on material database and bypass the classical constitutive model construction. However, it remains difficult to deal with high-dimensional applications and extrapolative generalization. This paper introduces deep learning techniques under the data-driven framework to address these fundamental issues in nonlinear materials modeling. To this end, an autoencoder neural network architecture is introduced to learn the underlying low-dimensional representation (embedding) of the given material database. The offline trained autoencoder and the discovered embedding space are then incorporated in the online data-driven computation such that the search of optimal material state from database can be performed on a low-dimensional space, aiming to enhance the robustness and predictability with projected material data. To ensure numerical stability and representative constitutive manifold, a convexity-preserving interpolation scheme tailored to the proposed autoencoder-based data-driven solver is proposed for constructing the material state. In this study, the applicability of the proposed approach is demonstrated by modeling nonlinear biological tissues. A parametric study on data noise, data size and sparsity, training initialization, and model architectures, is also conducted to examine the robustness and convergence property of the proposed approach.

Thermodynamically Consistent Machine-Learned Internal State Variable Approach for Data-Driven Modeling of Path-Dependent Materials

Characterization and modeling of path-dependent behaviors of complex materials by phenomenological models remains challenging due to difficulties in formulating mathematical expressions and internal state variables (ISVs) governing path-dependent behaviors. Data-driven machine learning models, such as deep neural networks and recurrent neural networks (RNNs), have become viable alternatives. However, pure black-box data-driven models mapping inputs to outputs without considering the underlying physics suffer from unstable and inaccurate generalization performance. This study proposes a machine-learned physics-informed data-driven constitutive modeling approach for path-dependent materials based on the measurable material states. The proposed data-driven constitutive model is designed with the consideration of universal thermodynamics principles, where the ISVs essential to the material path-dependency are inferred automatically from the hidden state of RNNs. The RNN describing the evolution of the data-driven machine-learned ISVs follows the thermodynamics second law. To enhance the robustness and accuracy of RNN models, stochasticity is introduced to model training. The effects of the number of RNN history steps, the internal state dimension, the model complexity, and the strain increment on model performances have been investigated. The effectiveness of the proposed method is evaluated by modeling soil material behaviors under cyclic shear loading using experimental stress-strain data.

gLaSDI: Parametric Physics-informed Greedy Latent Space Dynamics Identification

A parametric adaptive physics-informed greedy Latent Space Dynamics Identification (gLaSDI) method is proposed for accurate, efficient, and robust data-driven reduced-order modeling of high-dimensional nonlinear dynamical systems. In the proposed gLaSDI framework, an autoencoder discovers intrinsic nonlinear latent representations of high-dimensional data, while dynamics identification (DI) models capture local latent-space dynamics. An interactive training algorithm is adopted for the autoencoder and local DI models, which enables identification of simple latent-space dynamics and enhances accuracy and efficiency of data-driven reduced-order modeling. To maximize and accelerate the exploration of the parameter space for the optimal model performance, an adaptive greedy sampling algorithm integrated with a physics-informed residual-based error indicator and random-subset evaluation is introduced to search for the optimal training samples on-the-fly. Further, to exploit local latent-space dynamics captured by the local DI models for an improved modeling accuracy with a minimum number of local DI models in the parameter space, an efficient k-nearest neighbor convex interpolation scheme is employed. The effectiveness of the proposed framework is demonstrated by modeling various nonlinear dynamical problems, including Burgers equations, nonlinear heat conduction, and radial advection. The proposed adaptive greedy sampling outperforms the conventional predefined uniform sampling in terms of accuracy. Compared with the high-fidelity models, gLaSDI achieves 66 to 4,417x speed-up with 1 to 5% relative errors.