N-Adaptive Ritz Method: A Neural Network Enriched Partition of Unity for Boundary Value Problems

Conventional finite element methods are known to be tedious in adaptive refinements due to their conformal regularity requirements. Further, the enrichment functions for adaptive refinements are often not readily available in general applications. This work introduces a novel neural network-enriched Partition of Unity (NN-PU) approach for solving boundary value problems via artificial neural networks with a potential energy-based loss function minimization. The flexibility and adaptivity of the NN function space are utilized to capture complex solution patterns that the conventional Galerkin methods fail to capture. The NN enrichment is constructed by combining pre-trained feature-encoded NN blocks with an additional untrained NN block. The pre-trained NN blocks learn specific local features during the offline stage, enabling efficient enrichment of the approximation space during the online stage through the Ritz-type energy minimization. The NN enrichment is introduced under the Partition of Unity (PU) framework, ensuring convergence of the proposed method. The proposed NN-PU approximation and feature-encoded transfer learning forms an adaptive approximation framework, termed the neural-refinement (n-refinement), for solving boundary value problems. Demonstrated by solving various elasticity problems, the proposed method offers accurate solutions while notably reducing the computational cost compared to the conventional adaptive refinement in the mesh-based methods.

Data-Driven Modeling of an Unsaturated Bentonite Buffer Model Test Under High Temperatures Using an Enhanced Axisymmetric Reproducing Kernel Particle Method

In deep geological repositories for high level nuclear waste with close canister spacings, bentonite buffers can experience temperatures higher than 100 {\deg}C. In this range of extreme temperatures, phenomenological constitutive laws face limitations in capturing the thermo-hydro-mechanical (THM) behavior of the bentonite, since the pre-defined functional constitutive laws often lack generality and flexibility to capture a wide range of complex coupling phenomena as well as the effects of stress state and path dependency. In this work, a deep neural network (DNN)-based soil-water retention curve (SWRC) of bentonite is introduced and integrated into a Reproducing Kernel Particle Method (RKPM) for conducting THM simulations of the bentonite buffer. The DNN-SWRC model incorporates temperature as an additional input variable, allowing it to learn the relationship between suction and degree of saturation under the general non-isothermal condition, which is difficult to represent using a phenomenological SWRC. For effective modeling of the tank-scale test, new axisymmetric Reproducing Kernel basis functions enriched with singular Dirichlet enforcement representing heater placement and an effective convective heat transfer coefficient representing thin-layer composite tank construction are developed. The proposed method is demonstrated through the modeling of a tank-scale experiment involving a cylindrical layer of MX-80 bentonite exposed to central heating.

A Neural Network-Based Enrichment of Reproducing Kernel Approximation for Modeling Brittle Fracture

Numerical modeling of localizations is a challenging task due to the evolving rough solution in which the localization paths are not predefined. Despite decades of efforts, there is a need for innovative discretization-independent computational methods to predict the evolution of localizations. In this work, an improved version of the neural network-enhanced Reproducing Kernel Particle Method (NN-RKPM) is proposed for modeling brittle fracture. In the proposed method, a background reproducing kernel (RK) approximation defined on a coarse and uniform discretization is enriched by a neural network (NN) approximation under a Partition of Unity framework. In the NN approximation, the deep neural network automatically locates and inserts regularized discontinuities in the function space. The NN-based enrichment functions are then patched together with RK approximation functions using RK as a Partition of Unity patching function. The optimum NN parameters defining the location, orientation, and displacement distribution across location together with RK approximation coefficients are obtained via the energy-based loss function minimization. To regularize the NN-RK approximation, a constraint on the spatial gradient of the parametric coordinates is imposed in the loss function. Analysis of the convergence properties shows that the solution convergence of the proposed method is guaranteed. The effectiveness of the proposed method is demonstrated by a series of numerical examples involving damage propagation and branching.

Support Vector Machine Guided Reproducing Kernel Particle Method for Image-Based Modeling of Microstructures

This work presents an approach for automating the discretization and approximation procedures in constructing digital representations of composites from Micro-CT images featuring intricate microstructures. The proposed method is guided by the Support Vector Machine (SVM) classification, offering an effective approach for discretizing microstructural images. An SVM soft margin training process is introduced as a classification of heterogeneous material points, and image segmentation is accomplished by identifying support vectors through a local regularized optimization problem. In addition, an Interface-Modified Reproducing Kernel Particle Method (IM-RKPM) is proposed for appropriate approximations of weak discontinuities across material interfaces. The proposed method modifies the smooth kernel functions with a regularized heavy-side function concerning the material interfaces to alleviate Gibb's oscillations. This IM-RKPM is formulated without introducing duplicated degrees of freedom associated with the interface nodes commonly needed in the conventional treatments of weak discontinuities in the meshfree methods. Moreover, IM-RKPM can be implemented with various domain integration techniques, such as Stabilized Conforming Nodal Integration (SCNI). The extension of the proposed method to 3-dimension is straightforward, and the effectiveness of the proposed method is validated through the image-based modeling of polymer-ceramic composite microstructures.

A Neural Network-enhanced Reproducing Kernel Particle Method for Modeling Strain Localization

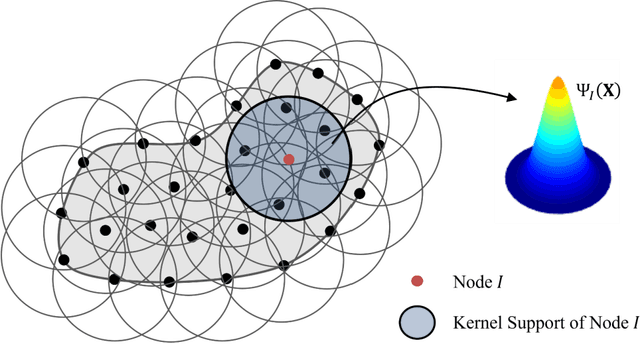
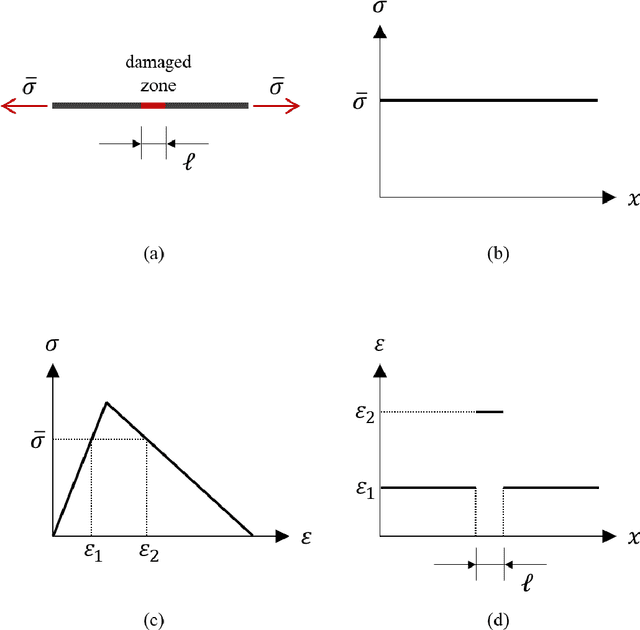
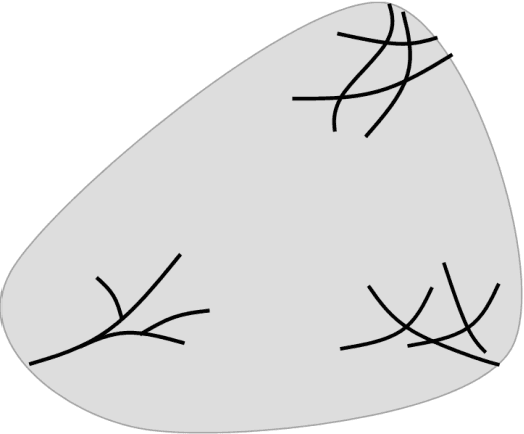
Modeling the localized intensive deformation in a damaged solid requires highly refined discretization for accurate prediction, which significantly increases the computational cost. Although adaptive model refinement can be employed for enhanced effectiveness, it is cumbersome for the traditional mesh-based methods to perform while modeling the evolving localizations. In this work, neural network-enhanced reproducing kernel particle method (NN-RKPM) is proposed, where the location, orientation, and shape of the solution transition near a localization is automatically captured by the NN approximation via a block-level neural network optimization. The weights and biases in the blocked parametrization network control the location and orientation of the localization. The designed basic four-kernel NN block is capable of capturing a triple junction or a quadruple junction topological pattern, while more complicated localization topological patters are captured by the superposition of multiple four-kernel NN blocks. The standard RK approximation is then utilized to approximate the smooth part of the solution, which permits a much coarser discretization than the high-resolution discretization needed to capture sharp solution transitions with the conventional methods. A regularization of the neural network approximation is additionally introduced for discretization-independent material responses. The effectiveness of the proposed NN-RKPM is verified by a series of numerical verifications.