Accelerating Phase Field Simulations Through a Hybrid Adaptive Fourier Neural Operator with U-Net Backbone

Prolonged contact between a corrosive liquid and metal alloys can cause progressive dealloying. For such liquid-metal dealloying (LMD) process, phase field models have been developed. However, the governing equations often involve coupled non-linear partial differential equations (PDE), which are challenging to solve numerically. In particular, stiffness in the PDEs requires an extremely small time steps (e.g. $10^{-12}$ or smaller). This computational bottleneck is especially problematic when running LMD simulation until a late time horizon is required. This motivates the development of surrogate models capable of leaping forward in time, by skipping several consecutive time steps at-once. In this paper, we propose U-Shaped Adaptive Fourier Neural Operators (U-AFNO), a machine learning (ML) model inspired by recent advances in neural operator learning. U-AFNO employs U-Nets for extracting and reconstructing local features within the physical fields, and passes the latent space through a vision transformer (ViT) implemented in the Fourier space (AFNO). We use U-AFNOs to learn the dynamics mapping the field at a current time step into a later time step. We also identify global quantities of interest (QoI) describing the corrosion process (e.g. the deformation of the liquid-metal interface) and show that our proposed U-AFNO model is able to accurately predict the field dynamics, in-spite of the chaotic nature of LMD. Our model reproduces the key micro-structure statistics and QoIs with a level of accuracy on-par with the high-fidelity numerical solver. We also investigate the opportunity of using hybrid simulations, in which we alternate forward leap in time using the U-AFNO with high-fidelity time stepping. We demonstrate that while advantageous for some surrogate model design choices, our proposed U-AFNO model in fully auto-regressive settings consistently outperforms hybrid schemes.

A Comprehensive Review of Latent Space Dynamics Identification Algorithms for Intrusive and Non-Intrusive Reduced-Order-Modeling

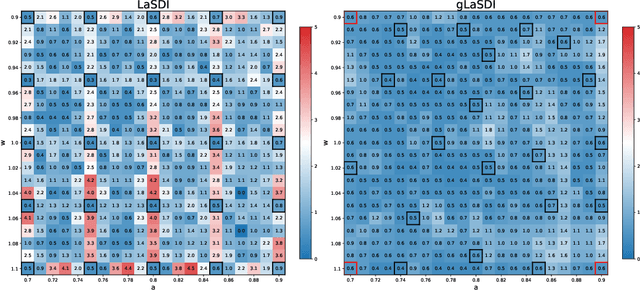
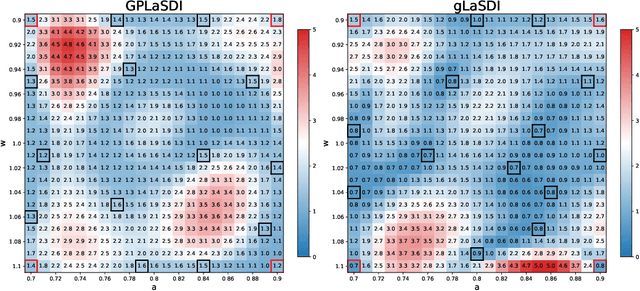
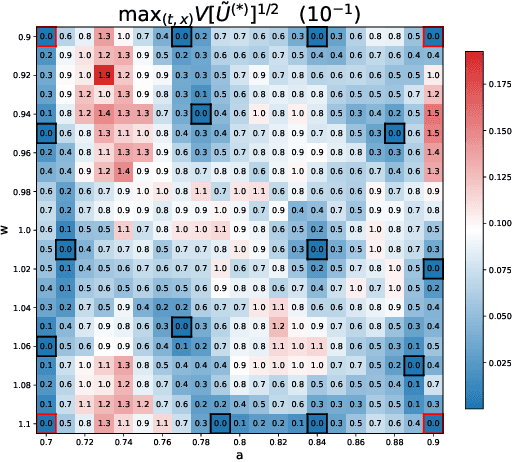
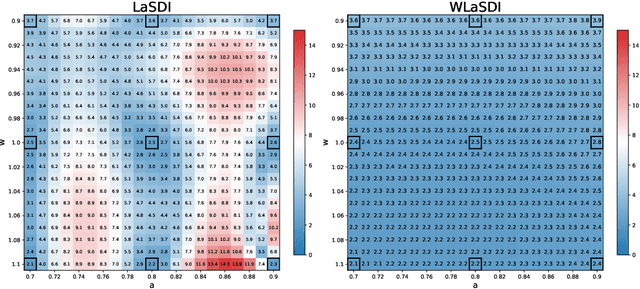
Numerical solvers of partial differential equations (PDEs) have been widely employed for simulating physical systems. However, the computational cost remains a major bottleneck in various scientific and engineering applications, which has motivated the development of reduced-order models (ROMs). Recently, machine-learning-based ROMs have gained significant popularity and are promising for addressing some limitations of traditional ROM methods, especially for advection dominated systems. In this chapter, we focus on a particular framework known as Latent Space Dynamics Identification (LaSDI), which transforms the high-fidelity data, governed by a PDE, to simpler and low-dimensional latent-space data, governed by ordinary differential equations (ODEs). These ODEs can be learned and subsequently interpolated to make ROM predictions. Each building block of LaSDI can be easily modulated depending on the application, which makes the LaSDI framework highly flexible. In particular, we present strategies to enforce the laws of thermodynamics into LaSDI models (tLaSDI), enhance robustness in the presence of noise through the weak form (WLaSDI), select high-fidelity training data efficiently through active learning (gLaSDI, GPLaSDI), and quantify the ROM prediction uncertainty through Gaussian processes (GPLaSDI). We demonstrate the performance of different LaSDI approaches on Burgers equation, a non-linear heat conduction problem, and a plasma physics problem, showing that LaSDI algorithms can achieve relative errors of less than a few percent and up to thousands of times speed-ups.

Data-Driven Autoencoder Numerical Solver with Uncertainty Quantification for Fast Physical Simulations

Traditional partial differential equation (PDE) solvers can be computationally expensive, which motivates the development of faster methods, such as reduced-order-models (ROMs). We present GPLaSDI, a hybrid deep-learning and Bayesian ROM. GPLaSDI trains an autoencoder on full-order-model (FOM) data and simultaneously learns simpler equations governing the latent space. These equations are interpolated with Gaussian Processes, allowing for uncertainty quantification and active learning, even with limited access to the FOM solver. Our framework is able to achieve up to 100,000 times speed-up and less than 7% relative error on fluid mechanics problems.

GPLaSDI: Gaussian Process-based Interpretable Latent Space Dynamics Identification through Deep Autoencoder

Numerically solving partial differential equations (PDEs) can be challenging and computationally expensive. This has led to the development of reduced-order models (ROMs) that are accurate but faster than full order models (FOMs). Recently, machine learning advances have enabled the creation of non-linear projection methods, such as Latent Space Dynamics Identification (LaSDI). LaSDI maps full-order PDE solutions to a latent space using autoencoders and learns the system of ODEs governing the latent space dynamics. By interpolating and solving the ODE system in the reduced latent space, fast and accurate ROM predictions can be made by feeding the predicted latent space dynamics into the decoder. In this paper, we introduce GPLaSDI, a novel LaSDI-based framework that relies on Gaussian process (GP) for latent space ODE interpolations. Using GPs offers two significant advantages. First, it enables the quantification of uncertainty over the ROM predictions. Second, leveraging this prediction uncertainty allows for efficient adaptive training through a greedy selection of additional training data points. This approach does not require prior knowledge of the underlying PDEs. Consequently, GPLaSDI is inherently non-intrusive and can be applied to problems without a known PDE or its residual. We demonstrate the effectiveness of our approach on the Burgers equation, Vlasov equation for plasma physics, and a rising thermal bubble problem. Our proposed method achieves between 200 and 100,000 times speed-up, with up to 7% relative error.

Bayesian Deep Learning for Partial Differential Equation Parameter Discovery with Sparse and Noisy Data

Scientific machine learning has been successfully applied to inverse problems and PDE discoveries in computational physics. One caveat of current methods however is the need for large amounts of (clean) data in order to recover full system responses or underlying physical models. Bayesian methods may be particularly promising to overcome these challenges as they are naturally less sensitive to sparse and noisy data. In this paper, we propose to use Bayesian neural networks (BNN) in order to: 1) Recover the full system states from measurement data (e.g. temperature, velocity field, etc.). We use Hamiltonian Monte-Carlo to sample the posterior distribution of a deep and dense BNN, and show that it is possible to accurately capture physics of varying complexity without overfitting. 2) Recover the parameters in the underlying partial differential equation (PDE) governing the physical system. Using the trained BNN as a surrogate of the system response, we generate datasets of derivatives potentially comprising the latent PDE of the observed system and perform a Bayesian linear regression (BLR) between the successive derivatives in space and time to recover the original PDE parameters. We take advantage of the confidence intervals on the BNN outputs and introduce the spatial derivative variance into the BLR likelihood to discard the influence of highly uncertain surrogate data points, which allows for more accurate parameter discovery. We demonstrate our approach on a handful of example applied to physics and non-linear dynamics.