Accelerating Phase Field Simulations Through a Hybrid Adaptive Fourier Neural Operator with U-Net Backbone

Prolonged contact between a corrosive liquid and metal alloys can cause progressive dealloying. For such liquid-metal dealloying (LMD) process, phase field models have been developed. However, the governing equations often involve coupled non-linear partial differential equations (PDE), which are challenging to solve numerically. In particular, stiffness in the PDEs requires an extremely small time steps (e.g. $10^{-12}$ or smaller). This computational bottleneck is especially problematic when running LMD simulation until a late time horizon is required. This motivates the development of surrogate models capable of leaping forward in time, by skipping several consecutive time steps at-once. In this paper, we propose U-Shaped Adaptive Fourier Neural Operators (U-AFNO), a machine learning (ML) model inspired by recent advances in neural operator learning. U-AFNO employs U-Nets for extracting and reconstructing local features within the physical fields, and passes the latent space through a vision transformer (ViT) implemented in the Fourier space (AFNO). We use U-AFNOs to learn the dynamics mapping the field at a current time step into a later time step. We also identify global quantities of interest (QoI) describing the corrosion process (e.g. the deformation of the liquid-metal interface) and show that our proposed U-AFNO model is able to accurately predict the field dynamics, in-spite of the chaotic nature of LMD. Our model reproduces the key micro-structure statistics and QoIs with a level of accuracy on-par with the high-fidelity numerical solver. We also investigate the opportunity of using hybrid simulations, in which we alternate forward leap in time using the U-AFNO with high-fidelity time stepping. We demonstrate that while advantageous for some surrogate model design choices, our proposed U-AFNO model in fully auto-regressive settings consistently outperforms hybrid schemes.

Bayesian optimization for stable properties amid processing fluctuations in sputter deposition

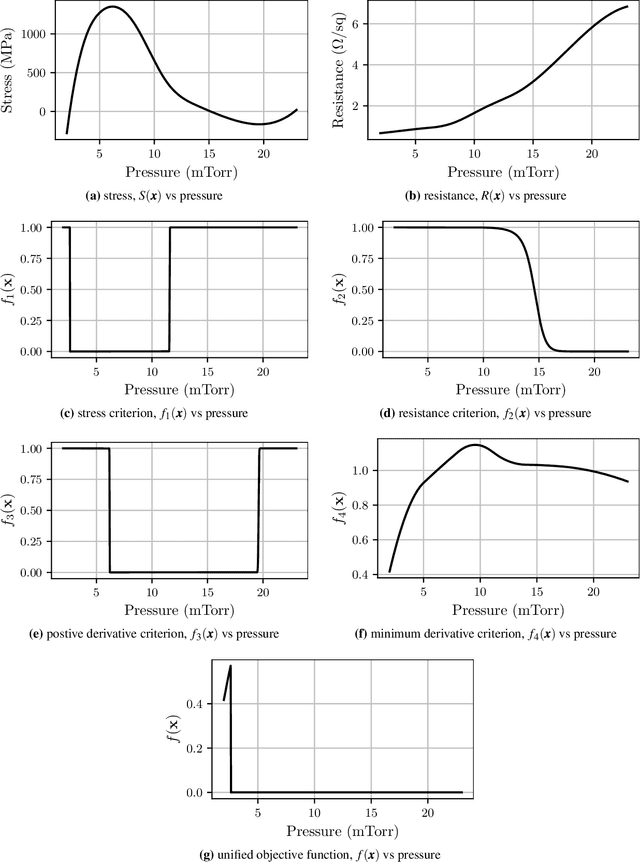
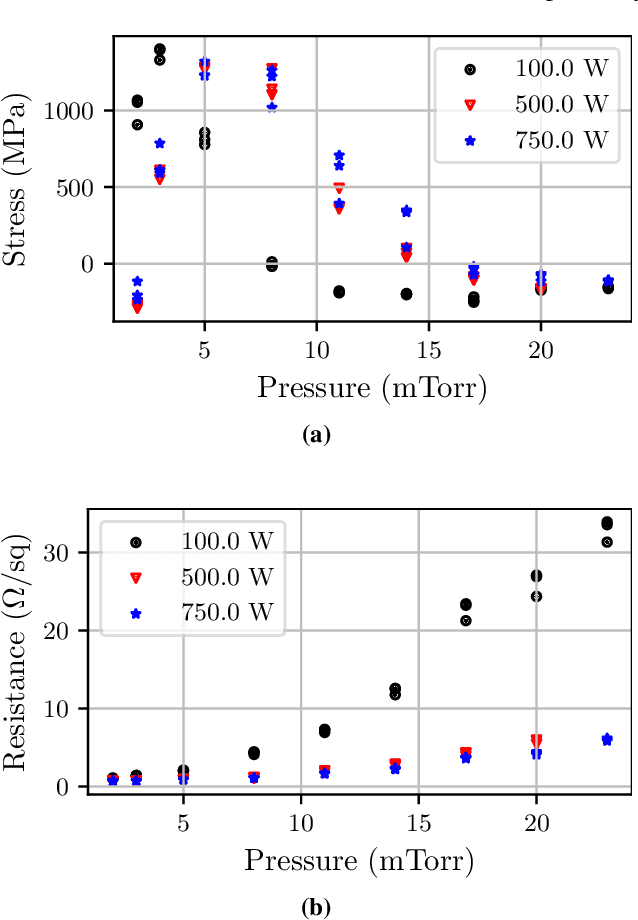
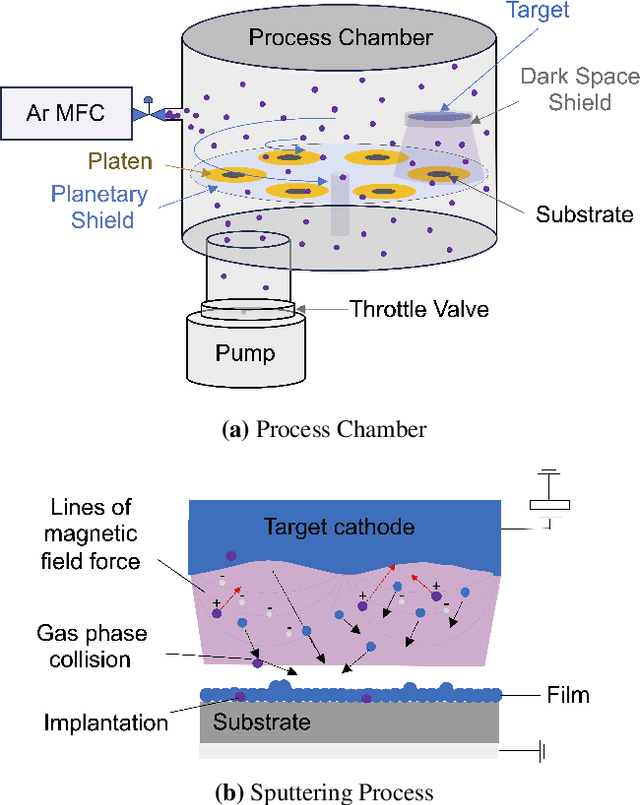
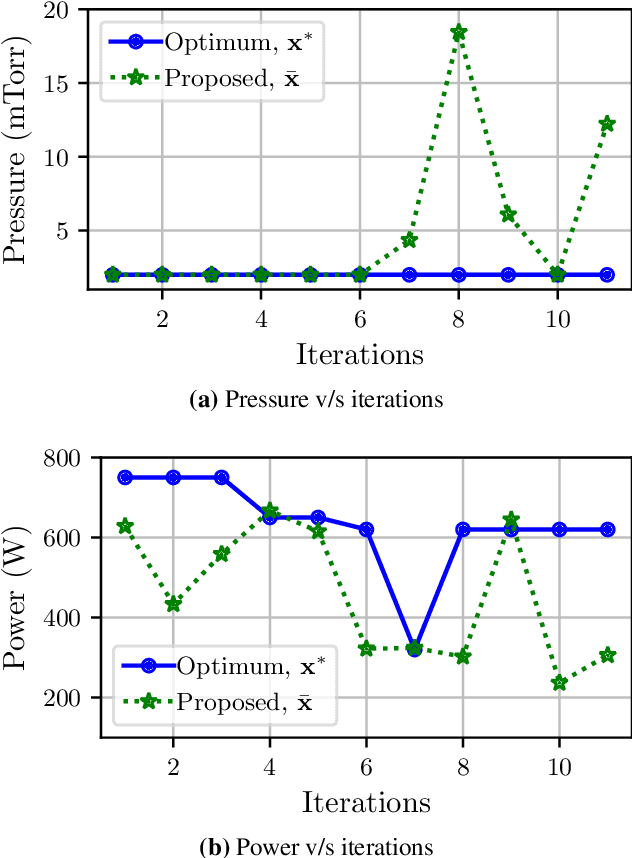
We introduce a Bayesian optimization approach to guide the sputter deposition of molybdenum thin films, aiming to achieve desired residual stress and sheet resistance while minimizing susceptibility to stochastic fluctuations during deposition. Thin films are pivotal in numerous technologies, including semiconductors and optical devices, where their properties are critical. Sputter deposition parameters, such as deposition power, vacuum chamber pressure, and working distance, influence physical properties like residual stress and resistance. Excessive stress and high resistance can impair device performance, necessitating the selection of optimal process parameters. Furthermore, these parameters should ensure the consistency and reliability of thin film properties, assisting in the reproducibility of the devices. However, exploring the multidimensional design space for process optimization is expensive. Bayesian optimization is ideal for optimizing inputs/parameters of general black-box functions without reliance on gradient information. We utilize Bayesian optimization to optimize deposition power and pressure using a custom-built objective function incorporating observed stress and resistance data. Additionally, we integrate prior knowledge of stress variation with pressure into the objective function to prioritize films least affected by stochastic variations. Our findings demonstrate that Bayesian optimization effectively explores the design space and identifies optimal parameter combinations meeting desired stress and resistance specifications.

Polynomial Chaos Surrogate Construction for Random Fields with Parametric Uncertainty

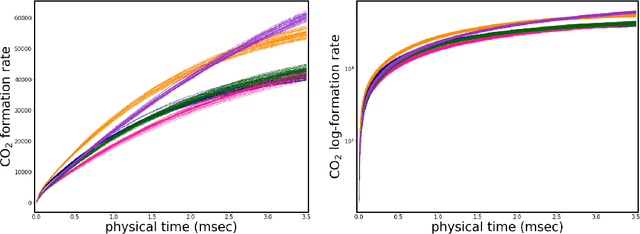
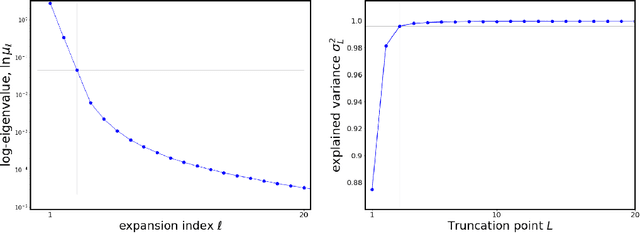
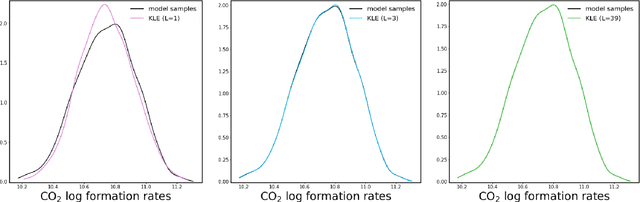
Engineering and applied science rely on computational experiments to rigorously study physical systems. The mathematical models used to probe these systems are highly complex, and sampling-intensive studies often require prohibitively many simulations for acceptable accuracy. Surrogate models provide a means of circumventing the high computational expense of sampling such complex models. In particular, polynomial chaos expansions (PCEs) have been successfully used for uncertainty quantification studies of deterministic models where the dominant source of uncertainty is parametric. We discuss an extension to conventional PCE surrogate modeling to enable surrogate construction for stochastic computational models that have intrinsic noise in addition to parametric uncertainty. We develop a PCE surrogate on a joint space of intrinsic and parametric uncertainty, enabled by Rosenblatt transformations, and then extend the construction to random field data via the Karhunen-Loeve expansion. We then take advantage of closed-form solutions for computing PCE Sobol indices to perform a global sensitivity analysis of the model which quantifies the intrinsic noise contribution to the overall model output variance. Additionally, the resulting joint PCE is generative in the sense that it allows generating random realizations at any input parameter setting that are statistically approximately equivalent to realizations from the underlying stochastic model. The method is demonstrated on a chemical catalysis example model.

Compressive sensing adaptation for polynomial chaos expansions

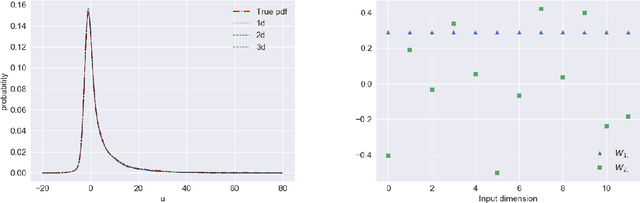
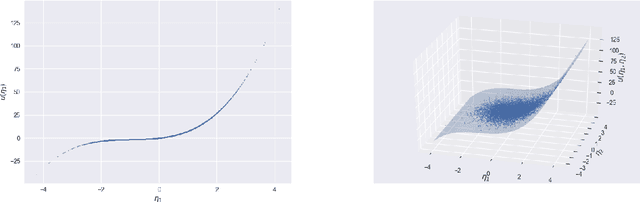
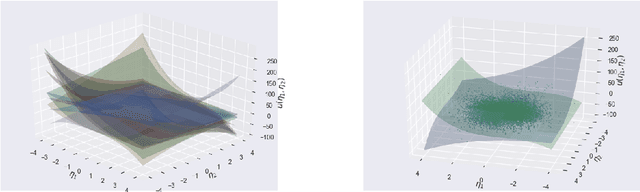
Basis adaptation in Homogeneous Chaos spaces rely on a suitable rotation of the underlying Gaussian germ. Several rotations have been proposed in the literature resulting in adaptations with different convergence properties. In this paper we present a new adaptation mechanism that builds on compressive sensing algorithms, resulting in a reduced polynomial chaos approximation with optimal sparsity. The developed adaptation algorithm consists of a two-step optimization procedure that computes the optimal coefficients and the input projection matrix of a low dimensional chaos expansion with respect to an optimally rotated basis. We demonstrate the attractive features of our algorithm through several numerical examples including the application on Large-Eddy Simulation (LES) calculations of turbulent combustion in a HIFiRE scramjet engine.