Bayesian optimization for stable properties amid processing fluctuations in sputter deposition

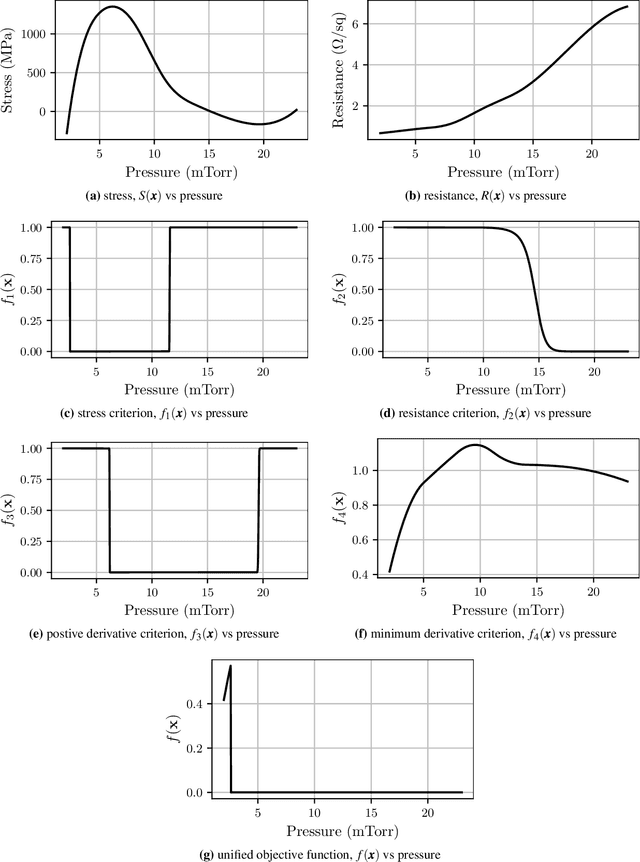
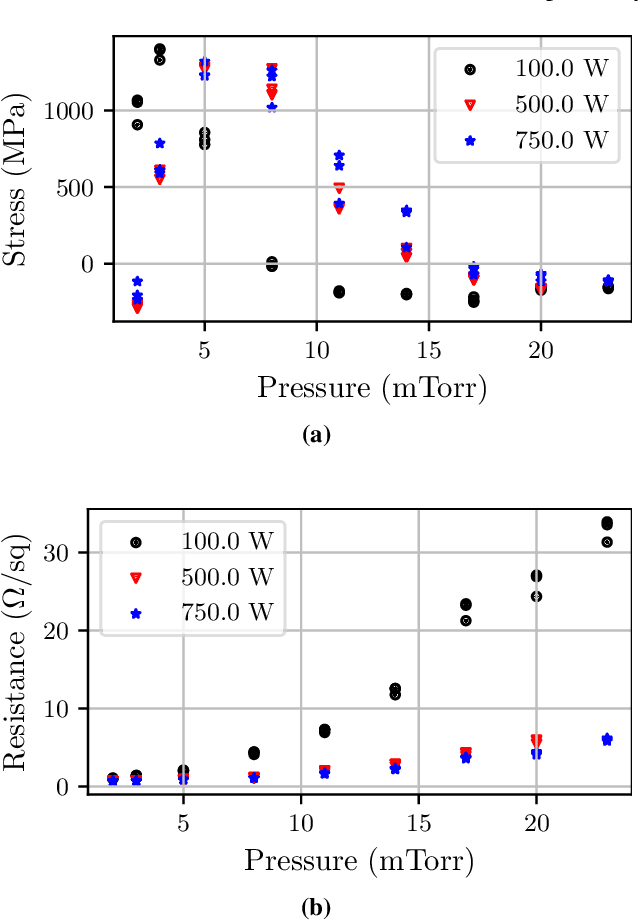
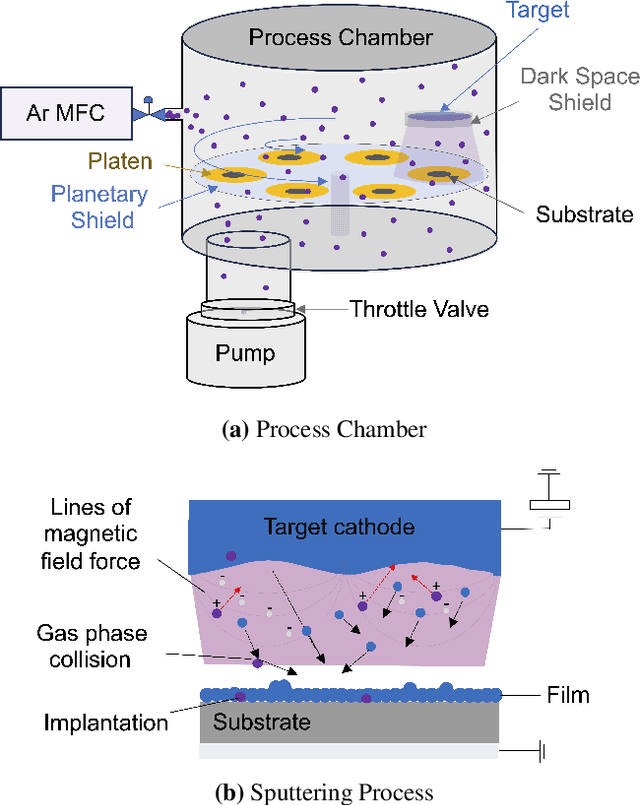
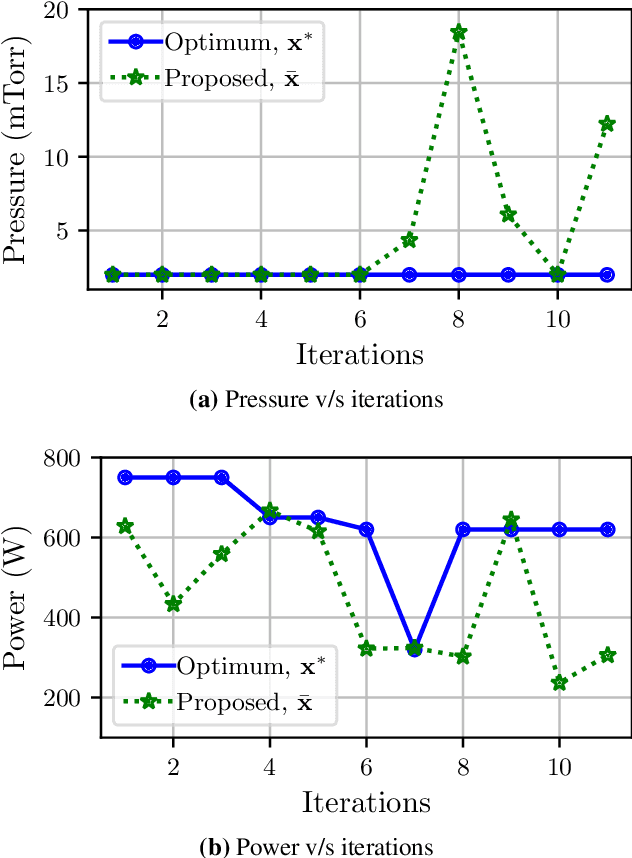
We introduce a Bayesian optimization approach to guide the sputter deposition of molybdenum thin films, aiming to achieve desired residual stress and sheet resistance while minimizing susceptibility to stochastic fluctuations during deposition. Thin films are pivotal in numerous technologies, including semiconductors and optical devices, where their properties are critical. Sputter deposition parameters, such as deposition power, vacuum chamber pressure, and working distance, influence physical properties like residual stress and resistance. Excessive stress and high resistance can impair device performance, necessitating the selection of optimal process parameters. Furthermore, these parameters should ensure the consistency and reliability of thin film properties, assisting in the reproducibility of the devices. However, exploring the multidimensional design space for process optimization is expensive. Bayesian optimization is ideal for optimizing inputs/parameters of general black-box functions without reliance on gradient information. We utilize Bayesian optimization to optimize deposition power and pressure using a custom-built objective function incorporating observed stress and resistance data. Additionally, we integrate prior knowledge of stress variation with pressure into the objective function to prioritize films least affected by stochastic variations. Our findings demonstrate that Bayesian optimization effectively explores the design space and identifies optimal parameter combinations meeting desired stress and resistance specifications.

Spatio-Temporal Super-Resolution of Dynamical Systems using Physics-Informed Deep-Learning

This work presents a physics-informed deep learning-based super-resolution framework to enhance the spatio-temporal resolution of the solution of time-dependent partial differential equations (PDE). Prior works on deep learning-based super-resolution models have shown promise in accelerating engineering design by reducing the computational expense of traditional numerical schemes. However, these models heavily rely on the availability of high-resolution (HR) labeled data needed during training. In this work, we propose a physics-informed deep learning-based framework to enhance the spatial and temporal resolution of coarse-scale (both in space and time) PDE solutions without requiring any HR data. The framework consists of two trainable modules independently super-resolving the PDE solution, first in spatial and then in temporal direction. The physics based losses are implemented in a novel way to ensure tight coupling between the spatio-temporally refined outputs at different times and improve framework accuracy. We analyze the capability of the developed framework by investigating its performance on an elastodynamics problem. It is observed that the proposed framework can successfully super-resolve (both in space and time) the low-resolution PDE solutions while satisfying physics-based constraints and yielding high accuracy. Furthermore, the analysis and obtained speed-up show that the proposed framework is well-suited for integration with traditional numerical methods to reduce computational complexity during engineering design.

Towards Frequency-Based Explanation for Robust CNN

Current explanation techniques towards a transparent Convolutional Neural Network (CNN) mainly focuses on building connections between the human-understandable input features with models' prediction, overlooking an alternative representation of the input, the frequency components decomposition. In this work, we present an analysis of the connection between the distribution of frequency components in the input dataset and the reasoning process the model learns from the data. We further provide quantification analysis about the contribution of different frequency components toward the model's prediction. We show that the vulnerability of the model against tiny distortions is a result of the model is relying on the high-frequency features, the target features of the adversarial (black and white-box) attackers, to make the prediction. We further show that if the model develops stronger association between the low-frequency component with true labels, the model is more robust, which is the explanation of why adversarially trained models are more robust against tiny distortions.