A Deep Learning Framework for Solving Hyperbolic Partial Differential Equations: Part I

Physics informed neural networks (PINNs) have emerged as a powerful tool to provide robust and accurate approximations of solutions to partial differential equations (PDEs). However, PINNs face serious difficulties and challenges when trying to approximate PDEs with dominant hyperbolic character. This research focuses on the development of a physics informed deep learning framework to approximate solutions to nonlinear PDEs that can develop shocks or discontinuities without any a-priori knowledge of the solution or the location of the discontinuities. The work takes motivation from finite element method that solves for solution values at nodes in the discretized domain and use these nodal values to obtain a globally defined solution field. Built on the rigorous mathematical foundations of the discontinuous Galerkin method, the framework naturally handles imposition of boundary conditions (Neumann/Dirichlet), entropy conditions, and regularity requirements. Several numerical experiments and validation with analytical solutions demonstrate the accuracy, robustness, and effectiveness of the proposed framework.

CapsFlow: Optical Flow Estimation with Capsule Networks

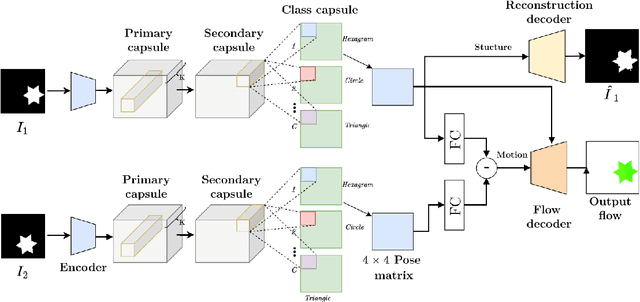
We present a framework to use recently introduced Capsule Networks for solving the problem of Optical Flow, one of the fundamental computer vision tasks. Most of the existing state of the art deep architectures either uses a correlation oepration to match features from them. While correlation layer is sensitive to the choice of hyperparameters and does not put a prior on the underlying structure of the object, spatio temporal features will be limited by the network's receptive field. Also, we as humans look at moving objects as whole, something which cannot be encoded by correlation or spatio temporal features. Capsules, on the other hand, are specialized to model seperate entities and their pose as a continuous matrix. Thus, we show that a simpler linear operation over poses of the objects detected by the capsules in enough to model flow. We show reslts on a small toy dataset where we outperform FlowNetC and PWC-Net models.

Spatio-Temporal Super-Resolution of Dynamical Systems using Physics-Informed Deep-Learning

This work presents a physics-informed deep learning-based super-resolution framework to enhance the spatio-temporal resolution of the solution of time-dependent partial differential equations (PDE). Prior works on deep learning-based super-resolution models have shown promise in accelerating engineering design by reducing the computational expense of traditional numerical schemes. However, these models heavily rely on the availability of high-resolution (HR) labeled data needed during training. In this work, we propose a physics-informed deep learning-based framework to enhance the spatial and temporal resolution of coarse-scale (both in space and time) PDE solutions without requiring any HR data. The framework consists of two trainable modules independently super-resolving the PDE solution, first in spatial and then in temporal direction. The physics based losses are implemented in a novel way to ensure tight coupling between the spatio-temporally refined outputs at different times and improve framework accuracy. We analyze the capability of the developed framework by investigating its performance on an elastodynamics problem. It is observed that the proposed framework can successfully super-resolve (both in space and time) the low-resolution PDE solutions while satisfying physics-based constraints and yielding high accuracy. Furthermore, the analysis and obtained speed-up show that the proposed framework is well-suited for integration with traditional numerical methods to reduce computational complexity during engineering design.

PhySRNet: Physics informed super-resolution network for application in computational solid mechanics

Traditional approaches based on finite element analyses have been successfully used to predict the macro-scale behavior of heterogeneous materials (composites, multicomponent alloys, and polycrystals) widely used in industrial applications. However, this necessitates the mesh size to be smaller than the characteristic length scale of the microstructural heterogeneities in the material leading to computationally expensive and time-consuming calculations. The recent advances in deep learning based image super-resolution (SR) algorithms open up a promising avenue to tackle this computational challenge by enabling researchers to enhance the spatio-temporal resolution of data obtained from coarse mesh simulations. However, technical challenges still remain in developing a high-fidelity SR model for application to computational solid mechanics, especially for materials undergoing large deformation. This work aims at developing a physics-informed deep learning based super-resolution framework (PhySRNet) which enables reconstruction of high-resolution deformation fields (displacement and stress) from their low-resolution counterparts without requiring high-resolution labeled data. We design a synthetic case study to illustrate the effectiveness of the proposed framework and demonstrate that the super-resolved fields match the accuracy of an advanced numerical solver running at 400 times the coarse mesh resolution while simultaneously satisfying the (highly nonlinear) governing laws. The approach opens the door to applying machine learning and traditional numerical approaches in tandem to reduce computational complexity accelerate scientific discovery and engineering design.

Physics-informed neural networks for modeling rate- and temperature-dependent plasticity

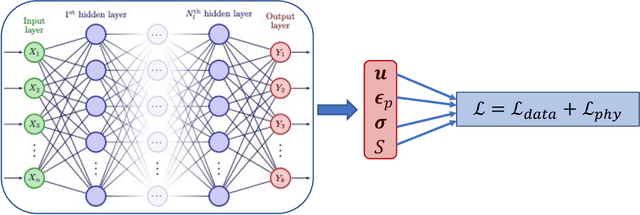
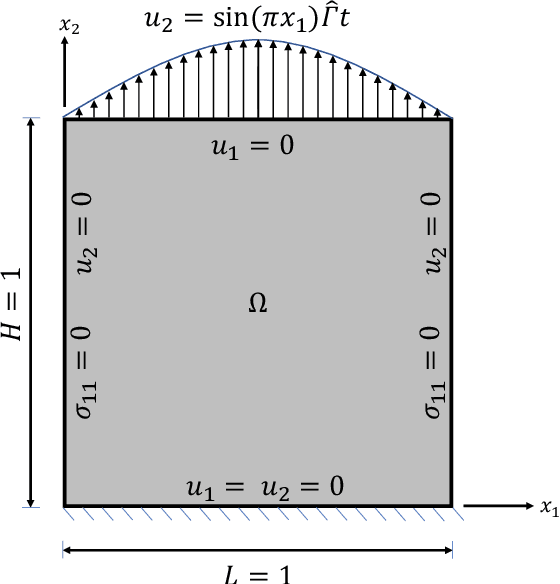
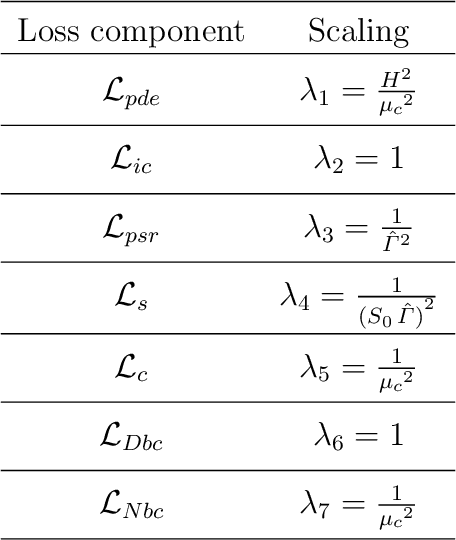
This work presents a physics-informed neural network based framework to model the strain-rate and temperature dependence of the deformation fields (displacement, stress, plastic strain) in elastic-viscoplastic solids. A detailed discussion on the construction of the physics-based loss criterion along with a brief outline on ways to avoid unbalanced back-propagated gradients during training is also presented. We also present a simple strategy with no added computational complexity for choosing scalar weights that balance the interplay between different terms in the composite loss. Moreover, we also highlight a fundamental challenge involving selection of appropriate model outputs so that the mechanical problem can be faithfully solved using neural networks. Finally, the effectiveness of the proposed framework is demonstrated by studying two test problems modeling the elastic-viscoplastic deformation in solids at different strain-rates and temperatures, respectively.

Machine Learning-Accelerated Computational Solid Mechanics: Application to Linear Elasticity

This work presents a novel physics-informed deep learning based super-resolution framework to reconstruct high-resolution deformation fields from low-resolution counterparts, obtained from coarse mesh simulations or experiments. We leverage the governing equations and boundary conditions of the physical system to train the model without using any high-resolution labeled data. The proposed approach is applied to obtain the super-resolved deformation fields from the low-resolution stress and displacement fields obtained by running simulations on a coarse mesh for a body undergoing linear elastic deformation. We demonstrate that the super-resolved fields match the accuracy of an advanced numerical solver running at 400 times the coarse mesh resolution, while simultaneously satisfying the governing laws. A brief evaluation study comparing the performance of two deep learning based super-resolution architectures is also presented.