Physics-informed neural networks for modeling rate- and temperature-dependent plasticity

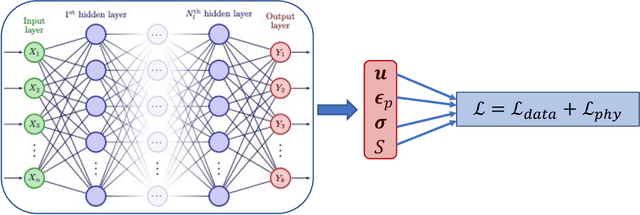
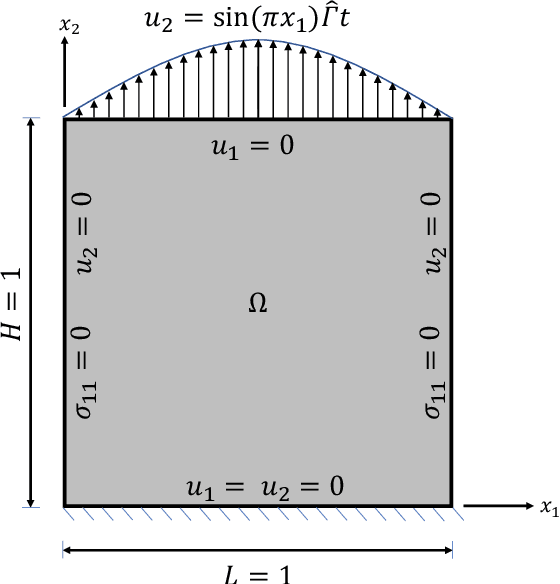
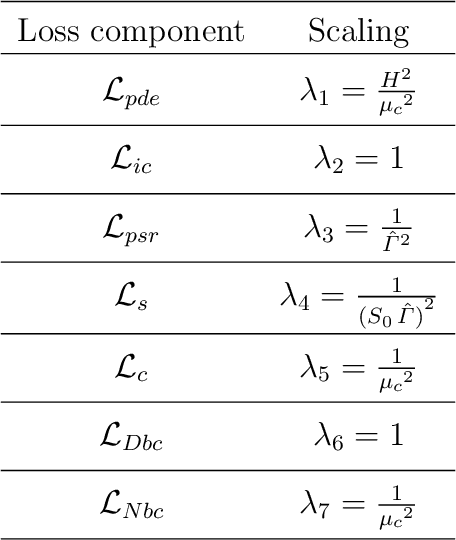
This work presents a physics-informed neural network based framework to model the strain-rate and temperature dependence of the deformation fields (displacement, stress, plastic strain) in elastic-viscoplastic solids. A detailed discussion on the construction of the physics-based loss criterion along with a brief outline on ways to avoid unbalanced back-propagated gradients during training is also presented. We also present a simple strategy with no added computational complexity for choosing scalar weights that balance the interplay between different terms in the composite loss. Moreover, we also highlight a fundamental challenge involving selection of appropriate model outputs so that the mechanical problem can be faithfully solved using neural networks. Finally, the effectiveness of the proposed framework is demonstrated by studying two test problems modeling the elastic-viscoplastic deformation in solids at different strain-rates and temperatures, respectively.

Frequency-compensated PINNs for Fluid-dynamic Design Problems

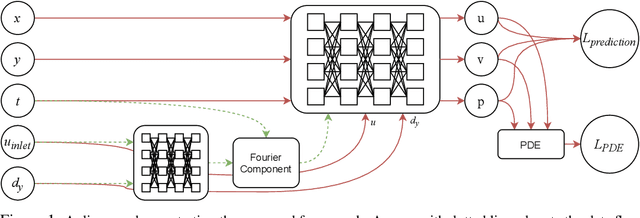
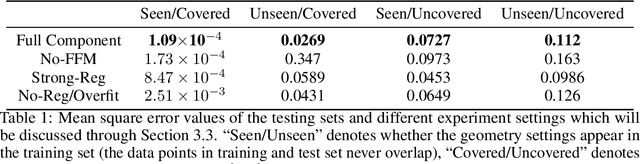
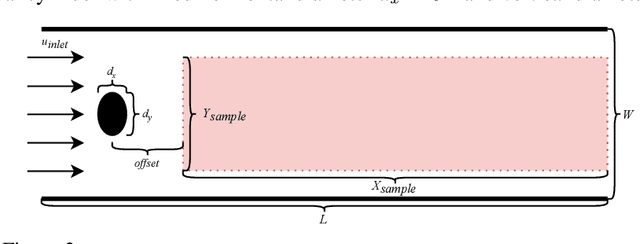
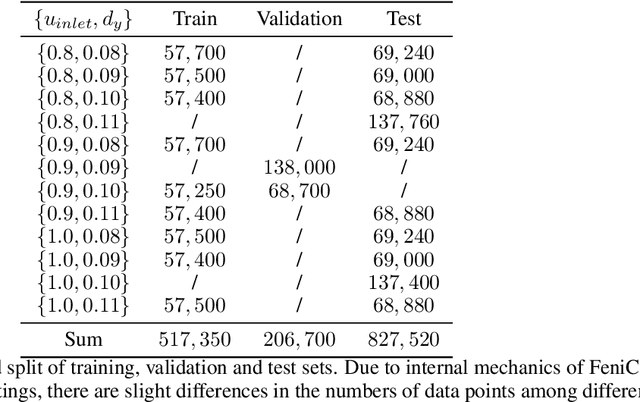
Incompressible fluid flow around a cylinder is one of the classical problems in fluid-dynamics with strong relevance with many real-world engineering problems, for example, design of offshore structures or design of a pin-fin heat exchanger. Thus learning a high-accuracy surrogate for this problem can demonstrate the efficacy of a novel machine learning approach. In this work, we propose a physics-informed neural network (PINN) architecture for learning the relationship between simulation output and the underlying geometry and boundary conditions. In addition to using a physics-based regularization term, the proposed approach also exploits the underlying physics to learn a set of Fourier features, i.e. frequency and phase offset parameters, and then use them for predicting flow velocity and pressure over the spatio-temporal domain. We demonstrate this approach by predicting simulation results over out of range time interval and for novel design conditions. Our results show that incorporation of Fourier features improves the generalization performance over both temporal domain and design space.