Using Parametric PINNs for Predicting Internal and External Turbulent Flows

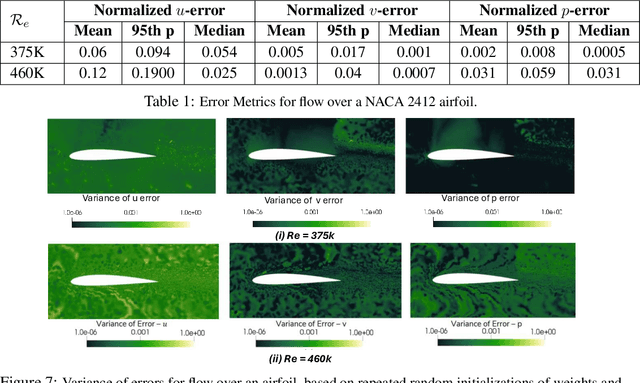
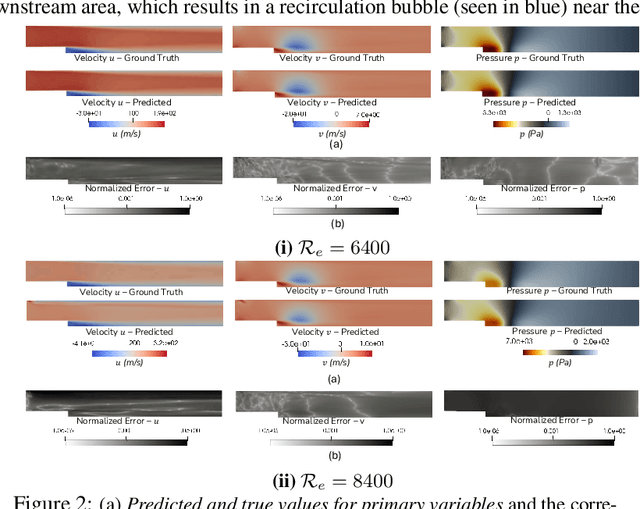
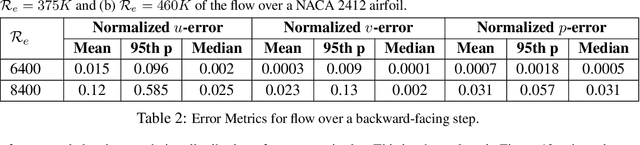
Computational fluid dynamics (CFD) solvers employing two-equation eddy viscosity models are the industry standard for simulating turbulent flows using the Reynolds-averaged Navier-Stokes (RANS) formulation. While these methods are computationally less expensive than direct numerical simulations, they can still incur significant computational costs to achieve the desired accuracy. In this context, physics-informed neural networks (PINNs) offer a promising approach for developing parametric surrogate models that leverage both existing, but limited CFD solutions and the governing differential equations to predict simulation outcomes in a computationally efficient, differentiable, and near real-time manner. In this work, we build upon the previously proposed RANS-PINN framework, which only focused on predicting flow over a cylinder. To investigate the efficacy of RANS-PINN as a viable approach to building parametric surrogate models, we investigate its accuracy in predicting relevant turbulent flow variables for both internal and external flows. To ensure training convergence with a more complex loss function, we adopt a novel sampling approach that exploits the domain geometry to ensure a proper balance among the contributions from various regions within the solution domain. The effectiveness of this framework is then demonstrated for two scenarios that represent a broad class of internal and external flow problems.

An Operator Learning Framework for Spatiotemporal Super-resolution of Scientific Simulations

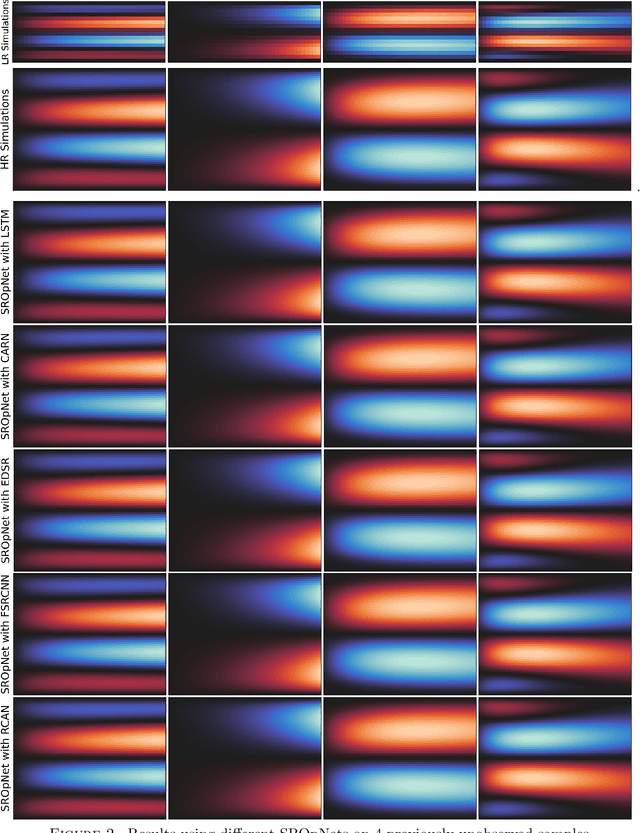
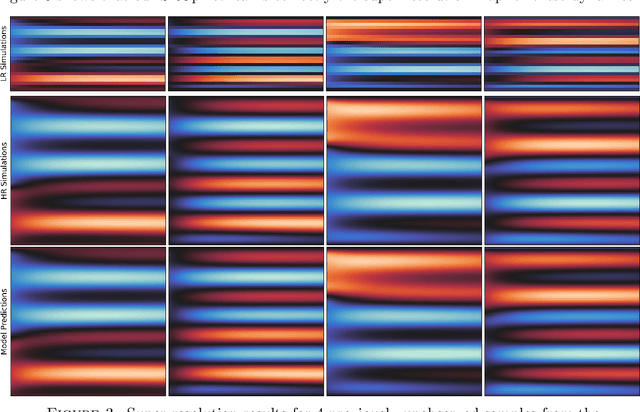
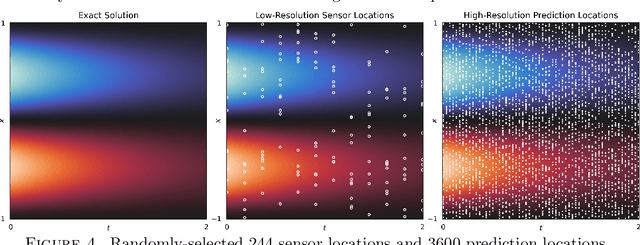
In numerous contexts, high-resolution solutions to partial differential equations are required to capture faithfully essential dynamics which occur at small spatiotemporal scales, but these solutions can be very difficult and slow to obtain using traditional methods due to limited computational resources. A recent direction to circumvent these computational limitations is to use machine learning techniques for super-resolution, to reconstruct high-resolution numerical solutions from low-resolution simulations which can be obtained more efficiently. The proposed approach, the Super Resolution Operator Network (SROpNet), frames super-resolution as an operator learning problem and draws inspiration from existing architectures to learn continuous representations of solutions to parametric differential equations from low-resolution approximations, which can then be evaluated at any desired location. In addition, no restrictions are imposed on the locations of (the fixed number of) spatiotemporal sensors at which the low-resolution approximations are provided, thereby enabling the consideration of a broader spectrum of problems arising in practice, for which many existing super-resolution approaches are not well-suited.

RANS-PINN based Simulation Surrogates for Predicting Turbulent Flows

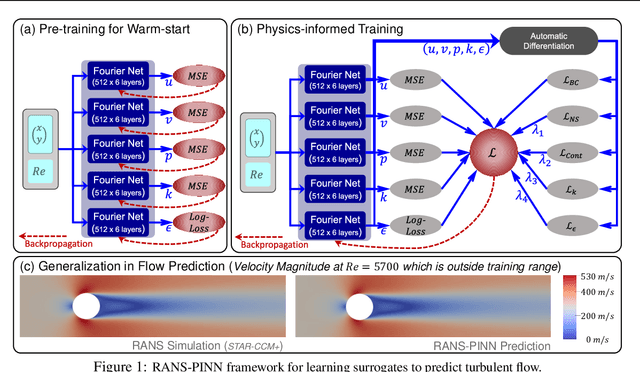
Physics-informed neural networks (PINNs) provide a framework to build surrogate models for dynamical systems governed by differential equations. During the learning process, PINNs incorporate a physics-based regularization term within the loss function to enhance generalization performance. Since simulating dynamics controlled by partial differential equations (PDEs) can be computationally expensive, PINNs have gained popularity in learning parametric surrogates for fluid flow problems governed by Navier-Stokes equations. In this work, we introduce RANS-PINN, a modified PINN framework, to predict flow fields (i.e., velocity and pressure) in high Reynolds number turbulent flow regime. To account for the additional complexity introduced by turbulence, RANS-PINN employs a 2-equation eddy viscosity model based on a Reynolds-averaged Navier-Stokes (RANS) formulation. Furthermore, we adopt a novel training approach that ensures effective initialization and balance among the various components of the loss function. The effectiveness of RANS-PINN framework is then demonstrated using a parametric PINN.

A Neural ODE Interpretation of Transformer Layers

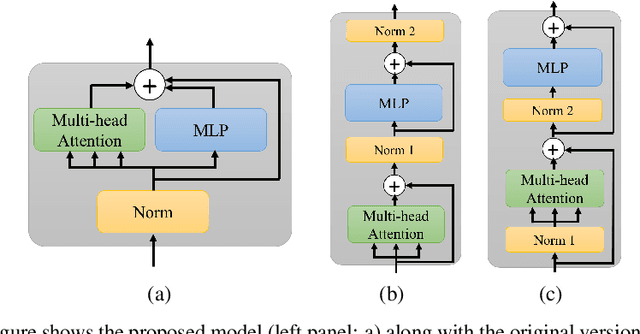
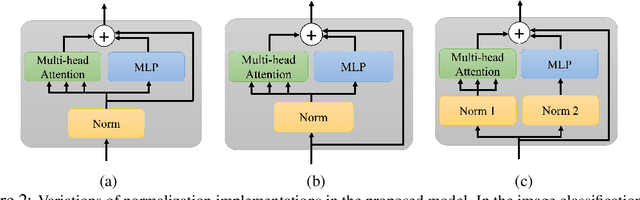
Transformer layers, which use an alternating pattern of multi-head attention and multi-layer perceptron (MLP) layers, provide an effective tool for a variety of machine learning problems. As the transformer layers use residual connections to avoid the problem of vanishing gradients, they can be viewed as the numerical integration of a differential equation. In this extended abstract, we build upon this connection and propose a modification of the internal architecture of a transformer layer. The proposed model places the multi-head attention sublayer and the MLP sublayer parallel to each other. Our experiments show that this simple modification improves the performance of transformer networks in multiple tasks. Moreover, for the image classification task, we show that using neural ODE solvers with a sophisticated integration scheme further improves performance.

Demystifying the Data Need of ML-surrogates for CFD Simulations

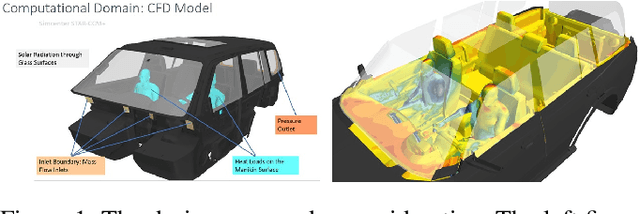
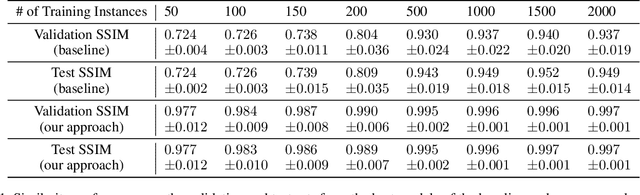
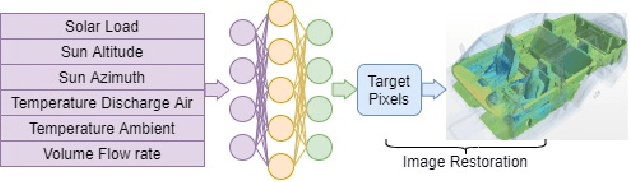
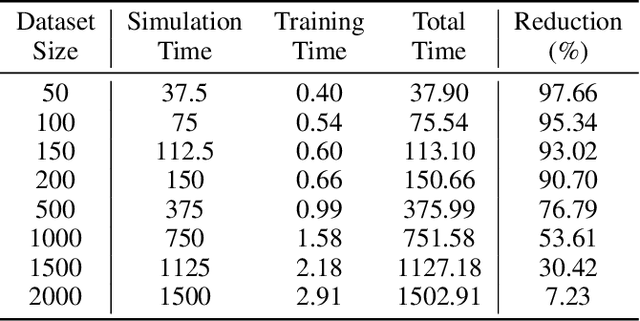
Computational fluid dynamics (CFD) simulations, a critical tool in various engineering applications, often require significant time and compute power to predict flow properties. The high computational cost associated with CFD simulations significantly restricts the scope of design space exploration and limits their use in planning and operational control. To address this issue, machine learning (ML) based surrogate models have been proposed as a computationally efficient tool to accelerate CFD simulations. However, a lack of clarity about CFD data requirements often challenges the widespread adoption of ML-based surrogates among design engineers and CFD practitioners. In this work, we propose an ML-based surrogate model to predict the temperature distribution inside the cabin of a passenger vehicle under various operating conditions and use it to demonstrate the trade-off between prediction performance and training dataset size. Our results show that the prediction accuracy is high and stable even when the training size is gradually reduced from 2000 to 200. The ML-based surrogates also reduce the compute time from ~30 minutes to around ~9 milliseconds. Moreover, even when only 50 CFD simulations are used for training, the temperature trend (e.g., locations of hot/cold regions) predicted by the ML-surrogate matches quite well with the results from CFD simulations.

Physics-informed neural networks for modeling rate- and temperature-dependent plasticity

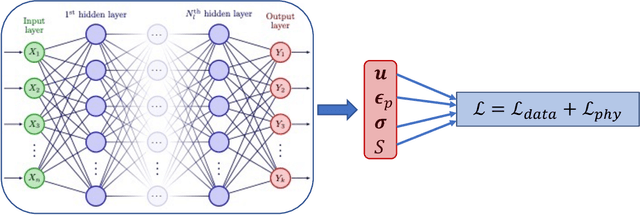
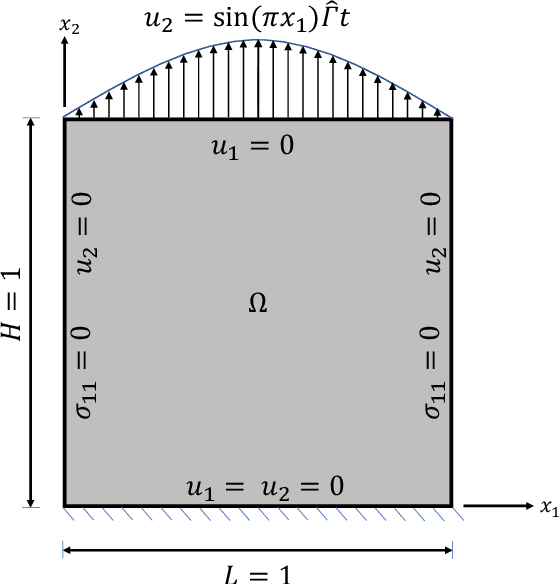
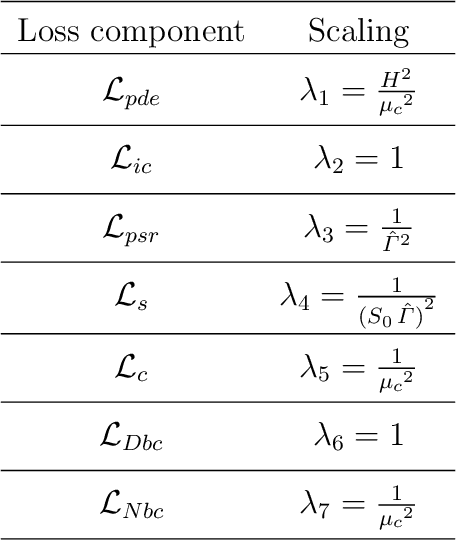
This work presents a physics-informed neural network based framework to model the strain-rate and temperature dependence of the deformation fields (displacement, stress, plastic strain) in elastic-viscoplastic solids. A detailed discussion on the construction of the physics-based loss criterion along with a brief outline on ways to avoid unbalanced back-propagated gradients during training is also presented. We also present a simple strategy with no added computational complexity for choosing scalar weights that balance the interplay between different terms in the composite loss. Moreover, we also highlight a fundamental challenge involving selection of appropriate model outputs so that the mechanical problem can be faithfully solved using neural networks. Finally, the effectiveness of the proposed framework is demonstrated by studying two test problems modeling the elastic-viscoplastic deformation in solids at different strain-rates and temperatures, respectively.

A Decentralized Reinforcement Learning Framework for Efficient Passage of Emergency Vehicles

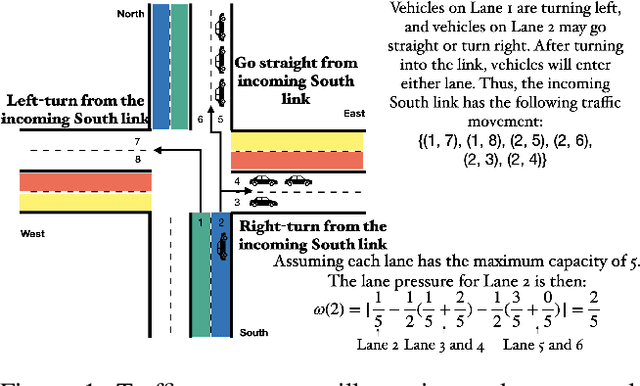
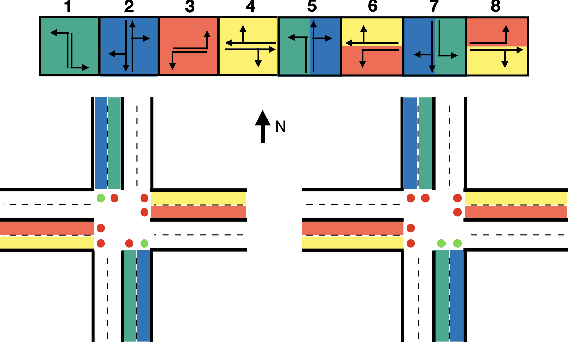
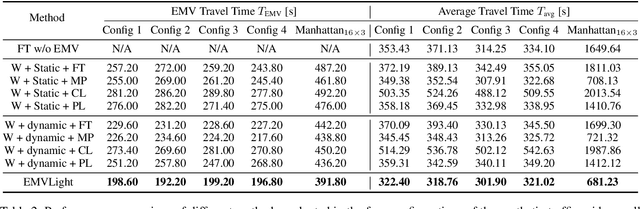
Emergency vehicles (EMVs) play a critical role in a city's response to time-critical events such as medical emergencies and fire outbreaks. The existing approaches to reduce EMV travel time employ route optimization and traffic signal pre-emption without accounting for the coupling between route these two subproblems. As a result, the planned route often becomes suboptimal. In addition, these approaches also do not focus on minimizing disruption to the overall traffic flow. To address these issues, we introduce EMVLight in this paper. This is a decentralized reinforcement learning (RL) framework for simultaneous dynamic routing and traffic signal control. EMVLight extends Dijkstra's algorithm to efficiently update the optimal route for an EMV in real-time as it travels through the traffic network. Consequently, the decentralized RL agents learn network-level cooperative traffic signal phase strategies that reduce EMV travel time and the average travel time of non-EMVs in the network. We have carried out comprehensive experiments with synthetic and real-world maps to demonstrate this benefit. Our results show that EMVLight outperforms benchmark transportation engineering techniques as well as existing RL-based traffic signal control methods.

EMVLight: A Decentralized Reinforcement Learning Framework for Efficient Passage of Emergency Vehicles

Emergency vehicles (EMVs) play a crucial role in responding to time-critical events such as medical emergencies and fire outbreaks in an urban area. The less time EMVs spend traveling through the traffic, the more likely it would help save people's lives and reduce property loss. To reduce the travel time of EMVs, prior work has used route optimization based on historical traffic-flow data and traffic signal pre-emption based on the optimal route. However, traffic signal pre-emption dynamically changes the traffic flow which, in turn, modifies the optimal route of an EMV. In addition, traffic signal pre-emption practices usually lead to significant disturbances in traffic flow and subsequently increase the travel time for non-EMVs. In this paper, we propose EMVLight, a decentralized reinforcement learning (RL) framework for simultaneous dynamic routing and traffic signal control. EMVLight extends Dijkstra's algorithm to efficiently update the optimal route for the EMVs in real time as it travels through the traffic network. The decentralized RL agents learn network-level cooperative traffic signal phase strategies that not only reduce EMV travel time but also reduce the average travel time of non-EMVs in the network. This benefit has been demonstrated through comprehensive experiments with synthetic and real-world maps. These experiments show that EMVLight outperforms benchmark transportation engineering techniques and existing RL-based signal control methods.

A Differentiable Contact Model to Extend Lagrangian and Hamiltonian Neural Networks for Modeling Hybrid Dynamics

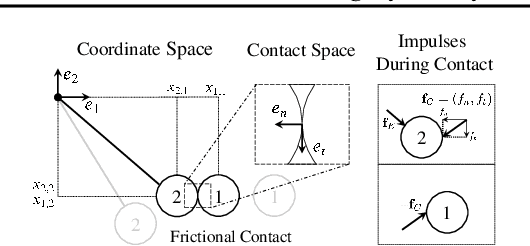
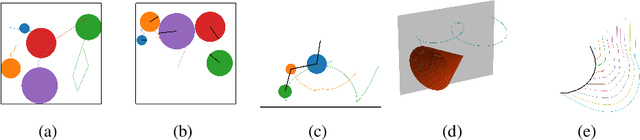
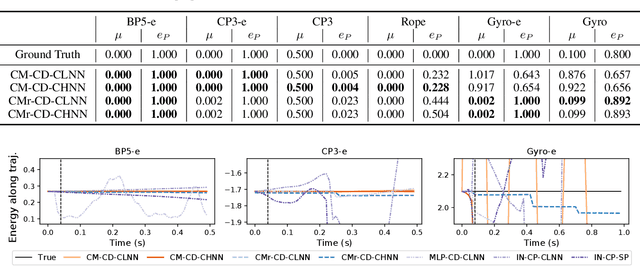
The incorporation of appropriate inductive bias plays a critical role in learning dynamics from data. A growing body of work has been exploring ways to enforce energy conservation in the learned dynamics by incorporating Lagrangian or Hamiltonian dynamics into the design of the neural network architecture. However, these existing approaches are based on differential equations, which does not allow discontinuity in the states, and thereby limits the class of systems one can learn. Real systems, such as legged robots and robotic manipulators, involve contacts and collisions, which introduce discontinuities in the states. In this paper, we introduce a differentiable contact model, which can capture contact mechanics, both frictionless and frictional, as well as both elastic and inelastic. This model can also accommodate inequality constraints, such as limits on the joint angles. The proposed contact model extends the scope of Lagrangian and Hamiltonian neural networks by allowing simultaneous learning of contact properties and system properties. We demonstrate this framework on a series of challenging 2D and 3D physical systems with different coefficients of restitution and friction.

Benchmarking Energy-Conserving Neural Networks for Learning Dynamics from Data

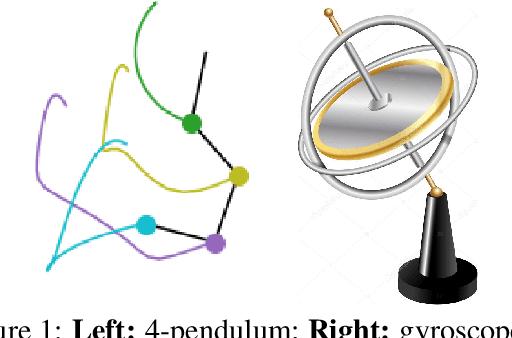
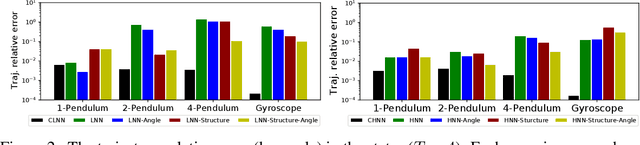
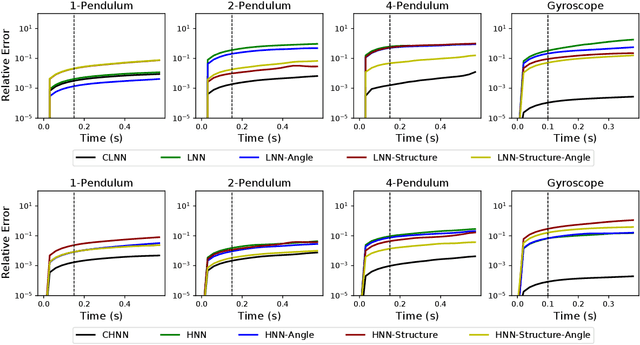
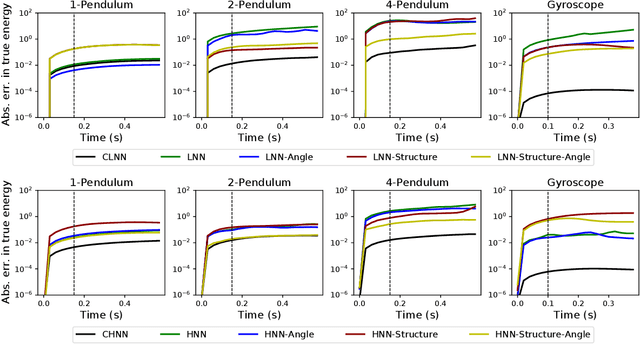
The last few years have witnessed an increased interest in incorporating physics-informed inductive bias in deep learning frameworks. In particular, a growing volume of literature has been exploring ways to enforce energy conservation while using neural networks for learning dynamics from observed time-series data. In this work, we present a comparative analysis of the energy-conserving neural networks - for example, deep Lagrangian network, Hamiltonian neural network, etc. - wherein the underlying physics is encoded in their computation graph. We focus on ten neural network models and explain the similarities and differences between the models. We compare their performance in 4 different physical systems. Our result highlights that using a high-dimensional coordinate system and then imposing restrictions via explicit constraints can lead to higher accuracy in the learned dynamics. We also point out the possibility of leveraging some of these energy-conserving models to design energy-based controllers.