RANS-PINN based Simulation Surrogates for Predicting Turbulent Flows
Paper and Code
Jun 22, 2023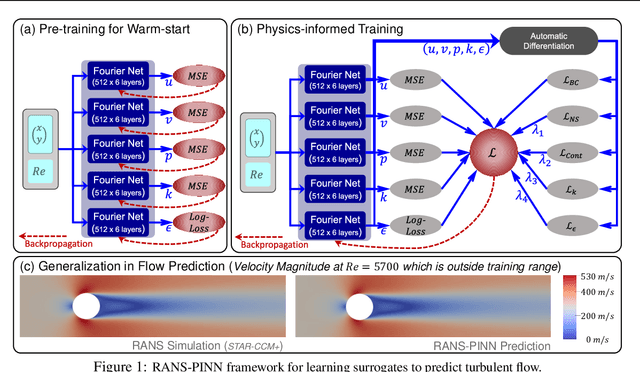



Physics-informed neural networks (PINNs) provide a framework to build surrogate models for dynamical systems governed by differential equations. During the learning process, PINNs incorporate a physics-based regularization term within the loss function to enhance generalization performance. Since simulating dynamics controlled by partial differential equations (PDEs) can be computationally expensive, PINNs have gained popularity in learning parametric surrogates for fluid flow problems governed by Navier-Stokes equations. In this work, we introduce RANS-PINN, a modified PINN framework, to predict flow fields (i.e., velocity and pressure) in high Reynolds number turbulent flow regime. To account for the additional complexity introduced by turbulence, RANS-PINN employs a 2-equation eddy viscosity model based on a Reynolds-averaged Navier-Stokes (RANS) formulation. Furthermore, we adopt a novel training approach that ensures effective initialization and balance among the various components of the loss function. The effectiveness of RANS-PINN framework is then demonstrated using a parametric PINN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge