Geometry-aware PINNs for Turbulent Flow Prediction

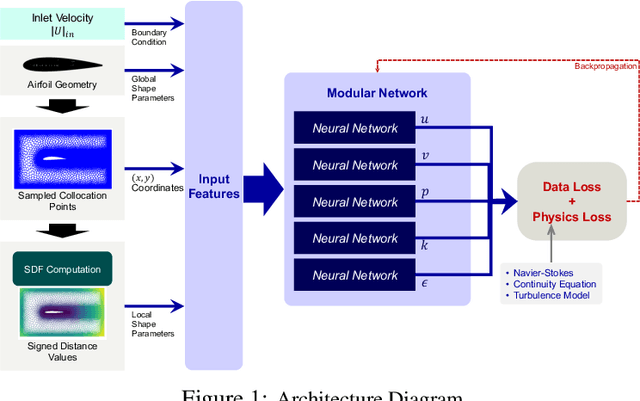
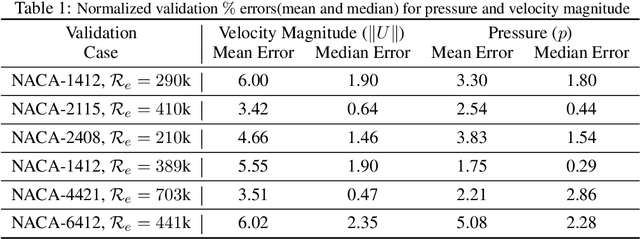
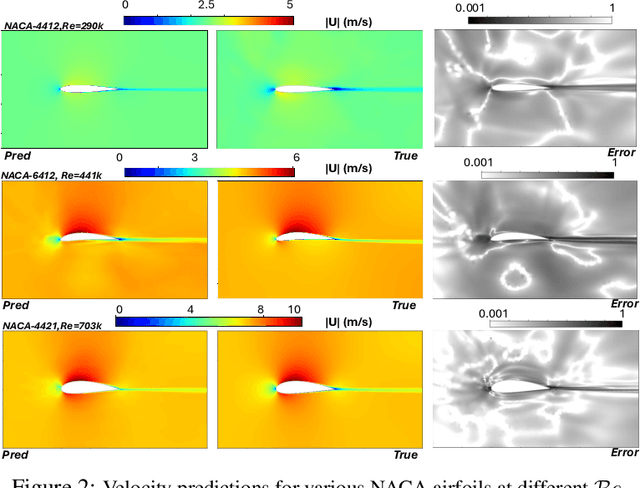
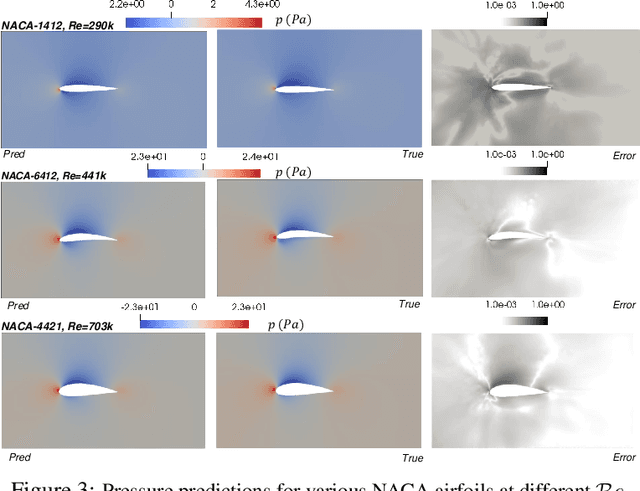
Design exploration or optimization using computational fluid dynamics (CFD) is commonly used in the industry. Geometric variation is a key component of such design problems, especially in turbulent flow scenarios, which involves running costly simulations at every design iteration. While parametric RANS-PINN type approaches have been proven to make effective turbulent surrogates, as a means of predicting unknown Reynolds number flows for a given geometry at near real-time, geometry aware physics informed surrogates with the ability to predict varying geometries are a relatively less studied topic. A novel geometry aware parametric PINN surrogate model has been created, which can predict flow fields for NACA 4 digit airfoils in turbulent conditions, for unseen shapes as well as inlet flow conditions. A local+global approach for embedding has been proposed, where known global design parameters for an airfoil as well as local SDF values can be used as inputs to the model along with velocity inlet/Reynolds number ($\mathcal{R}_e$) to predict the flow fields. A RANS formulation of the Navier-Stokes equations with a 2-equation k-epsilon turbulence model has been used for the PDE losses, in addition to limited CFD data from 8 different NACA airfoils for training. The models have then been validated with unknown NACA airfoils at unseen Reynolds numbers.

Using Parametric PINNs for Predicting Internal and External Turbulent Flows

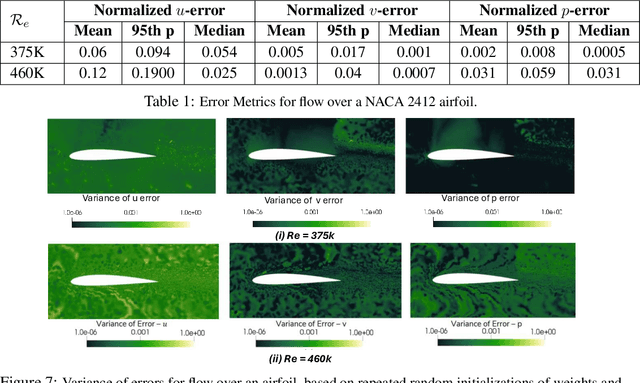
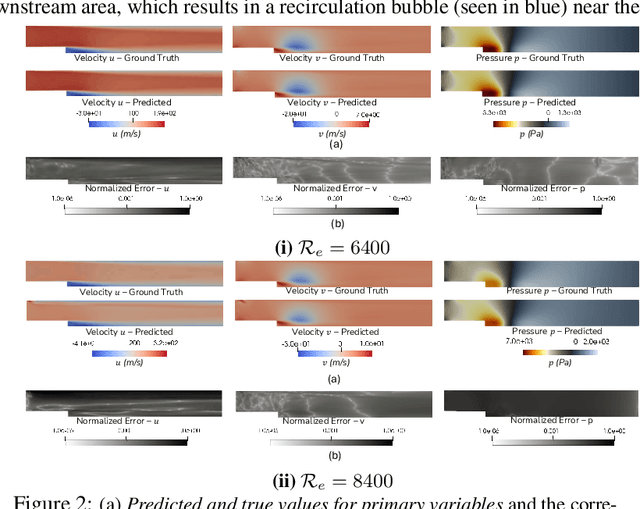
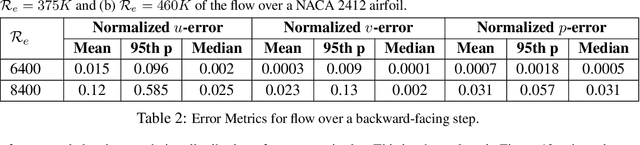
Computational fluid dynamics (CFD) solvers employing two-equation eddy viscosity models are the industry standard for simulating turbulent flows using the Reynolds-averaged Navier-Stokes (RANS) formulation. While these methods are computationally less expensive than direct numerical simulations, they can still incur significant computational costs to achieve the desired accuracy. In this context, physics-informed neural networks (PINNs) offer a promising approach for developing parametric surrogate models that leverage both existing, but limited CFD solutions and the governing differential equations to predict simulation outcomes in a computationally efficient, differentiable, and near real-time manner. In this work, we build upon the previously proposed RANS-PINN framework, which only focused on predicting flow over a cylinder. To investigate the efficacy of RANS-PINN as a viable approach to building parametric surrogate models, we investigate its accuracy in predicting relevant turbulent flow variables for both internal and external flows. To ensure training convergence with a more complex loss function, we adopt a novel sampling approach that exploits the domain geometry to ensure a proper balance among the contributions from various regions within the solution domain. The effectiveness of this framework is then demonstrated for two scenarios that represent a broad class of internal and external flow problems.

RANS-PINN based Simulation Surrogates for Predicting Turbulent Flows

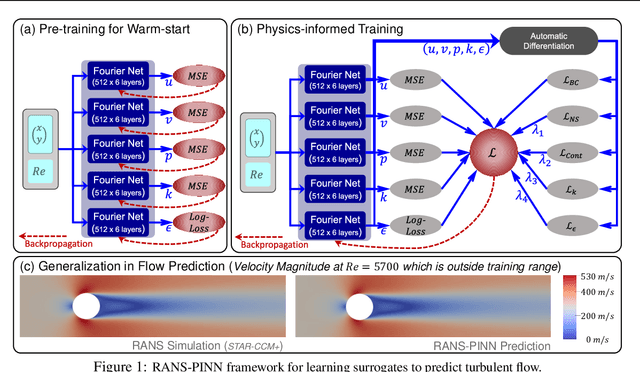
Physics-informed neural networks (PINNs) provide a framework to build surrogate models for dynamical systems governed by differential equations. During the learning process, PINNs incorporate a physics-based regularization term within the loss function to enhance generalization performance. Since simulating dynamics controlled by partial differential equations (PDEs) can be computationally expensive, PINNs have gained popularity in learning parametric surrogates for fluid flow problems governed by Navier-Stokes equations. In this work, we introduce RANS-PINN, a modified PINN framework, to predict flow fields (i.e., velocity and pressure) in high Reynolds number turbulent flow regime. To account for the additional complexity introduced by turbulence, RANS-PINN employs a 2-equation eddy viscosity model based on a Reynolds-averaged Navier-Stokes (RANS) formulation. Furthermore, we adopt a novel training approach that ensures effective initialization and balance among the various components of the loss function. The effectiveness of RANS-PINN framework is then demonstrated using a parametric PINN.

Improving Gradient Computation for Differentiable Physics Simulation with Contacts

Differentiable simulation enables gradients to be back-propagated through physics simulations. In this way, one can learn the dynamics and properties of a physics system by gradient-based optimization or embed the whole differentiable simulation as a layer in a deep learning model for downstream tasks, such as planning and control. However, differentiable simulation at its current stage is not perfect and might provide wrong gradients that deteriorate its performance in learning tasks. In this paper, we study differentiable rigid-body simulation with contacts. We find that existing differentiable simulation methods provide inaccurate gradients when the contact normal direction is not fixed - a general situation when the contacts are between two moving objects. We propose to improve gradient computation by continuous collision detection and leverage the time-of-impact (TOI) to calculate the post-collision velocities. We demonstrate our proposed method, referred to as TOI-Velocity, on two optimal control problems. We show that with TOI-Velocity, we are able to learn an optimal control sequence that matches the analytical solution, while without TOI-Velocity, existing differentiable simulation methods fail to do so.

Differentiable Physics Simulations with Contacts: Do They Have Correct Gradients w.r.t. Position, Velocity and Control?

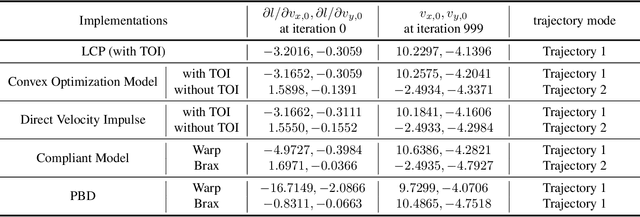
In recent years, an increasing amount of work has focused on differentiable physics simulation and has produced a set of open source projects such as Tiny Differentiable Simulator, Nimble Physics, diffTaichi, Brax, Warp, Dojo and DiffCoSim. By making physics simulations end-to-end differentiable, we can perform gradient-based optimization and learning tasks. A majority of differentiable simulators consider collisions and contacts between objects, but they use different contact models for differentiability. In this paper, we overview four kinds of differentiable contact formulations - linear complementarity problems (LCP), convex optimization models, compliant models and position-based dynamics (PBD). We analyze and compare the gradients calculated by these models and show that the gradients are not always correct. We also demonstrate their ability to learn an optimal control strategy by comparing the learned strategies with the optimal strategy in an analytical form. The codebase to reproduce the experiment results is available at https://github.com/DesmondZhong/diff_sim_grads.