Improving Gradient Computation for Differentiable Physics Simulation with Contacts

Differentiable simulation enables gradients to be back-propagated through physics simulations. In this way, one can learn the dynamics and properties of a physics system by gradient-based optimization or embed the whole differentiable simulation as a layer in a deep learning model for downstream tasks, such as planning and control. However, differentiable simulation at its current stage is not perfect and might provide wrong gradients that deteriorate its performance in learning tasks. In this paper, we study differentiable rigid-body simulation with contacts. We find that existing differentiable simulation methods provide inaccurate gradients when the contact normal direction is not fixed - a general situation when the contacts are between two moving objects. We propose to improve gradient computation by continuous collision detection and leverage the time-of-impact (TOI) to calculate the post-collision velocities. We demonstrate our proposed method, referred to as TOI-Velocity, on two optimal control problems. We show that with TOI-Velocity, we are able to learn an optimal control sequence that matches the analytical solution, while without TOI-Velocity, existing differentiable simulation methods fail to do so.

A Neural ODE Interpretation of Transformer Layers

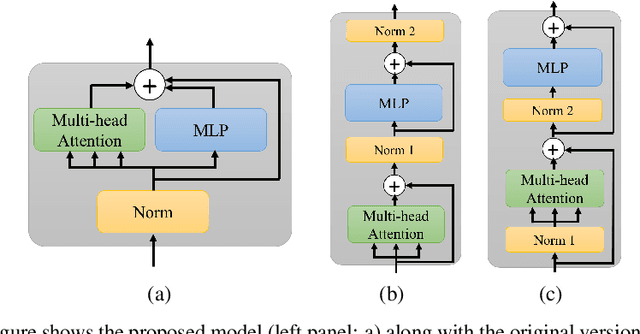
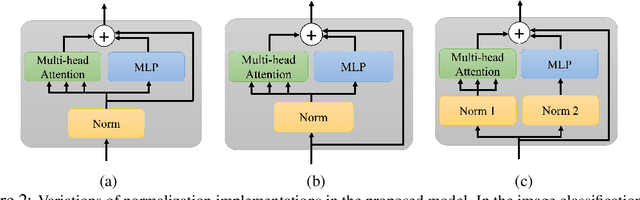
Transformer layers, which use an alternating pattern of multi-head attention and multi-layer perceptron (MLP) layers, provide an effective tool for a variety of machine learning problems. As the transformer layers use residual connections to avoid the problem of vanishing gradients, they can be viewed as the numerical integration of a differential equation. In this extended abstract, we build upon this connection and propose a modification of the internal architecture of a transformer layer. The proposed model places the multi-head attention sublayer and the MLP sublayer parallel to each other. Our experiments show that this simple modification improves the performance of transformer networks in multiple tasks. Moreover, for the image classification task, we show that using neural ODE solvers with a sophisticated integration scheme further improves performance.

Differentiable Physics Simulations with Contacts: Do They Have Correct Gradients w.r.t. Position, Velocity and Control?

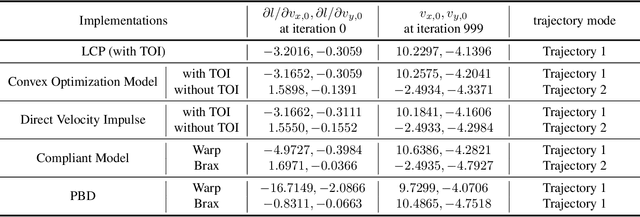
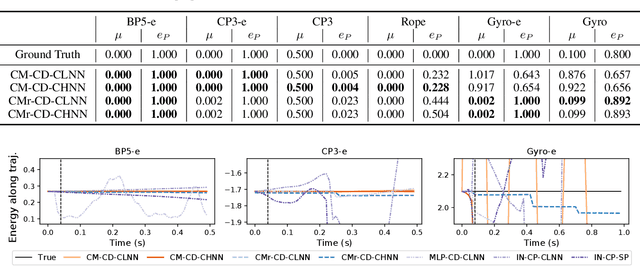
In recent years, an increasing amount of work has focused on differentiable physics simulation and has produced a set of open source projects such as Tiny Differentiable Simulator, Nimble Physics, diffTaichi, Brax, Warp, Dojo and DiffCoSim. By making physics simulations end-to-end differentiable, we can perform gradient-based optimization and learning tasks. A majority of differentiable simulators consider collisions and contacts between objects, but they use different contact models for differentiability. In this paper, we overview four kinds of differentiable contact formulations - linear complementarity problems (LCP), convex optimization models, compliant models and position-based dynamics (PBD). We analyze and compare the gradients calculated by these models and show that the gradients are not always correct. We also demonstrate their ability to learn an optimal control strategy by comparing the learned strategies with the optimal strategy in an analytical form. The codebase to reproduce the experiment results is available at https://github.com/DesmondZhong/diff_sim_grads.

A Decentralized Reinforcement Learning Framework for Efficient Passage of Emergency Vehicles

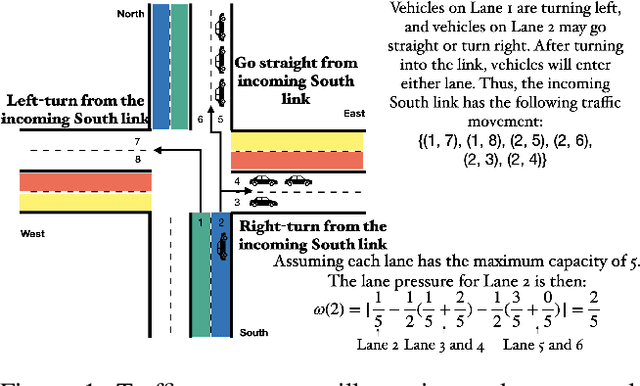
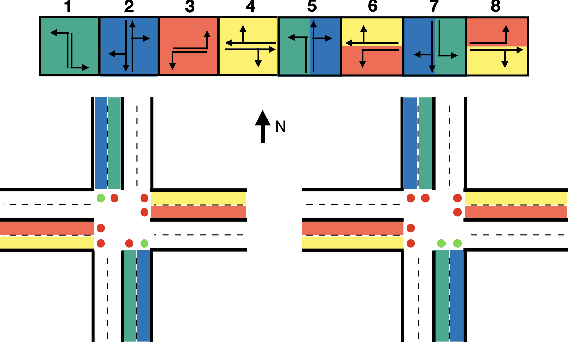
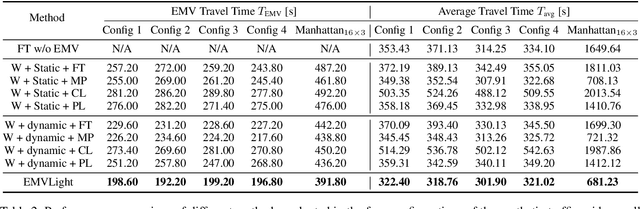
Emergency vehicles (EMVs) play a critical role in a city's response to time-critical events such as medical emergencies and fire outbreaks. The existing approaches to reduce EMV travel time employ route optimization and traffic signal pre-emption without accounting for the coupling between route these two subproblems. As a result, the planned route often becomes suboptimal. In addition, these approaches also do not focus on minimizing disruption to the overall traffic flow. To address these issues, we introduce EMVLight in this paper. This is a decentralized reinforcement learning (RL) framework for simultaneous dynamic routing and traffic signal control. EMVLight extends Dijkstra's algorithm to efficiently update the optimal route for an EMV in real-time as it travels through the traffic network. Consequently, the decentralized RL agents learn network-level cooperative traffic signal phase strategies that reduce EMV travel time and the average travel time of non-EMVs in the network. We have carried out comprehensive experiments with synthetic and real-world maps to demonstrate this benefit. Our results show that EMVLight outperforms benchmark transportation engineering techniques as well as existing RL-based traffic signal control methods.

EMVLight: A Decentralized Reinforcement Learning Framework for Efficient Passage of Emergency Vehicles

Emergency vehicles (EMVs) play a crucial role in responding to time-critical events such as medical emergencies and fire outbreaks in an urban area. The less time EMVs spend traveling through the traffic, the more likely it would help save people's lives and reduce property loss. To reduce the travel time of EMVs, prior work has used route optimization based on historical traffic-flow data and traffic signal pre-emption based on the optimal route. However, traffic signal pre-emption dynamically changes the traffic flow which, in turn, modifies the optimal route of an EMV. In addition, traffic signal pre-emption practices usually lead to significant disturbances in traffic flow and subsequently increase the travel time for non-EMVs. In this paper, we propose EMVLight, a decentralized reinforcement learning (RL) framework for simultaneous dynamic routing and traffic signal control. EMVLight extends Dijkstra's algorithm to efficiently update the optimal route for the EMVs in real time as it travels through the traffic network. The decentralized RL agents learn network-level cooperative traffic signal phase strategies that not only reduce EMV travel time but also reduce the average travel time of non-EMVs in the network. This benefit has been demonstrated through comprehensive experiments with synthetic and real-world maps. These experiments show that EMVLight outperforms benchmark transportation engineering techniques and existing RL-based signal control methods.

A Differentiable Contact Model to Extend Lagrangian and Hamiltonian Neural Networks for Modeling Hybrid Dynamics

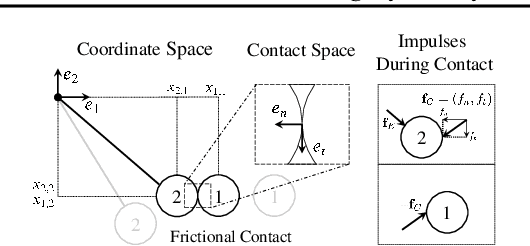
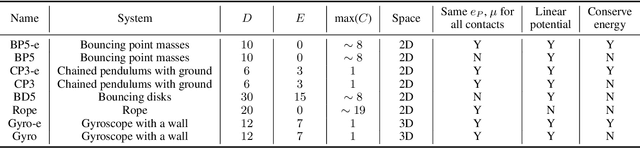
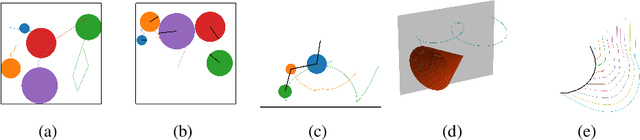
The incorporation of appropriate inductive bias plays a critical role in learning dynamics from data. A growing body of work has been exploring ways to enforce energy conservation in the learned dynamics by incorporating Lagrangian or Hamiltonian dynamics into the design of the neural network architecture. However, these existing approaches are based on differential equations, which does not allow discontinuity in the states, and thereby limits the class of systems one can learn. Real systems, such as legged robots and robotic manipulators, involve contacts and collisions, which introduce discontinuities in the states. In this paper, we introduce a differentiable contact model, which can capture contact mechanics, both frictionless and frictional, as well as both elastic and inelastic. This model can also accommodate inequality constraints, such as limits on the joint angles. The proposed contact model extends the scope of Lagrangian and Hamiltonian neural networks by allowing simultaneous learning of contact properties and system properties. We demonstrate this framework on a series of challenging 2D and 3D physical systems with different coefficients of restitution and friction.

Benchmarking Energy-Conserving Neural Networks for Learning Dynamics from Data

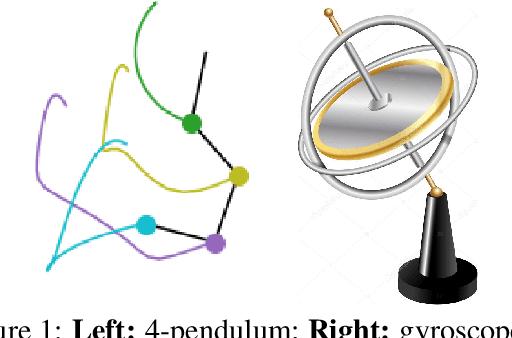
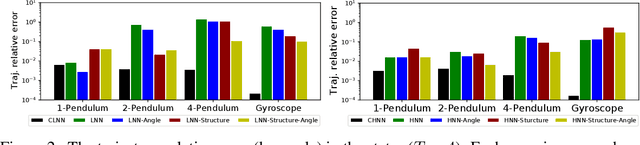
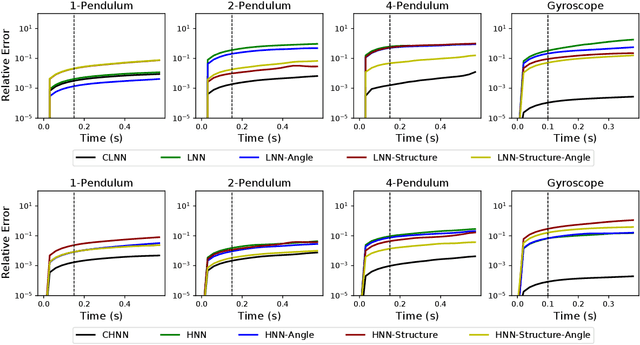
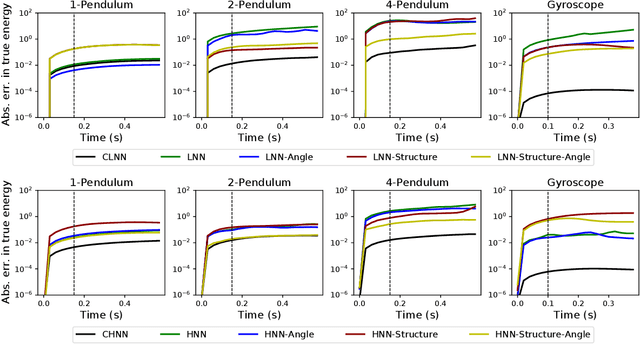
The last few years have witnessed an increased interest in incorporating physics-informed inductive bias in deep learning frameworks. In particular, a growing volume of literature has been exploring ways to enforce energy conservation while using neural networks for learning dynamics from observed time-series data. In this work, we present a comparative analysis of the energy-conserving neural networks - for example, deep Lagrangian network, Hamiltonian neural network, etc. - wherein the underlying physics is encoded in their computation graph. We focus on ten neural network models and explain the similarities and differences between the models. We compare their performance in 4 different physical systems. Our result highlights that using a high-dimensional coordinate system and then imposing restrictions via explicit constraints can lead to higher accuracy in the learned dynamics. We also point out the possibility of leveraging some of these energy-conserving models to design energy-based controllers.

Unsupervised Learning of Lagrangian Dynamics from Images for Prediction and Control

Recent approaches for modelling dynamics of physical systems with neural networks enforce Lagrangian or Hamiltonian structure to improve prediction and generalization. However, these approaches fail to handle the case when coordinates are embedded in high-dimensional data such as images. We introduce a new unsupervised neural network model that learns Lagrangian dynamics from images, with interpretability that benefits prediction and control. The model infers Lagrangian dynamics on generalized coordinates that are simultaneously learned with a coordinate-aware variational autoencoder (VAE). The VAE is designed to account for the geometry of physical systems composed of multiple rigid bodies in the plane. By inferring interpretable Lagrangian dynamics, the model learns physical system properties, such as kinetic and potential energy, which enables long-term prediction of dynamics in the image space and synthesis of energy-based controllers.

Dissipative SymODEN: Encoding Hamiltonian Dynamics with Dissipation and Control into Deep Learning

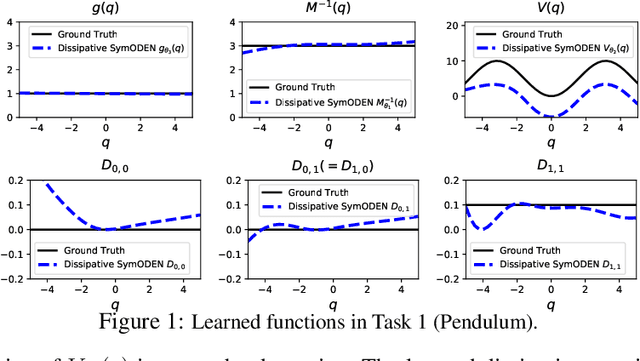
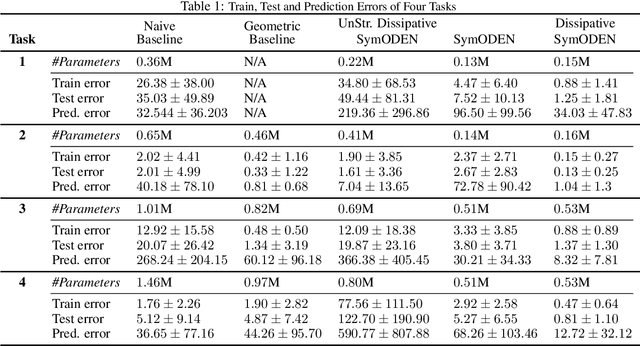
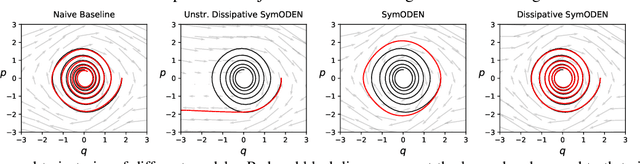
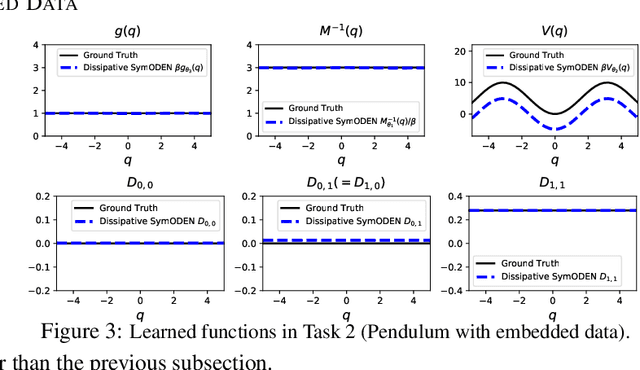
In this work, we introduce Dissipative SymODEN, a deep learning architecture which can infer the dynamics of a physical system with dissipation from observed state trajectories. To improve prediction accuracy while reducing network size, Dissipative SymODEN encodes the port-Hamiltonian dynamics with energy dissipation and external input into the design of its computation graph and learns the dynamics in a structured way. The learned model, by revealing key aspects of the system, such as the inertia, dissipation, and potential energy, paves the way for energy-based controllers.

Symplectic ODE-Net: Learning Hamiltonian Dynamics with Control

In this paper, we introduce Symplectic ODE-Net (SymODEN), a deep learning framework which can infer the dynamics of a physical system from observed state trajectories. To achieve better generalization with fewer training samples, SymODEN incorporates appropriate inductive bias by designing the associated computation graph in a physics-informed manner. In particular, we enforce Hamiltonian dynamics with control to learn the underlying dynamics in a transparent way which can then be leveraged to draw insight about relevant physical aspects of the system, such as mass and potential energy. In addition, we propose a parametrization which can enforce this Hamiltonian formalism even when the generalized coordinate data is embedded in a high-dimensional space or we can only access velocity data instead of generalized momentum. This framework, by offering interpretable, physically-consistent models for physical systems, opens up new possibilities for synthesizing model-based control strategies.