Benchmarking Energy-Conserving Neural Networks for Learning Dynamics from Data
Paper and Code
Dec 30, 2020
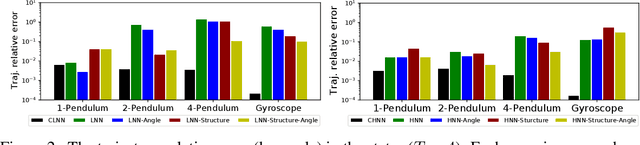
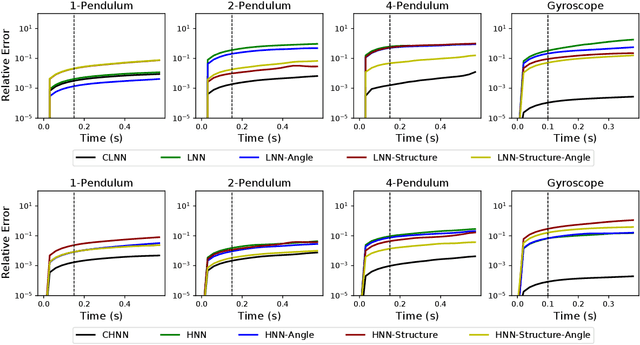
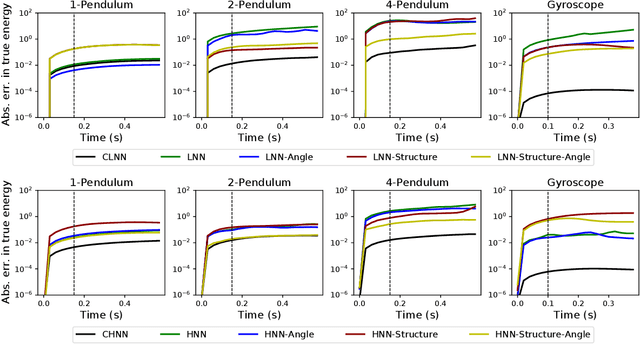
The last few years have witnessed an increased interest in incorporating physics-informed inductive bias in deep learning frameworks. In particular, a growing volume of literature has been exploring ways to enforce energy conservation while using neural networks for learning dynamics from observed time-series data. In this work, we present a comparative analysis of the energy-conserving neural networks - for example, deep Lagrangian network, Hamiltonian neural network, etc. - wherein the underlying physics is encoded in their computation graph. We focus on ten neural network models and explain the similarities and differences between the models. We compare their performance in 4 different physical systems. Our result highlights that using a high-dimensional coordinate system and then imposing restrictions via explicit constraints can lead to higher accuracy in the learned dynamics. We also point out the possibility of leveraging some of these energy-conserving models to design energy-based controllers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge