Physics-informed neural networks for modeling rate- and temperature-dependent plasticity
Paper and Code
Jan 20, 2022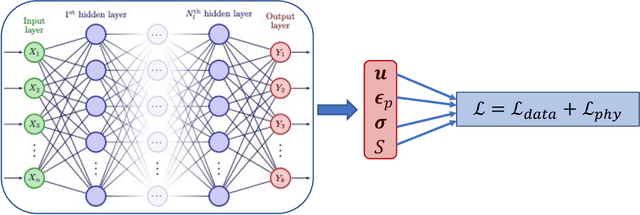

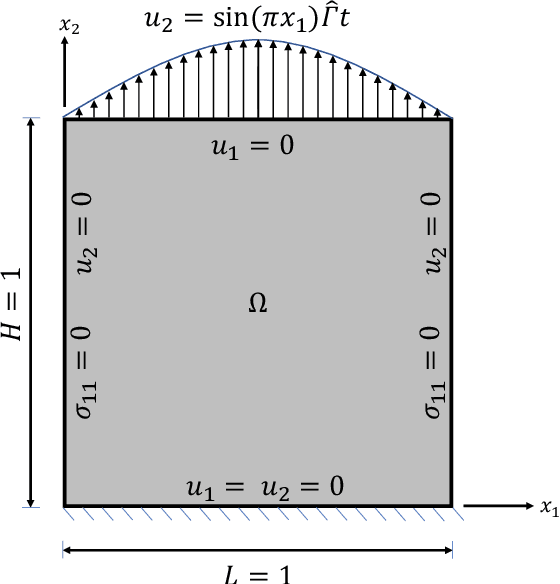
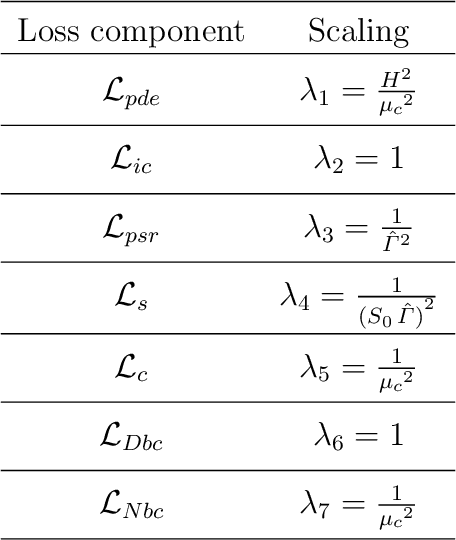
This work presents a physics-informed neural network based framework to model the strain-rate and temperature dependence of the deformation fields (displacement, stress, plastic strain) in elastic-viscoplastic solids. A detailed discussion on the construction of the physics-based loss criterion along with a brief outline on ways to avoid unbalanced back-propagated gradients during training is also presented. We also present a simple strategy with no added computational complexity for choosing scalar weights that balance the interplay between different terms in the composite loss. Moreover, we also highlight a fundamental challenge involving selection of appropriate model outputs so that the mechanical problem can be faithfully solved using neural networks. Finally, the effectiveness of the proposed framework is demonstrated by studying two test problems modeling the elastic-viscoplastic deformation in solids at different strain-rates and temperatures, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge