Bayesian Inverse Problems with Conditional Sinkhorn Generative Adversarial Networks in Least Volume Latent Spaces

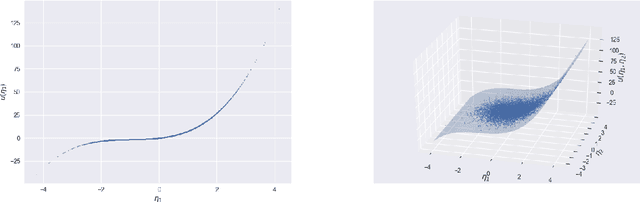
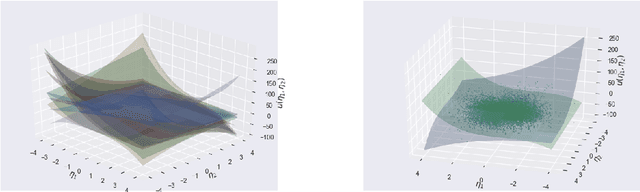
Solving inverse problems in scientific and engineering fields has long been intriguing and holds great potential for many applications, yet most techniques still struggle to address issues such as high dimensionality, nonlinearity and model uncertainty inherent in these problems. Recently, generative models such as Generative Adversarial Networks (GANs) have shown great potential in approximating complex high dimensional conditional distributions and have paved the way for characterizing posterior densities in Bayesian inverse problems, yet the problems' high dimensionality and high nonlinearity often impedes the model's training. In this paper we show how to tackle these issues with Least Volume--a novel unsupervised nonlinear dimension reduction method--that can learn to represent the given datasets with the minimum number of latent variables while estimating their intrinsic dimensions. Once the low dimensional latent spaces are identified, efficient and accurate training of conditional generative models becomes feasible, resulting in a latent conditional GAN framework for posterior inference. We demonstrate the power of the proposed methodology on a variety of applications including inversion of parameters in systems of ODEs and high dimensional hydraulic conductivities in subsurface flow problems, and reveal the impact of the observables' and unobservables' intrinsic dimensions on inverse problems.

Bayesian learning of orthogonal embeddings for multi-fidelity Gaussian Processes

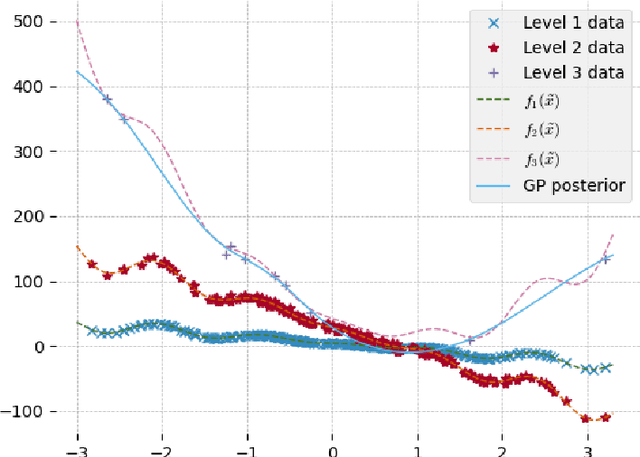
We present a Bayesian approach to identify optimal transformations that map model input points to low dimensional latent variables. The "projection" mapping consists of an orthonormal matrix that is considered a priori unknown and needs to be inferred jointly with the GP parameters, conditioned on the available training data. The proposed Bayesian inference scheme relies on a two-step iterative algorithm that samples from the marginal posteriors of the GP parameters and the projection matrix respectively, both using Markov Chain Monte Carlo (MCMC) sampling. In order to take into account the orthogonality constraints imposed on the orthonormal projection matrix, a Geodesic Monte Carlo sampling algorithm is employed, that is suitable for exploiting probability measures on manifolds. We extend the proposed framework to multi-fidelity models using GPs including the scenarios of training multiple outputs together. We validate our framework on three synthetic problems with a known lower-dimensional subspace. The benefits of our proposed framework, are illustrated on the computationally challenging three-dimensional aerodynamic optimization of a last-stage blade for an industrial gas turbine, where we study the effect of an 85-dimensional airfoil shape parameterization on two output quantities of interest, specifically on the aerodynamic efficiency and the degree of reaction.

Sparse Polynomial Chaos expansions using Variational Relevance Vector Machines

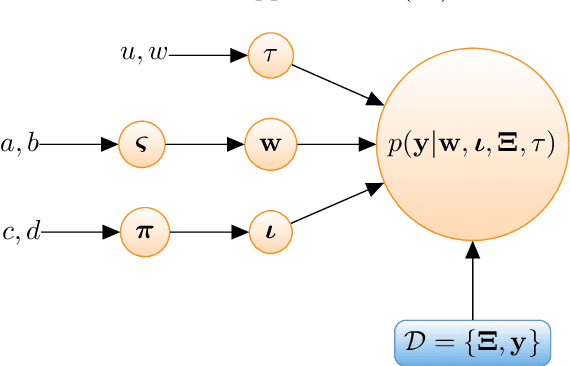
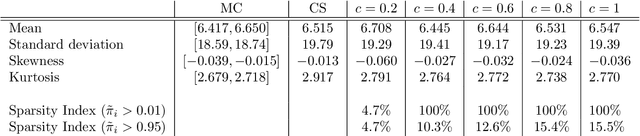
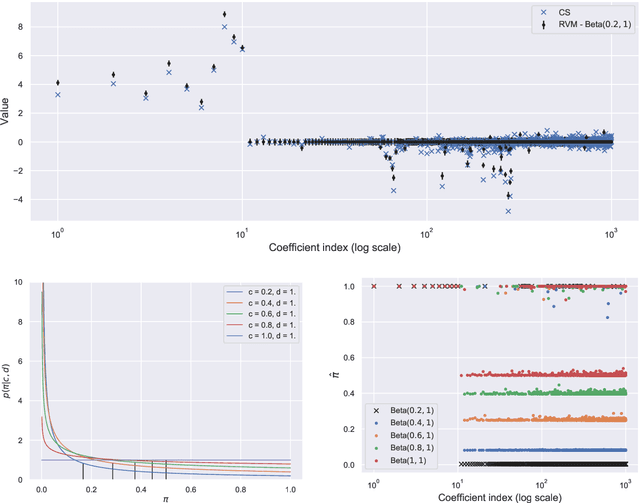
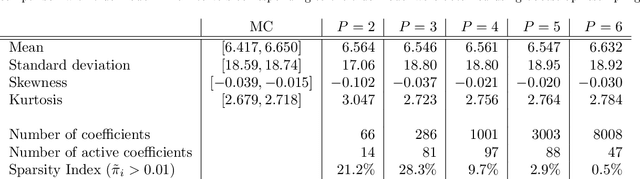
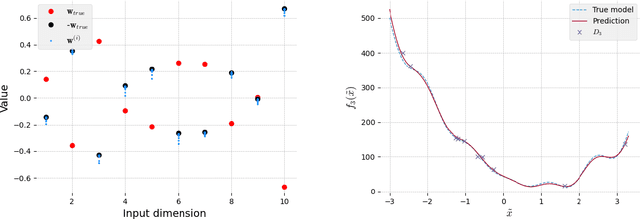
The challenges for non-intrusive methods for Polynomial Chaos modeling lie in the computational efficiency and accuracy under a limited number of model simulations. These challenges can be addressed by enforcing sparsity in the series representation through retaining only the most important basis terms. In this work, we present a novel sparse Bayesian learning technique for obtaining sparse Polynomial Chaos expansions which is based on a Relevance Vector Machine model and is trained using Variational Inference. The methodology shows great potential in high-dimensional data-driven settings using relatively few data points and achieves user-controlled sparse levels that are comparable to other methods such as compressive sensing. The proposed approach is illustrated on two numerical examples, a synthetic response function that is explored for validation purposes and a low-carbon steel plate with random Young's modulus and random loading, which is modeled by stochastic finite element with 38 input random variables.

Compressive sensing adaptation for polynomial chaos expansions

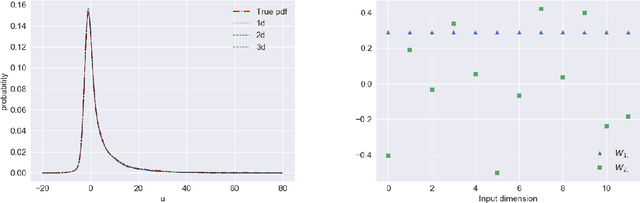
Basis adaptation in Homogeneous Chaos spaces rely on a suitable rotation of the underlying Gaussian germ. Several rotations have been proposed in the literature resulting in adaptations with different convergence properties. In this paper we present a new adaptation mechanism that builds on compressive sensing algorithms, resulting in a reduced polynomial chaos approximation with optimal sparsity. The developed adaptation algorithm consists of a two-step optimization procedure that computes the optimal coefficients and the input projection matrix of a low dimensional chaos expansion with respect to an optimally rotated basis. We demonstrate the attractive features of our algorithm through several numerical examples including the application on Large-Eddy Simulation (LES) calculations of turbulent combustion in a HIFiRE scramjet engine.

Efficient Bayesian experimentation using an expected information gain lower bound

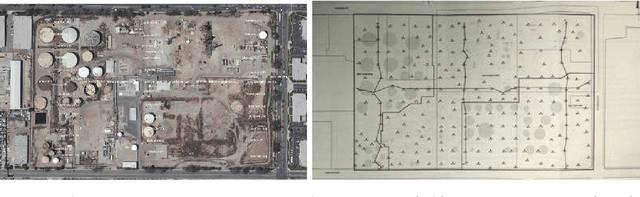
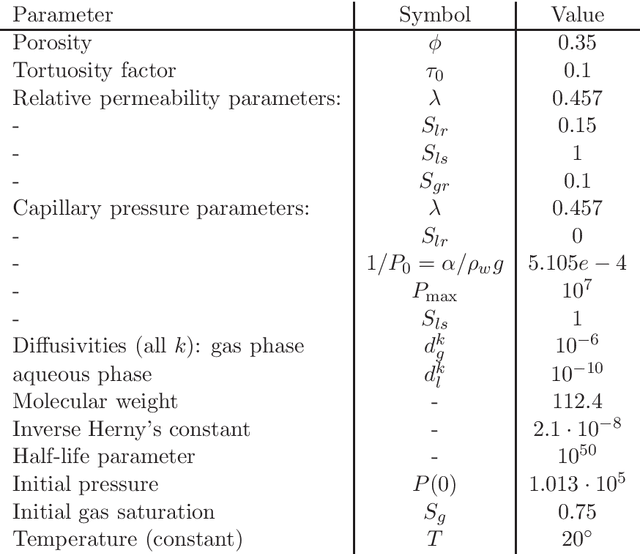
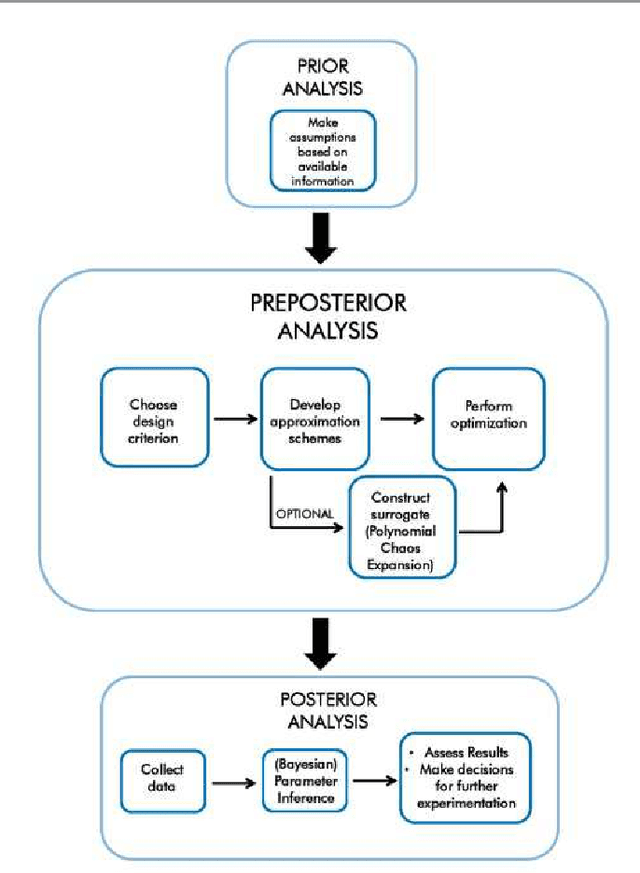
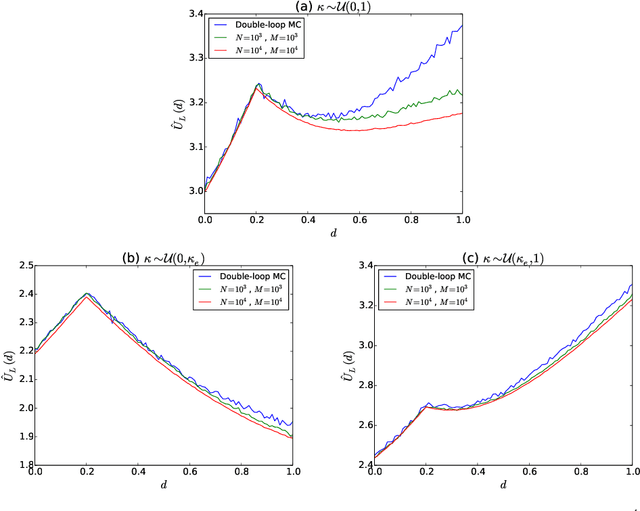
Experimental design is crucial for inference where limitations in the data collection procedure are present due to cost or other restrictions. Optimal experimental designs determine parameters that in some appropriate sense make the data the most informative possible. In a Bayesian setting this is translated to updating to the best possible posterior. Information theoretic arguments have led to the formation of the expected information gain as a design criterion. This can be evaluated mainly by Monte Carlo sampling and maximized by using stochastic approximation methods, both known for being computationally expensive tasks. We propose a framework where a lower bound of the expected information gain is used as an alternative design criterion. In addition to alleviating the computational burden, this also addresses issues concerning estimation bias. The problem of permeability inference in a large contaminated area is used to demonstrate the validity of our approach where we employ the massively parallel version of the multiphase multicomponent simulator TOUGH2 to simulate contaminant transport and a Polynomial Chaos approximation of the forward model that further accelerates the objective function evaluations. The proposed methodology is demonstrated to a setting where field measurements are available.

Variational Reformulation of Bayesian Inverse Problems

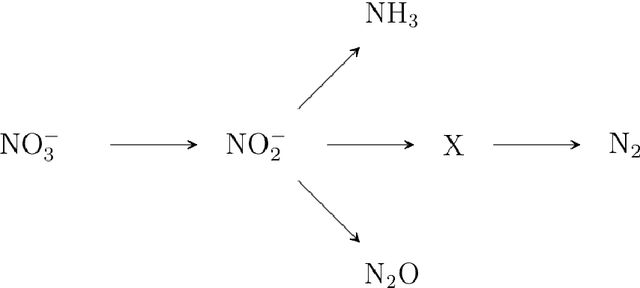
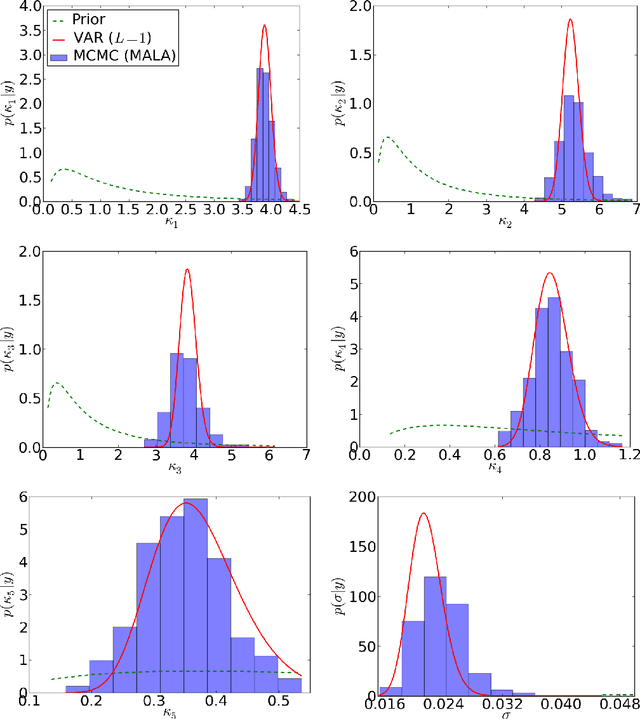
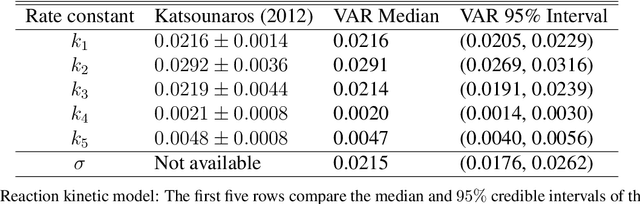
The classical approach to inverse problems is based on the optimization of a misfit function. Despite its computational appeal, such an approach suffers from many shortcomings, e.g., non-uniqueness of solutions, modeling prior knowledge, etc. The Bayesian formalism to inverse problems avoids most of the difficulties encountered by the optimization approach, albeit at an increased computational cost. In this work, we use information theoretic arguments to cast the Bayesian inference problem in terms of an optimization problem. The resulting scheme combines the theoretical soundness of fully Bayesian inference with the computational efficiency of a simple optimization.