Inverse design with conditional cascaded diffusion models

Adjoint-based design optimizations are usually computationally expensive and those costs scale with resolution. To address this, researchers have proposed machine learning approaches for inverse design that can predict higher-resolution solutions from lower cost/resolution ones. Due to the recent success of diffusion models over traditional generative models, we extend the use of diffusion models for multi-resolution tasks by proposing the conditional cascaded diffusion model (cCDM). Compared to GANs, cCDM is more stable to train, and each diffusion model within the cCDM can be trained independently, thus each model's parameters can be tuned separately to maximize the performance of the pipeline. Our study compares cCDM against a cGAN model with transfer learning. Our results demonstrate that the cCDM excels in capturing finer details, preserving volume fraction constraints, and minimizing compliance errors in multi-resolution tasks when a sufficient amount of high-resolution training data (more than 102 designs) is available. Furthermore, we explore the impact of training data size on the performance of both models. While both models show decreased performance with reduced high-resolution training data, the cCDM loses its superiority to the cGAN model with transfer learning when training data is limited (less than 102), and we show the break-even point for this transition. Also, we highlight that while the diffusion model may achieve better pixel-wise performance in both low-resolution and high-resolution scenarios, this does not necessarily guarantee that the model produces optimal compliance error or constraint satisfaction.

Bayesian Inverse Problems with Conditional Sinkhorn Generative Adversarial Networks in Least Volume Latent Spaces

Solving inverse problems in scientific and engineering fields has long been intriguing and holds great potential for many applications, yet most techniques still struggle to address issues such as high dimensionality, nonlinearity and model uncertainty inherent in these problems. Recently, generative models such as Generative Adversarial Networks (GANs) have shown great potential in approximating complex high dimensional conditional distributions and have paved the way for characterizing posterior densities in Bayesian inverse problems, yet the problems' high dimensionality and high nonlinearity often impedes the model's training. In this paper we show how to tackle these issues with Least Volume--a novel unsupervised nonlinear dimension reduction method--that can learn to represent the given datasets with the minimum number of latent variables while estimating their intrinsic dimensions. Once the low dimensional latent spaces are identified, efficient and accurate training of conditional generative models becomes feasible, resulting in a latent conditional GAN framework for posterior inference. We demonstrate the power of the proposed methodology on a variety of applications including inversion of parameters in systems of ODEs and high dimensional hydraulic conductivities in subsurface flow problems, and reveal the impact of the observables' and unobservables' intrinsic dimensions on inverse problems.

Compressing Latent Space via Least Volume

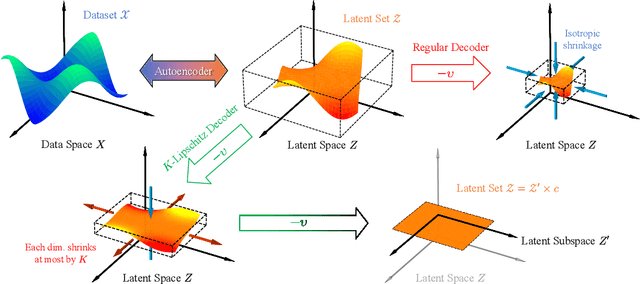
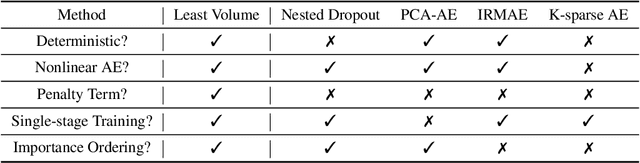
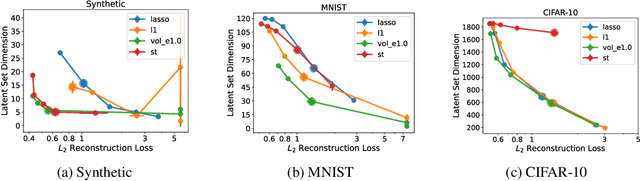
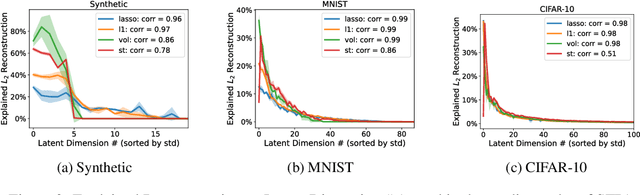
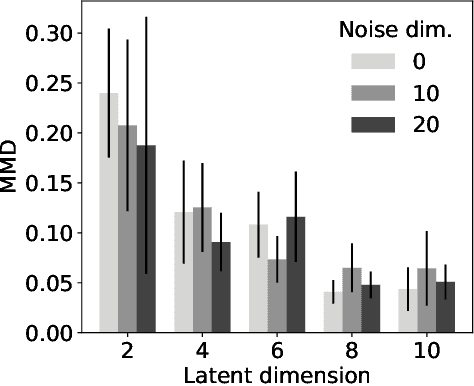
This paper introduces Least Volume-a simple yet effective regularization inspired by geometric intuition-that can reduce the necessary number of latent dimensions needed by an autoencoder without requiring any prior knowledge of the intrinsic dimensionality of the dataset. We show that the Lipschitz continuity of the decoder is the key to making it work, provide a proof that PCA is just a linear special case of it, and reveal that it has a similar PCA-like importance ordering effect when applied to nonlinear models. We demonstrate the intuition behind the regularization on some pedagogical toy problems, and its effectiveness on several benchmark problems, including MNIST, CIFAR-10 and CelebA.

IH-GAN: A Conditional Generative Model for Implicit Surface-Based Inverse Design of Cellular Structures

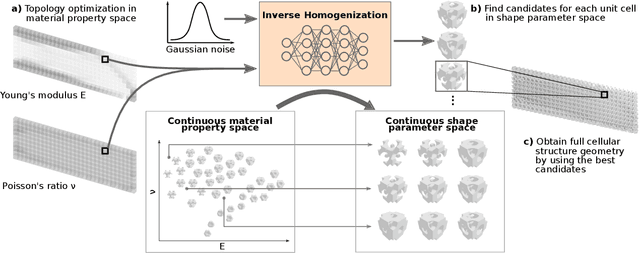
Variable-density cellular structures can overcome connectivity and manufacturability issues of topologically-optimized, functionally graded structures, particularly when those structures are represented as discrete density maps. One na\"ive approach to creating variable-density cellular structures is simply replacing the discrete density map with an unselective type of unit cells having corresponding densities. However, doing so breaks the desired mechanical behavior, as equivalent density alone does not guarantee equivalent mechanical properties. Another approach uses homogenization methods to estimate each pre-defined unit cell's effective properties and remaps the unit cells following a scaling law. However, a scaling law merely mitigates the problem by performing an indirect and inaccurate mapping from the material property space to single-type unit cells. In contrast, we propose a deep generative model that resolves this problem by automatically learning an accurate mapping and generating diverse cellular unit cells conditioned on desired properties (i.e., Young's modulus and Poisson's ratio). We demonstrate our method via the use of implicit function-based unit cells and conditional generative adversarial networks. Results show that our method can 1) generate various unit cells that satisfy given material properties with high accuracy (relative error <5%), 2) create functionally graded cellular structures with high-quality interface connectivity (98.7% average overlap area at interfaces), and 3) improve the structural performance over the conventional topology-optimized variable-density structure (84.4% reduction in concentrated stress and extra 7% reduction in displacement).

Airfoil Design Parameterization and Optimization using Bézier Generative Adversarial Networks

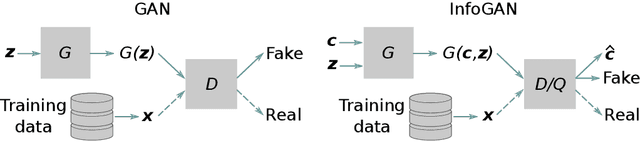
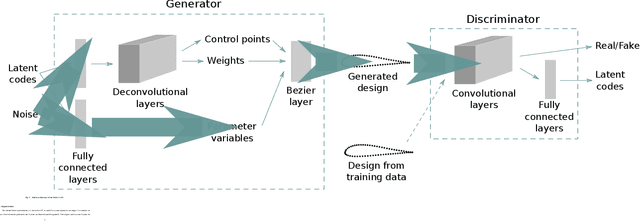
Global optimization of aerodynamic shapes usually requires a large number of expensive computational fluid dynamics simulations because of the high dimensionality of the design space. One approach to combat this problem is to reduce the design space dimension by obtaining a new representation. This requires a parametric function that compactly and sufficiently describes useful variation in shapes. We propose a deep generative model, B\'ezier-GAN, to parameterize aerodynamic designs by learning from shape variations in an existing database. The resulted new parameterization can accelerate design optimization convergence by improving the representation compactness while maintaining sufficient representation capacity. We use the airfoil design as an example to demonstrate the idea and analyze B\'ezier-GAN's representation capacity and compactness. Results show that B\'ezier-GAN both (1) learns smooth and realistic shape representations for a wide range of airfoils and (2) empirically accelerates optimization convergence by at least two times compared to state-of-the-art parameterization methods.

Forming Diverse Teams from Sequentially Arriving People

Collaborative work often benefits from having teams or organizations with heterogeneous members. In this paper, we present a method to form such diverse teams from people arriving sequentially over time. We define a monotone submodular objective function that combines the diversity and quality of a team and propose an algorithm to maximize the objective while satisfying multiple constraints. This allows us to balance both how diverse the team is and how well it can perform the task at hand. Using crowd experiments, we show that, in practice, the algorithm leads to large gains in team diversity. Using simulations, we show how to quantify the additional cost of forming diverse teams and how to address the problem of simultaneously maximizing diversity for several attributes (e.g., country of origin, gender). Our method has applications in collaborative work ranging from team formation, the assignment of workers to teams in crowdsourcing, and reviewer allocation to journal papers arriving sequentially. Our code is publicly accessible for further research.

Adaptive Expansion Bayesian Optimization for Unbounded Global Optimization

Bayesian optimization is normally performed within fixed variable bounds. In cases like hyperparameter tuning for machine learning algorithms, setting the variable bounds is not trivial. It is hard to guarantee that any fixed bounds will include the true global optimum. We propose a Bayesian optimization approach that only needs to specify an initial search space that does not necessarily include the global optimum, and expands the search space when necessary. However, over-exploration may occur during the search space expansion. Our method can adaptively balance exploration and exploitation in an expanding space. Results on a range of synthetic test functions and an MLP hyperparameter optimization task show that the proposed method out-performs or at least as good as the current state-of-the-art methods.

Algorithms for Optimal Diverse Matching

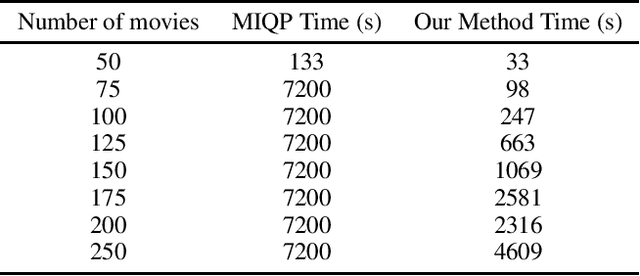
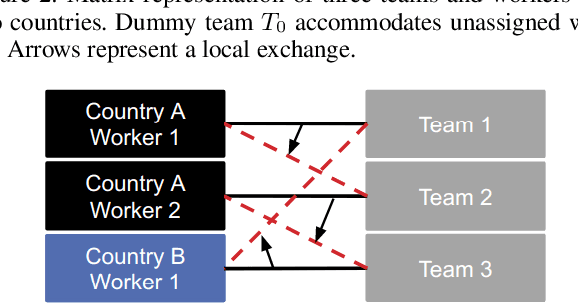
Bipartite b-matching, where agents on one side of a market are matched to one or more agents or items on the other, is a classical model that is used in myriad application areas such as healthcare, advertising, education, and general resource allocation. Traditionally, the primary goal of such models is to maximize a linear function of the constituent matches (e.g., linear social welfare maximization) subject to some constraints. Recent work has studied a new goal of balancing whole-match diversity and economic efficiency, where the objective is instead a monotone submodular function over the matching. These more general models are largely NP-hard. In this work, we develop a combinatorial algorithm that constructs provably-optimal diverse b-matchings in pseudo-polynomial time. Then, we show how to extend our algorithm to solve new variations of the diverse b-matching problem. We then compare directly, on real-world datasets, against the state-of-the-art, quadratic-programming-based approach to solving diverse b-matching problems and show that our method outperforms it in both speed and (anytime) solution quality.

BézierGAN: Automatic Generation of Smooth Curves from Interpretable Low-Dimensional Parameters

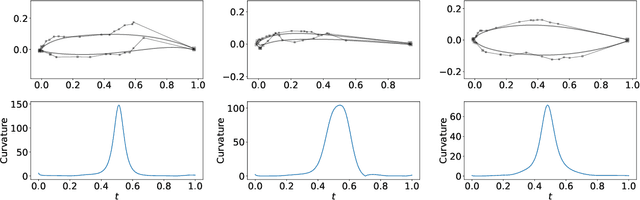
Many real-world objects are designed by smooth curves, especially in the domain of aerospace and ship, where aerodynamic shapes (e.g., airfoils) and hydrodynamic shapes (e.g., hulls) are designed. To facilitate the design process of those objects, we propose a deep learning based generative model that can synthesize smooth curves. The model maps a low-dimensional latent representation to a sequence of discrete points sampled from a rational B\'ezier curve. We demonstrate the performance of our method in completing both synthetic and real-world generative tasks. Results show that our method can generate diverse and realistic curves, while preserving consistent shape variation in the latent space, which is favorable for latent space design optimization or design space exploration.

Active Expansion Sampling for Learning Feasible Domains in an Unbounded Input Space

Many engineering problems require identifying feasible domains under implicit constraints. One example is finding acceptable car body styling designs based on constraints like aesthetics and functionality. Current active-learning based methods learn feasible domains for bounded input spaces. However, we usually lack prior knowledge about how to set those input variable bounds. Bounds that are too small will fail to cover all feasible domains; while bounds that are too large will waste query budget. To avoid this problem, we introduce Active Expansion Sampling (AES), a method that identifies (possibly disconnected) feasible domains over an unbounded input space. AES progressively expands our knowledge of the input space, and uses successive exploitation and exploration stages to switch between learning the decision boundary and searching for new feasible domains. We show that AES has a misclassification loss guarantee within the explored region, independent of the number of iterations or labeled samples. Thus it can be used for real-time prediction of samples' feasibility within the explored region. We evaluate AES on three test examples and compare AES with two adaptive sampling methods -- the Neighborhood-Voronoi algorithm and the straddle heuristic -- that operate over fixed input variable bounds.