Algorithms for Optimal Diverse Matching

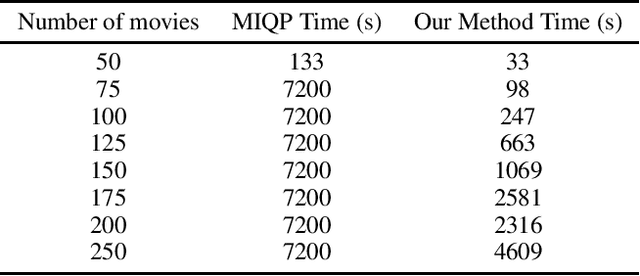
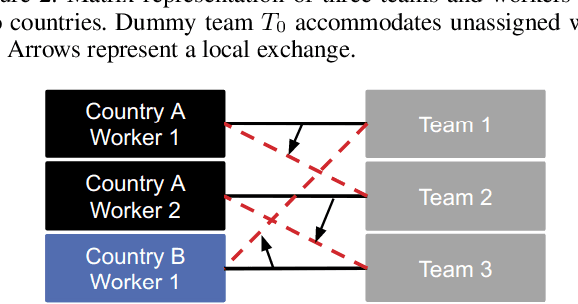
Bipartite b-matching, where agents on one side of a market are matched to one or more agents or items on the other, is a classical model that is used in myriad application areas such as healthcare, advertising, education, and general resource allocation. Traditionally, the primary goal of such models is to maximize a linear function of the constituent matches (e.g., linear social welfare maximization) subject to some constraints. Recent work has studied a new goal of balancing whole-match diversity and economic efficiency, where the objective is instead a monotone submodular function over the matching. These more general models are largely NP-hard. In this work, we develop a combinatorial algorithm that constructs provably-optimal diverse b-matchings in pseudo-polynomial time. Then, we show how to extend our algorithm to solve new variations of the diverse b-matching problem. We then compare directly, on real-world datasets, against the state-of-the-art, quadratic-programming-based approach to solving diverse b-matching problems and show that our method outperforms it in both speed and (anytime) solution quality.