Language-based Audio Retrieval with Co-Attention Networks

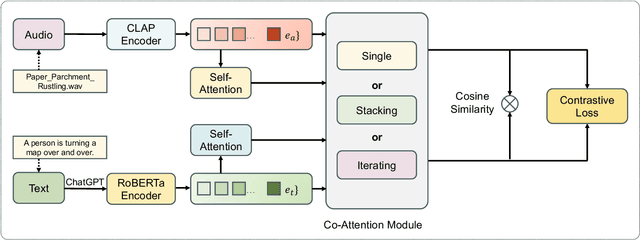
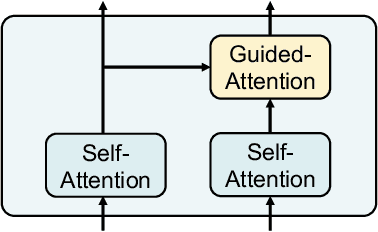
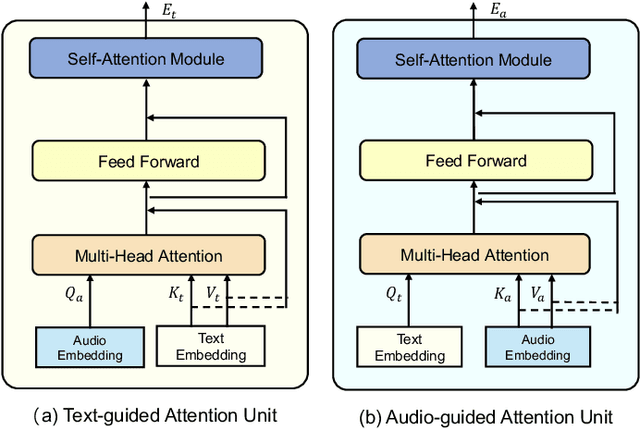
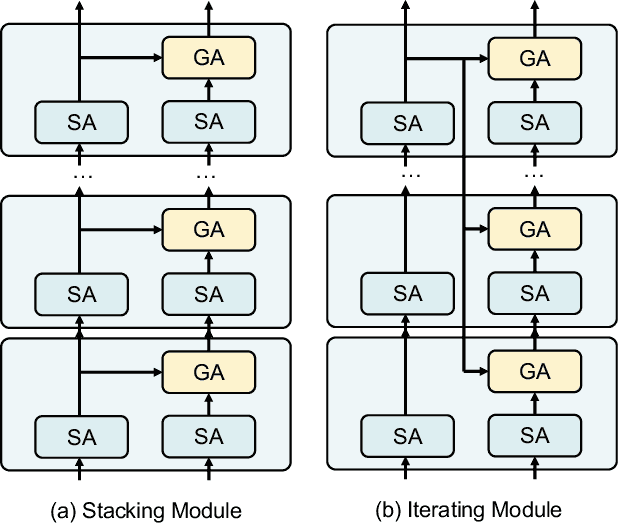
In recent years, user-generated audio content has proliferated across various media platforms, creating a growing need for efficient retrieval methods that allow users to search for audio clips using natural language queries. This task, known as language-based audio retrieval, presents significant challenges due to the complexity of learning semantic representations from heterogeneous data across both text and audio modalities. In this work, we introduce a novel framework for the language-based audio retrieval task that leverages co-attention mechanismto jointly learn meaningful representations from both modalities. To enhance the model's ability to capture fine-grained cross-modal interactions, we propose a cascaded co-attention architecture, where co-attention modules are stacked or iterated to progressively refine the semantic alignment between text and audio. Experiments conducted on two public datasets show that the proposed method can achieve better performance than the state-of-the-art method. Specifically, our best performed co-attention model achieves a 16.6% improvement in mean Average Precision on Clotho dataset, and a 15.1% improvement on AudioCaps.

Bayesian Inverse Problems with Conditional Sinkhorn Generative Adversarial Networks in Least Volume Latent Spaces

Solving inverse problems in scientific and engineering fields has long been intriguing and holds great potential for many applications, yet most techniques still struggle to address issues such as high dimensionality, nonlinearity and model uncertainty inherent in these problems. Recently, generative models such as Generative Adversarial Networks (GANs) have shown great potential in approximating complex high dimensional conditional distributions and have paved the way for characterizing posterior densities in Bayesian inverse problems, yet the problems' high dimensionality and high nonlinearity often impedes the model's training. In this paper we show how to tackle these issues with Least Volume--a novel unsupervised nonlinear dimension reduction method--that can learn to represent the given datasets with the minimum number of latent variables while estimating their intrinsic dimensions. Once the low dimensional latent spaces are identified, efficient and accurate training of conditional generative models becomes feasible, resulting in a latent conditional GAN framework for posterior inference. We demonstrate the power of the proposed methodology on a variety of applications including inversion of parameters in systems of ODEs and high dimensional hydraulic conductivities in subsurface flow problems, and reveal the impact of the observables' and unobservables' intrinsic dimensions on inverse problems.

Compressing Latent Space via Least Volume

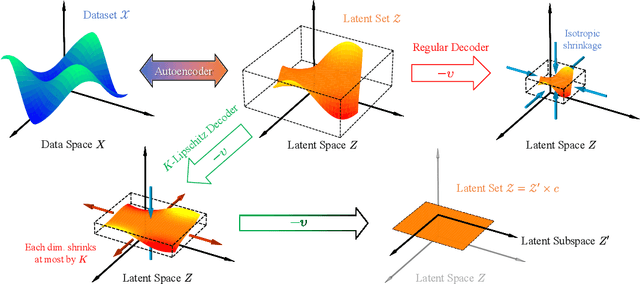
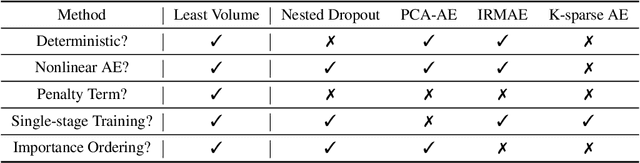
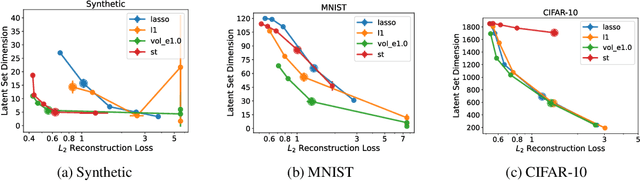
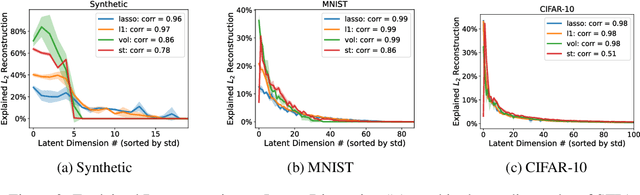
This paper introduces Least Volume-a simple yet effective regularization inspired by geometric intuition-that can reduce the necessary number of latent dimensions needed by an autoencoder without requiring any prior knowledge of the intrinsic dimensionality of the dataset. We show that the Lipschitz continuity of the decoder is the key to making it work, provide a proof that PCA is just a linear special case of it, and reveal that it has a similar PCA-like importance ordering effect when applied to nonlinear models. We demonstrate the intuition behind the regularization on some pedagogical toy problems, and its effectiveness on several benchmark problems, including MNIST, CIFAR-10 and CelebA.

Document Set Expansion with Positive-Unlabelled Learning Using Intractable Density Estimation

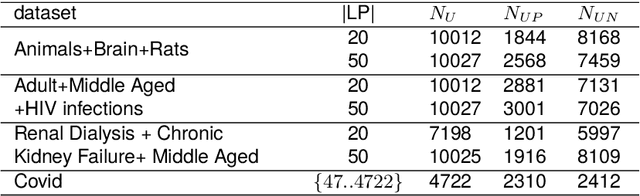
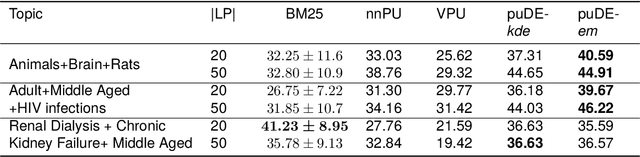
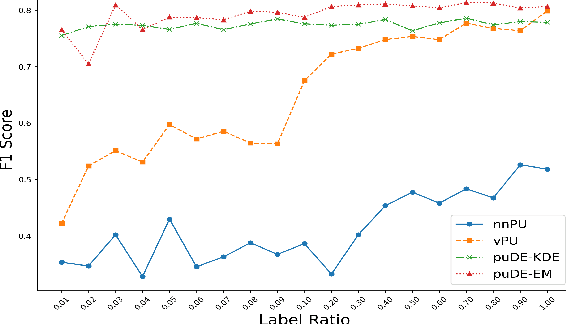
The Document Set Expansion (DSE) task involves identifying relevant documents from large collections based on a limited set of example documents. Previous research has highlighted Positive and Unlabeled (PU) learning as a promising approach for this task. However, most PU methods rely on the unrealistic assumption of knowing the class prior for positive samples in the collection. To address this limitation, this paper introduces a novel PU learning framework that utilizes intractable density estimation models. Experiments conducted on PubMed and Covid datasets in a transductive setting showcase the effectiveness of the proposed method for DSE. Code is available from https://github.com/Beautifuldog01/Document-set-expansion-puDE.

Document Set Expansion with Positive-Unlabeled Learning: A Density Estimation-based Approach

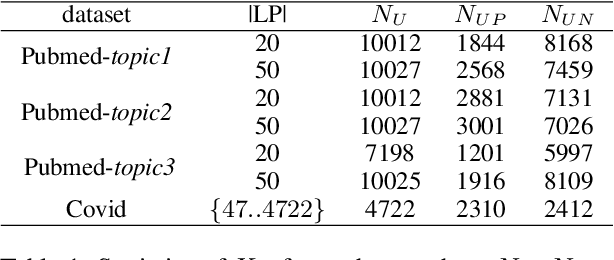
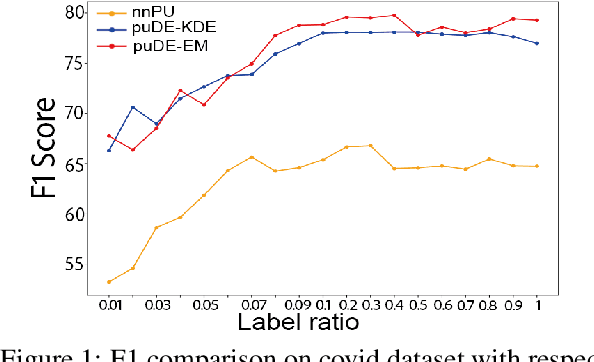
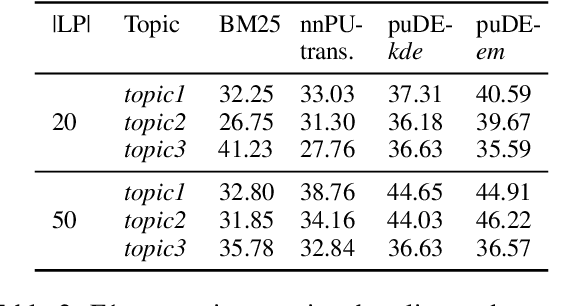
Document set expansion aims to identify relevant documents from a large collection based on a small set of documents that are on a fine-grained topic. Previous work shows that PU learning is a promising method for this task. However, some serious issues remain unresolved, i.e. typical challenges that PU methods suffer such as unknown class prior and imbalanced data, and the need for transductive experimental settings. In this paper, we propose a novel PU learning framework based on density estimation, called puDE, that can handle the above issues. The advantage of puDE is that it neither constrained to the SCAR assumption and nor require any class prior knowledge. We demonstrate the effectiveness of the proposed method using a series of real-world datasets and conclude that our method is a better alternative for the DSE task.