Deep Learning for Simultaneous Inference of Hydraulic and Transport Properties

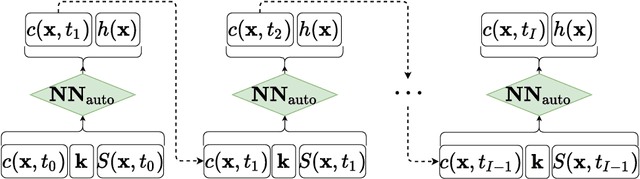
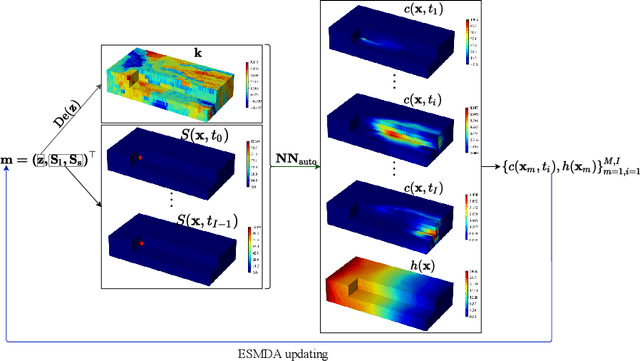
Identifying the heterogeneous conductivity field and reconstructing the contaminant release history are key aspects of subsurface remediation. Achieving these two goals with limited and noisy hydraulic head and concentration measurements is challenging. The obstacles include solving an inverse problem for high-dimensional parameters, and the high-computational cost needed for the repeated forward modeling. We use a convolutional adversarial autoencoder (CAAE) for the parameterization of the heterogeneous non-Gaussian conductivity field with a low-dimensional latent representation. Additionally, we trained a three-dimensional dense convolutional encoder-decoder (DenseED) network to serve as the forward surrogate for the flow and transport processes. Combining the CAAE and DenseED forward surrogate models, the ensemble smoother with multiple data assimilation (ESMDA) algorithm is used to sample from the Bayesian posterior distribution of the unknown parameters, forming a CAAE-DenseED-ESMDA inversion framework. We applied this CAAE-DenseED-ESMDA inversion framework in a three-dimensional contaminant source and conductivity field identification problem. A comparison of the inversion results from CAAE-ESMDA with physical flow and transport simulator and CAAE-DenseED-ESMDA is provided, showing that accurate reconstruction results were achieved with a much higher computational efficiency.

Inverse Aerodynamic Design of Gas Turbine Blades using Probabilistic Machine Learning

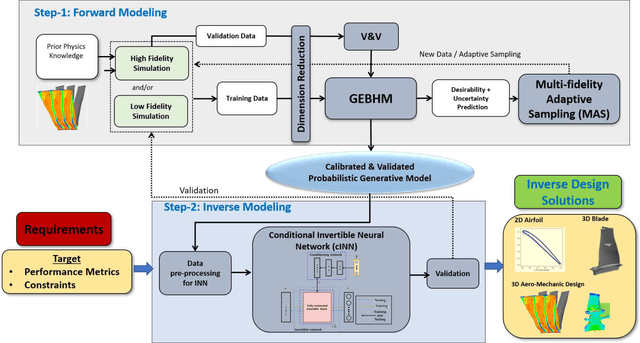
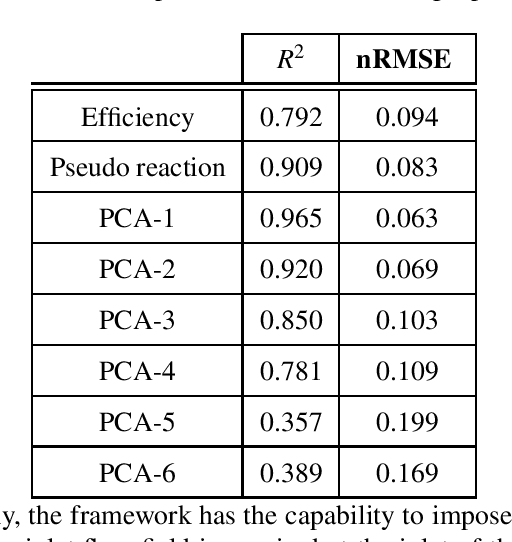
One of the critical components in Industrial Gas Turbines (IGT) is the turbine blade. Design of turbine blades needs to consider multiple aspects like aerodynamic efficiency, durability, safety and manufacturing, which make the design process sequential and iterative.The sequential nature of these iterations forces a long design cycle time, ranging from several months to years. Due to the reactionary nature of these iterations, little effort has been made to accumulate data in a manner that allows for deep exploration and understanding of the total design space. This is exemplified in the process of designing the individual components of the IGT resulting in a potential unrealized efficiency. To overcome the aforementioned challenges, we demonstrate a probabilistic inverse design machine learning framework (PMI), to carry out an explicit inverse design. PMI calculates the design explicitly without excessive costly iteration and overcomes the challenges associated with ill-posed inverse problems. In this work, the framework will be demonstrated on inverse aerodynamic design of three-dimensional turbine blades.

A Bayesian Multiscale Deep Learning Framework for Flows in Random Media

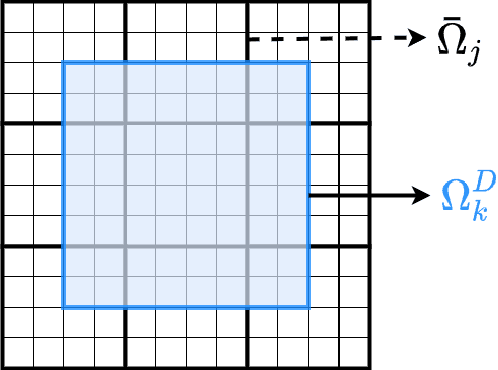
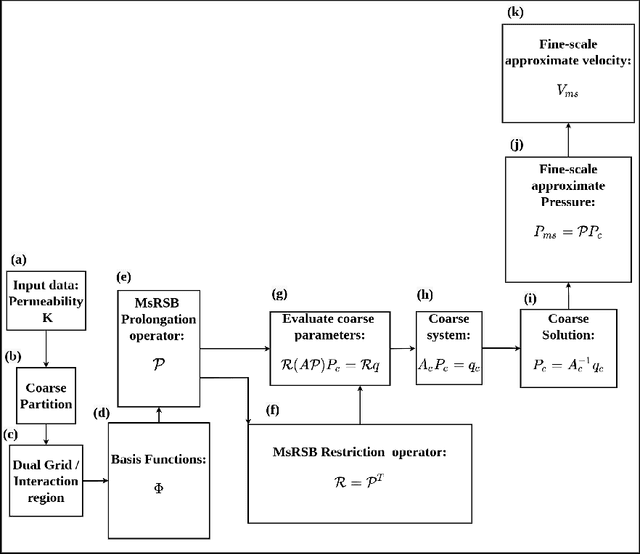
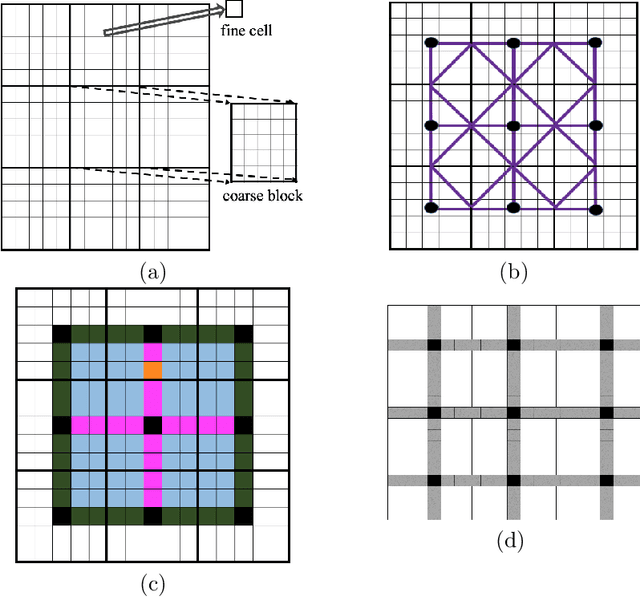
Fine-scale simulation of complex systems governed by multiscale partial differential equations (PDEs) is computationally expensive and various multiscale methods have been developed for addressing such problems. In addition, it is challenging to develop accurate surrogate and uncertainty quantification models for high-dimensional problems governed by stochastic multiscale PDEs using limited training data. In this work to address these challenges, we introduce a novel hybrid deep-learning and multiscale approach for stochastic multiscale PDEs with limited training data. For demonstration purposes, we focus on a porous media flow problem. We use an image-to-image supervised deep learning model to learn the mapping between the input permeability field and the multiscale basis functions. We introduce a Bayesian approach to this hybrid framework to allow us to perform uncertainty quantification and propagation tasks. The performance of this hybrid approach is evaluated with varying intrinsic dimensionality of the permeability field. Numerical results indicate that the hybrid network can efficiently predict well for high-dimensional inputs.

Bayesian multiscale deep generative model for the solution of high-dimensional inverse problems

Estimation of spatially-varying parameters for computationally expensive forward models governed by partial differential equations is addressed. A novel multiscale Bayesian inference approach is introduced based on deep probabilistic generative models. Such generative models provide a flexible representation by inferring on each scale a low-dimensional latent encoding while allowing hierarchical parameter generation from coarse- to fine-scales. Combining the multiscale generative model with Markov Chain Monte Carlo (MCMC), inference across scales is achieved enabling us to efficiently obtain posterior parameter samples at various scales. The estimation of coarse-scale parameters using a low-dimensional latent embedding captures global and notable parameter features using an inexpensive but inaccurate solver. MCMC sampling of the fine-scale parameters is enabled by utilizing the posterior information in the immediate coarser-scale. In this way, the global features are identified in the coarse-scale with inference of low-dimensional variables and inexpensive forward computation, and the local features are refined and corrected in the fine-scale. The developed method is demonstrated with two types of permeability estimation for flow in heterogeneous media. One is a Gaussian random field (GRF) with uncertain length scales, and the other is channelized permeability with the two regions defined by different GRFs. The obtained results indicate that the method allows high-dimensional parameter estimation while exhibiting stability, efficiency and accuracy.

Transformers for Modeling Physical Systems

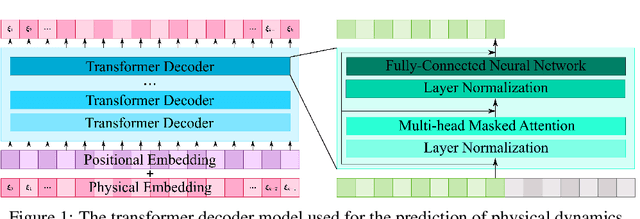
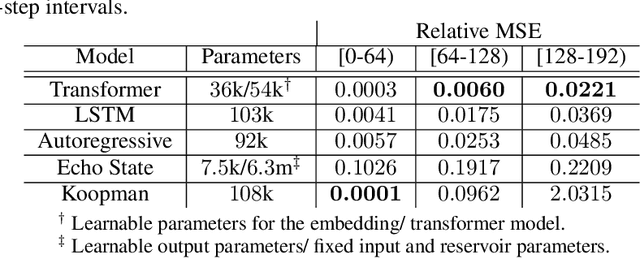
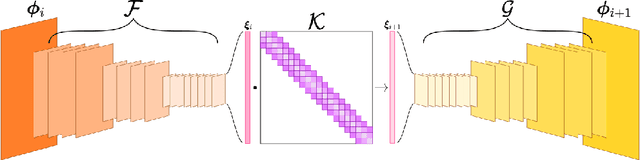
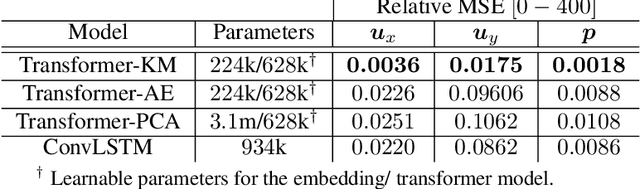
Transformers are widely used in neural language processing due to their ability to model longer-term dependencies in text. Although these models achieve state-of-the-art performance for many language related tasks, their applicability outside of the neural language processing field has been minimal. In this work, we propose the use of transformer models for the prediction of dynamical systems representative of physical phenomena. The use of Koopman based embeddings provide a unique and powerful method for projecting any dynamical system into a vector representation which can then be predicted by a transformer model. The proposed model is able to accurately predict various dynamical systems and outperform classical methods that are commonly used in the scientific machine learning literature.

Physics-Constrained Predictive Molecular Latent Space Discovery with Graph Scattering Variational Autoencoder

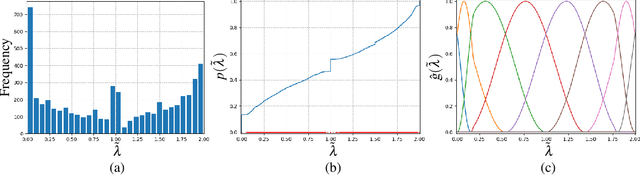
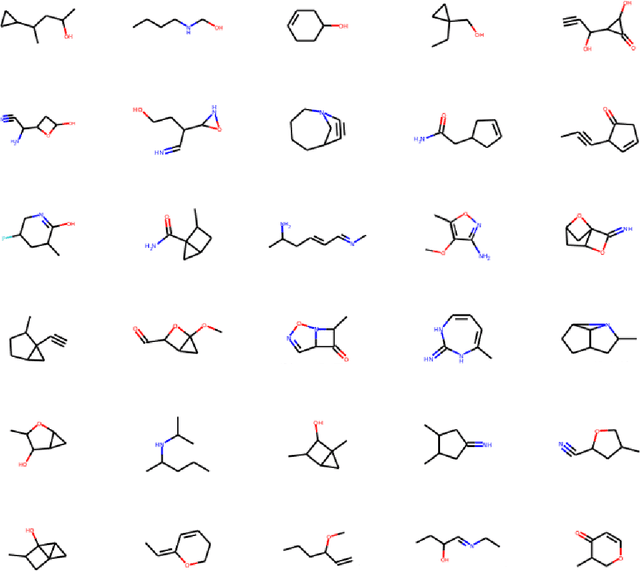
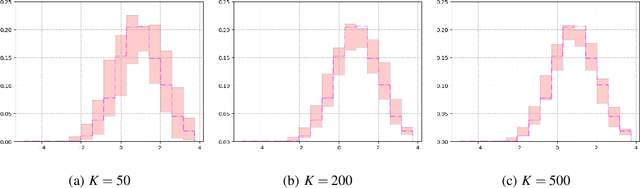
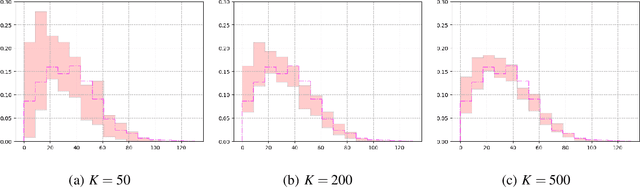
Recent advances in artificial intelligence have propelled the development of innovative computational materials modeling and design techniques. In particular, generative deep learning models have been used for molecular representation, discovery and design with applications ranging from drug discovery to solar cell development. In this work, we assess the predictive capabilities of a molecular generative model developed based on variational inference and graph theory. The encoder network is based on the scattering transform, which allows for a better generalization of the model in the presence of limited training data. The scattering layers incorporate adaptive spectral filters which are tailored to the training dataset based on the molecular graphs' spectra. The decoding network is a one-shot graph generative model that conditions atom types on molecular topology. We present a quantitative assessment of the latent space in terms of its predictive ability for organic molecules in the QM9 dataset. To account for the limited size training data set, a Bayesian formalism is considered that allows us capturing the uncertainties in the predicted properties.

Solving inverse problems using conditional invertible neural networks

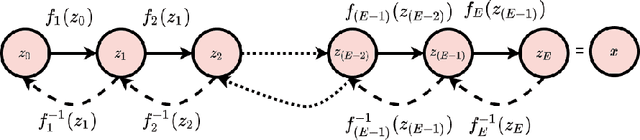
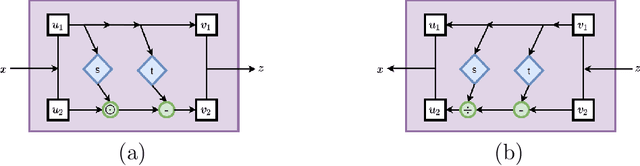
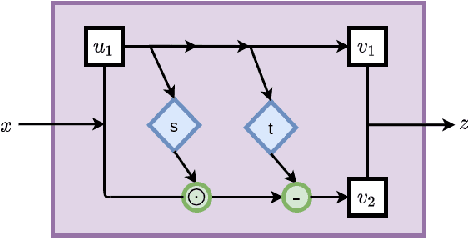
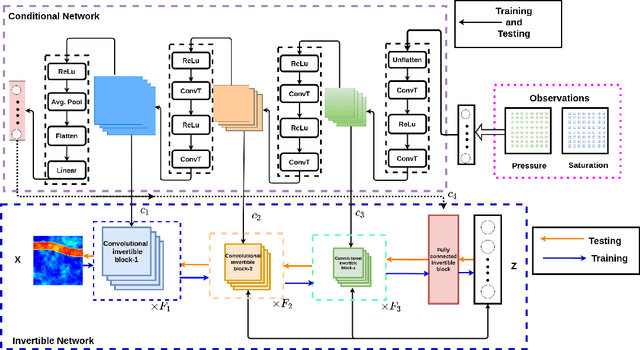
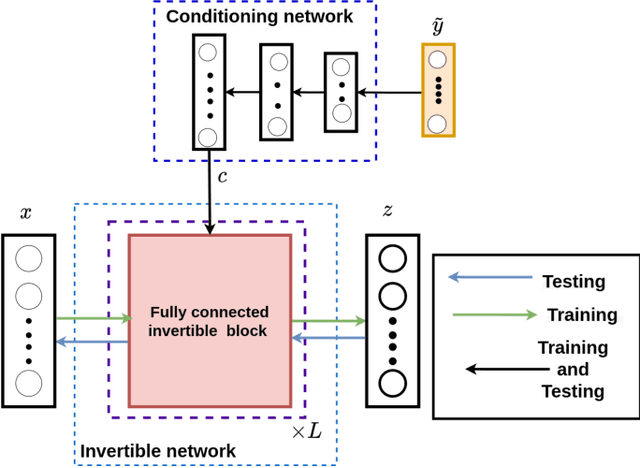
Inverse modeling for computing a high-dimensional spatially-varying property field from indirect sparse and noisy observations is a challenging problem. This is due to the complex physical system of interest often expressed in the form of multiscale PDEs, the high-dimensionality of the spatial property of interest, and the incomplete and noisy nature of observations. To address these challenges, we develop a model that maps the given observations to the unknown input field in the form of a surrogate model. This inverse surrogate model will then allow us to estimate the unknown input field for any given sparse and noisy output observations. Here, the inverse mapping is limited to a broad prior distribution of the input field with which the surrogate model is trained. In this work, we construct a two- and three-dimensional inverse surrogate models consisting of an invertible and a conditional neural network trained in an end-to-end fashion with limited training data. The invertible network is developed using a flow-based generative model. The developed inverse surrogate model is then applied for an inversion task of a multiphase flow problem where given the pressure and saturation observations the aim is to recover a high-dimensional non-Gaussian permeability field where the two facies consist of heterogeneous permeability and varying length-scales. For both the two- and three-dimensional surrogate models, the predicted sample realizations of the non-Gaussian permeability field are diverse with the predictive mean being close to the ground truth even when the model is trained with limited data.

Multi-fidelity Generative Deep Learning Turbulent Flows

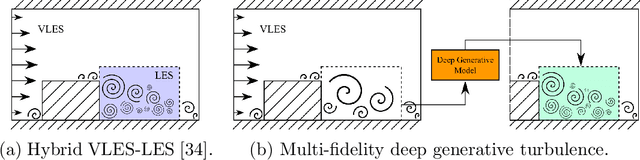
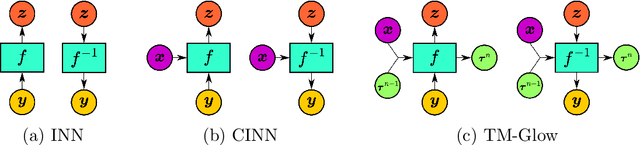
In computational fluid dynamics, there is an inevitable trade off between accuracy and computational cost. Low-fidelity simulations with coarse discretizations are computationally inexpensive, however, the resulting flow fields are often inaccurate. Alternatively, high-fidelity simulations can yield accurate predictions but at exponentially higher computational cost. In this work, a novel multi-fidelity deep generative model is introduced for the surrogate modeling of high-fidelity turbulent flow fields given the solution of a computationally inexpensive but inaccurate low-fidelity solver. The resulting surrogate is able to generate physically accurate turbulent realizations at a computational cost magnitudes lower than that of a high-fidelity simulation. The deep generative model developed is a conditional invertible neural network, built with normalizing flows, with recurrent LSTM connections that allow for stable training of transient systems with high predictive accuracy. The model is trained with a variational loss that combines both data-driven and physics-constrained learning. This deep generative model is applied to non-trivial high Reynolds number flows governed by the Navier-Stokes equations including turbulent flow over a backwards facing step at different Reynolds numbers and turbulent wake behind an array of bluff bodies. For both of these examples, the model is able to generate unique yet physically accurate turbulent fluid flows conditioned on an inexpensive low-fidelity solution.

Embedded-physics machine learning for coarse-graining and collective variable discovery without data

We present a novel learning framework that consistently embeds underlying physics while bypassing a significant drawback of most modern, data-driven coarse-grained approaches in the context of molecular dynamics (MD), i.e., the availability of big data. The generation of a sufficiently large training dataset poses a computationally demanding task, while complete coverage of the atomistic configuration space is not guaranteed. As a result, the explorative capabilities of data-driven coarse-grained models are limited and may yield biased "predictive" tools. We propose a novel objective based on reverse Kullback-Leibler divergence that fully incorporates the available physics in the form of the atomistic force field. Rather than separating model learning from the data-generation procedure - the latter relies on simulating atomistic motions governed by force fields - we query the atomistic force field at sample configurations proposed by the predictive coarse-grained model. Thus, learning relies on the evaluation of the force field but does not require any MD simulation. The resulting generative coarse-grained model serves as an efficient surrogate model for predicting atomistic configurations and estimating relevant observables. Beyond obtaining a predictive coarse-grained model, we demonstrate that in the discovered lower-dimensional representation, the collective variables (CVs) are related to physicochemical properties, which are essential for gaining understanding of unexplored complex systems. We demonstrate the algorithmic advances in terms of predictive ability and the physical meaning of the revealed CVs for a bimodal potential energy function and the alanine dipeptide.

Integration of adversarial autoencoders with residual dense convolutional networks for inversion of solute transport in non-Gaussian conductivity fields

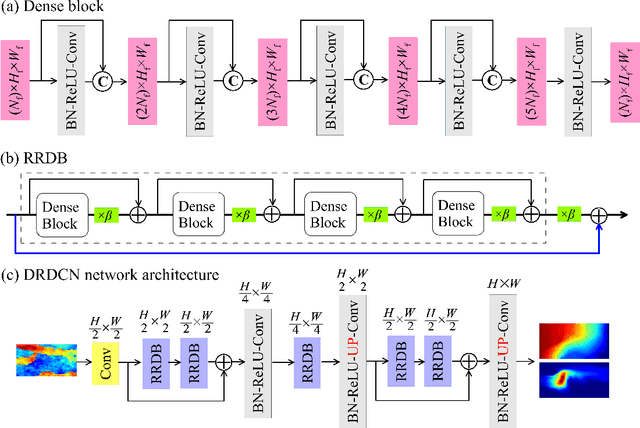
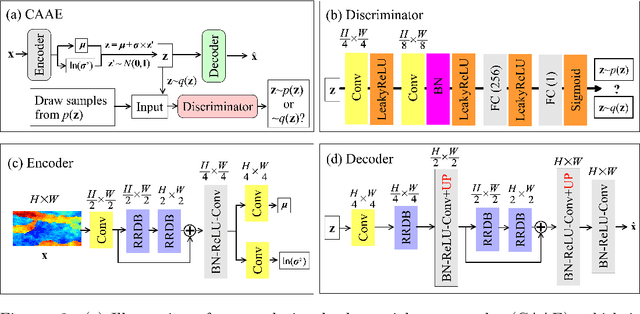
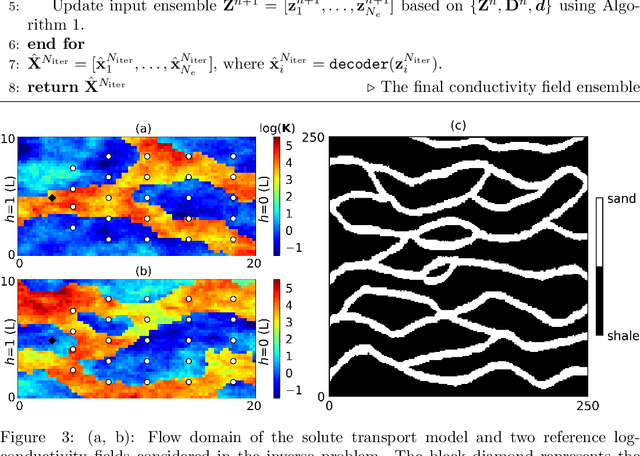
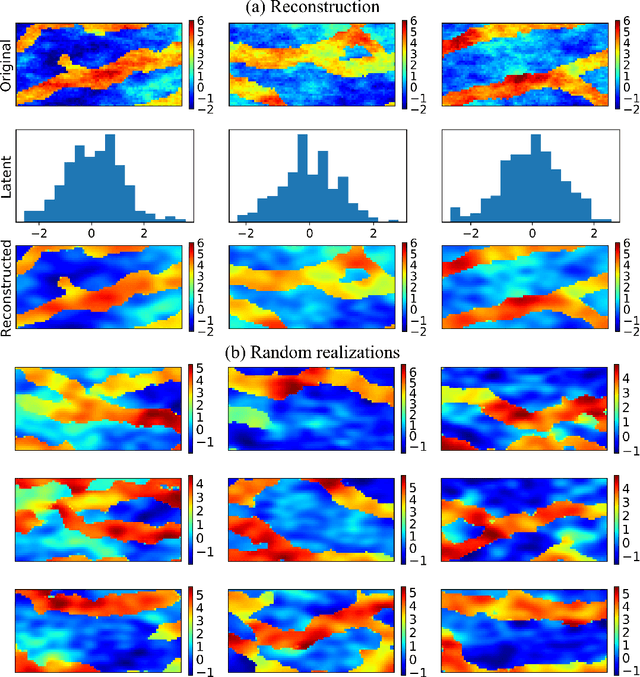
Characterization of a non-Gaussian channelized conductivity field in subsurface flow and transport modeling through inverse modeling usually leads to a high-dimensional inverse problem and requires repeated evaluations of the forward model. In this study, we develop a convolutional adversarial autoencoder (CAAE) network to parameterize the high-dimensional non-Gaussian conductivity fields using a low-dimensional latent representation and a deep residual dense convolutional network (DRDCN) to efficiently construct a surrogate model for the forward model. The two networks are both based on a multilevel residual learning architecture called residual-in-residual dense block. The multilevel residual learning strategy and the dense connection structure in the dense block ease the training of deep networks, enabling us to efficiently build deeper networks that have an essentially increased capacity for approximating mappings of very high-complexity. The CCAE and DRDCN networks are incorporated into an iterative local updating ensemble smoother to formulate an inversion framework. The integrated method is demonstrated using a synthetic solute transport model. Results indicate that CAAE is a robust parameterization method for the channelized conductivity fields with Gaussian conductivities within each facies. The DRDCN network is able to obtain an accurate surrogate model of the forward model with high-dimensional and highly-complex concentration fields using relatively limited training data. The CAAE paramterization approach and the DRDCN surrogate method together significantly reduce the number of forward model runs required to achieve accurate inversion results.