A Bayesian Multiscale Deep Learning Framework for Flows in Random Media
Paper and Code
Mar 08, 2021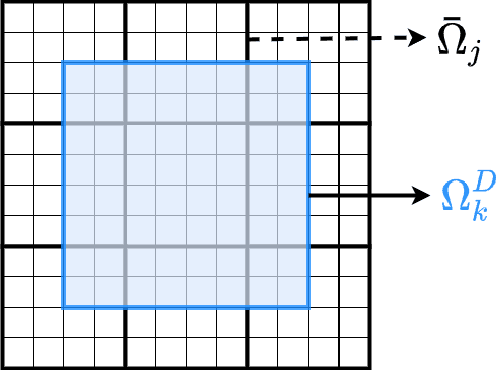

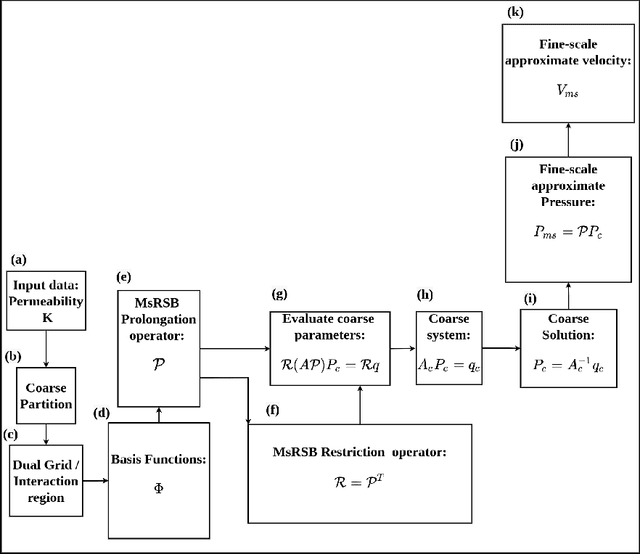
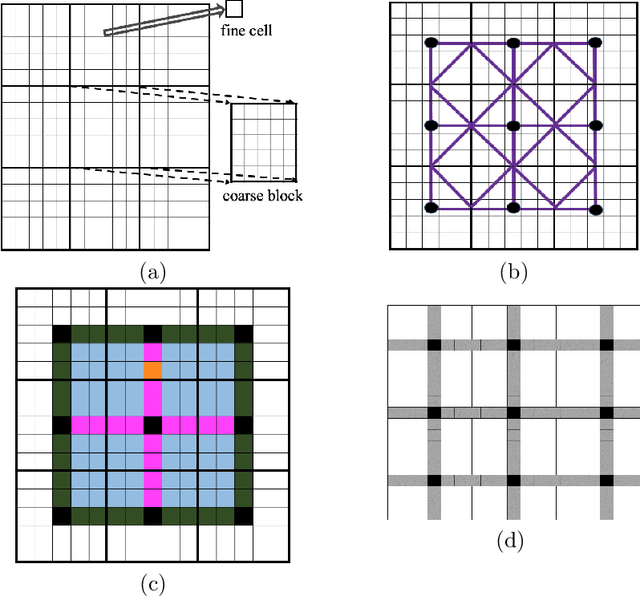
Fine-scale simulation of complex systems governed by multiscale partial differential equations (PDEs) is computationally expensive and various multiscale methods have been developed for addressing such problems. In addition, it is challenging to develop accurate surrogate and uncertainty quantification models for high-dimensional problems governed by stochastic multiscale PDEs using limited training data. In this work to address these challenges, we introduce a novel hybrid deep-learning and multiscale approach for stochastic multiscale PDEs with limited training data. For demonstration purposes, we focus on a porous media flow problem. We use an image-to-image supervised deep learning model to learn the mapping between the input permeability field and the multiscale basis functions. We introduce a Bayesian approach to this hybrid framework to allow us to perform uncertainty quantification and propagation tasks. The performance of this hybrid approach is evaluated with varying intrinsic dimensionality of the permeability field. Numerical results indicate that the hybrid network can efficiently predict well for high-dimensional inputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge