Condensed Stein Variational Gradient Descent for Uncertainty Quantification of Neural Networks

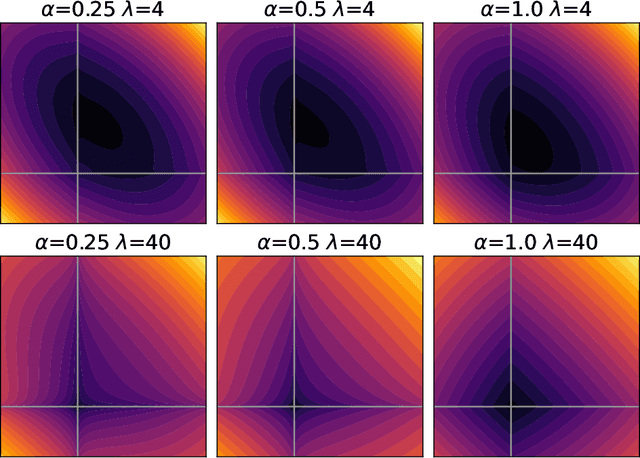
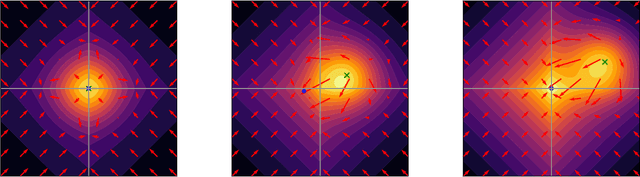
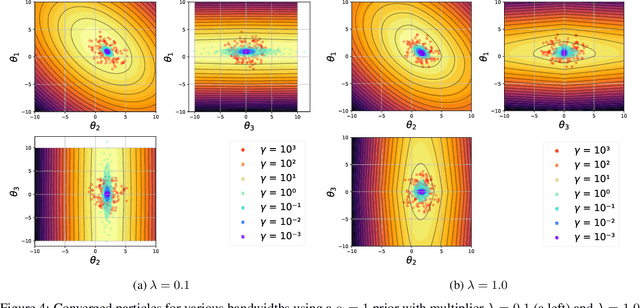
We propose a Stein variational gradient descent method to concurrently sparsify, train, and provide uncertainty quantification of a complexly parameterized model such as a neural network. It employs a graph reconciliation and condensation process to reduce complexity and increase similarity in the Stein ensemble of parameterizations. Therefore, the proposed condensed Stein variational gradient (cSVGD) method provides uncertainty quantification on parameters, not just outputs. Furthermore, the parameter reduction speeds up the convergence of the Stein gradient descent as it reduces the combinatorial complexity by aligning and differentiating the sensitivity to parameters. These properties are demonstrated with an illustrative example and an application to a representation problem in solid mechanics.

Improving the performance of Stein variational inference through extreme sparsification of physically-constrained neural network models

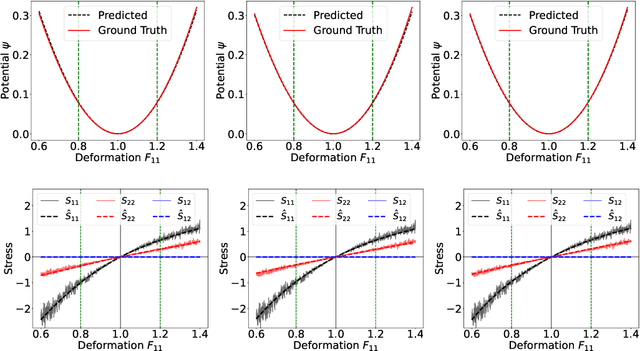
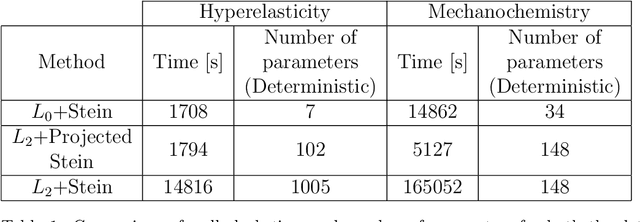
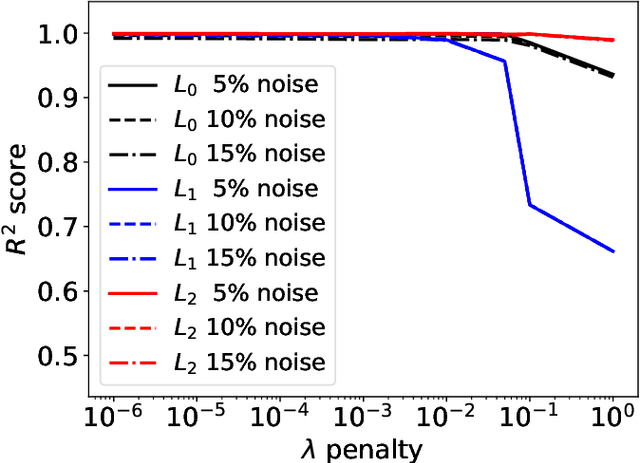
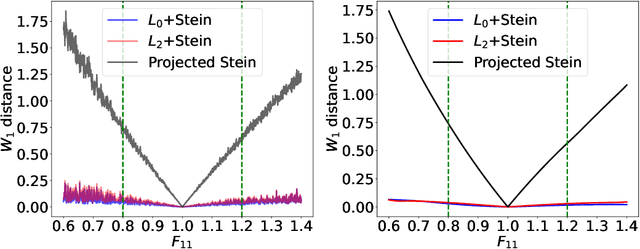
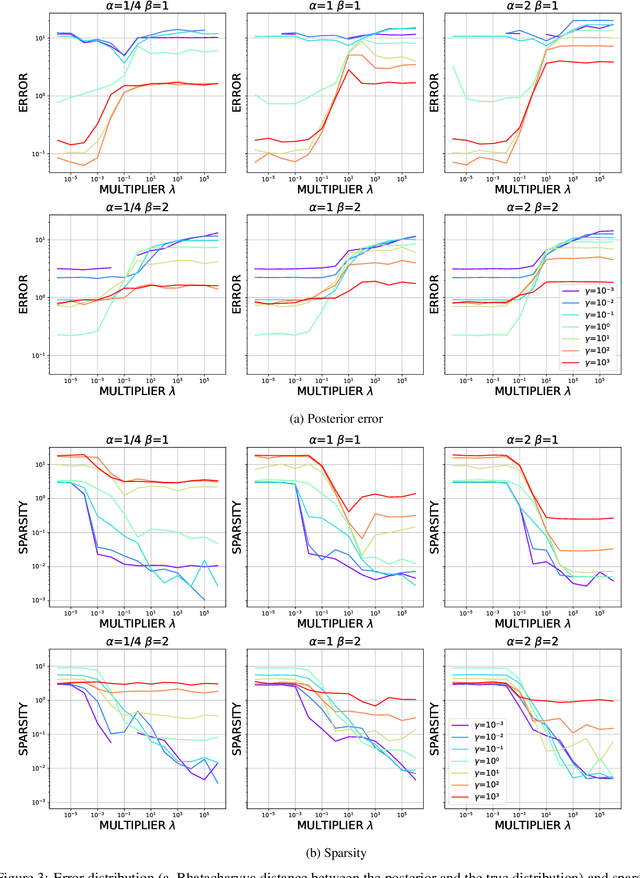
Most scientific machine learning (SciML) applications of neural networks involve hundreds to thousands of parameters, and hence, uncertainty quantification for such models is plagued by the curse of dimensionality. Using physical applications, we show that $L_0$ sparsification prior to Stein variational gradient descent ($L_0$+SVGD) is a more robust and efficient means of uncertainty quantification, in terms of computational cost and performance than the direct application of SGVD or projected SGVD methods. Specifically, $L_0$+SVGD demonstrates superior resilience to noise, the ability to perform well in extrapolated regions, and a faster convergence rate to an optimal solution.

A review on data-driven constitutive laws for solids

This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

A Bayesian Multiscale Deep Learning Framework for Flows in Random Media

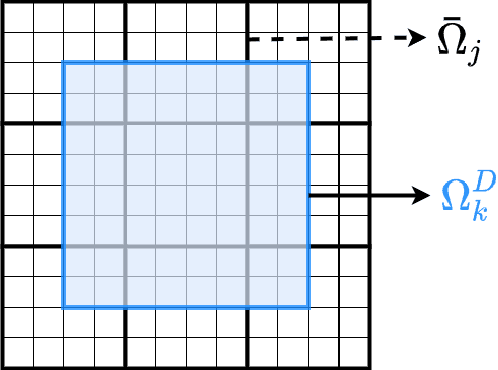
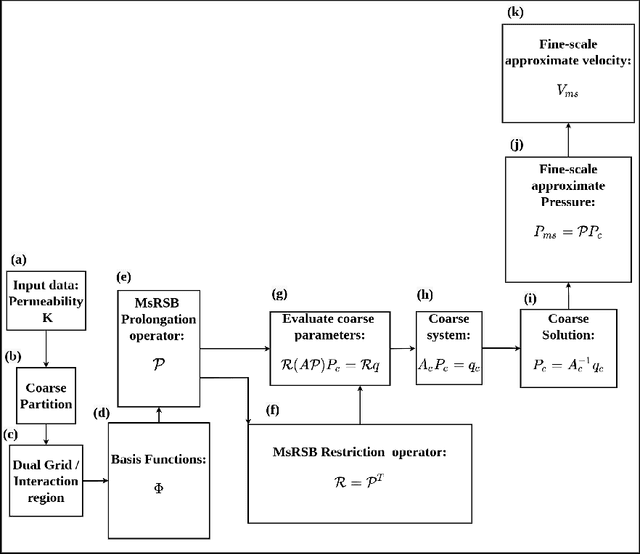
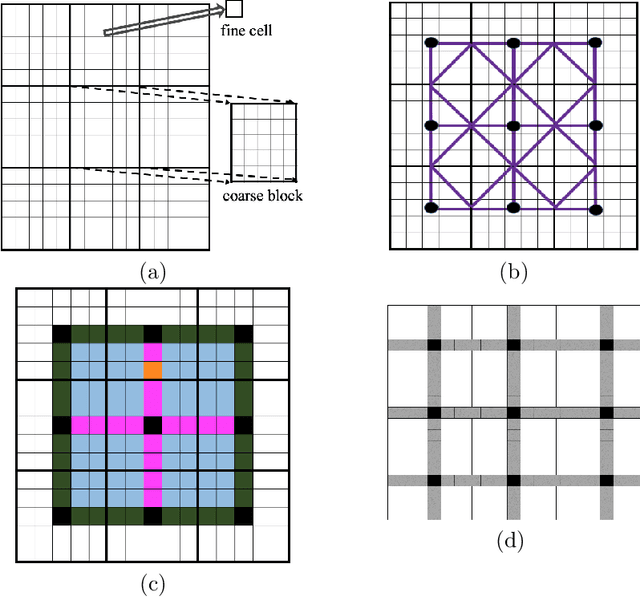
Fine-scale simulation of complex systems governed by multiscale partial differential equations (PDEs) is computationally expensive and various multiscale methods have been developed for addressing such problems. In addition, it is challenging to develop accurate surrogate and uncertainty quantification models for high-dimensional problems governed by stochastic multiscale PDEs using limited training data. In this work to address these challenges, we introduce a novel hybrid deep-learning and multiscale approach for stochastic multiscale PDEs with limited training data. For demonstration purposes, we focus on a porous media flow problem. We use an image-to-image supervised deep learning model to learn the mapping between the input permeability field and the multiscale basis functions. We introduce a Bayesian approach to this hybrid framework to allow us to perform uncertainty quantification and propagation tasks. The performance of this hybrid approach is evaluated with varying intrinsic dimensionality of the permeability field. Numerical results indicate that the hybrid network can efficiently predict well for high-dimensional inputs.

Solving inverse problems using conditional invertible neural networks

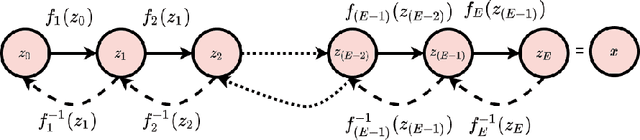
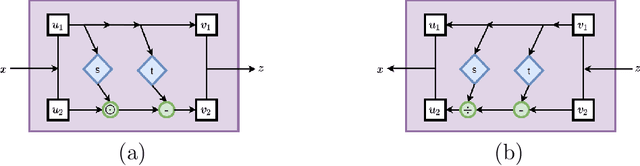
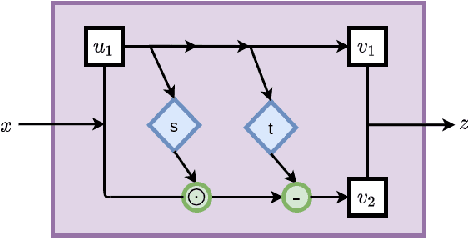
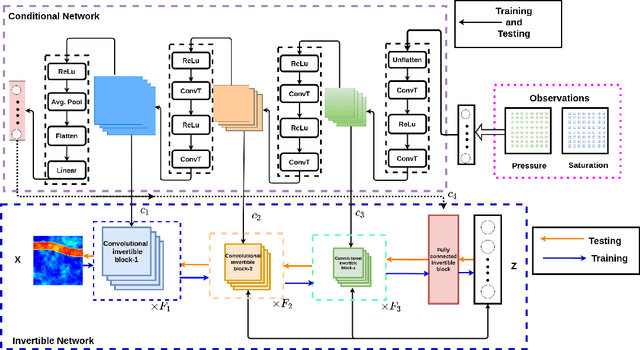
Inverse modeling for computing a high-dimensional spatially-varying property field from indirect sparse and noisy observations is a challenging problem. This is due to the complex physical system of interest often expressed in the form of multiscale PDEs, the high-dimensionality of the spatial property of interest, and the incomplete and noisy nature of observations. To address these challenges, we develop a model that maps the given observations to the unknown input field in the form of a surrogate model. This inverse surrogate model will then allow us to estimate the unknown input field for any given sparse and noisy output observations. Here, the inverse mapping is limited to a broad prior distribution of the input field with which the surrogate model is trained. In this work, we construct a two- and three-dimensional inverse surrogate models consisting of an invertible and a conditional neural network trained in an end-to-end fashion with limited training data. The invertible network is developed using a flow-based generative model. The developed inverse surrogate model is then applied for an inversion task of a multiphase flow problem where given the pressure and saturation observations the aim is to recover a high-dimensional non-Gaussian permeability field where the two facies consist of heterogeneous permeability and varying length-scales. For both the two- and three-dimensional surrogate models, the predicted sample realizations of the non-Gaussian permeability field are diverse with the predictive mean being close to the ground truth even when the model is trained with limited data.