Neural Chaos: A Spectral Stochastic Neural Operator

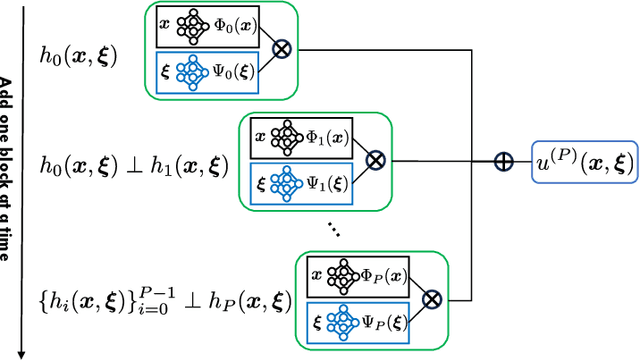
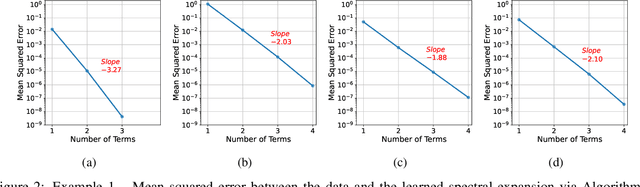
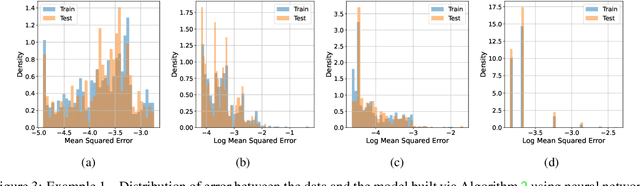
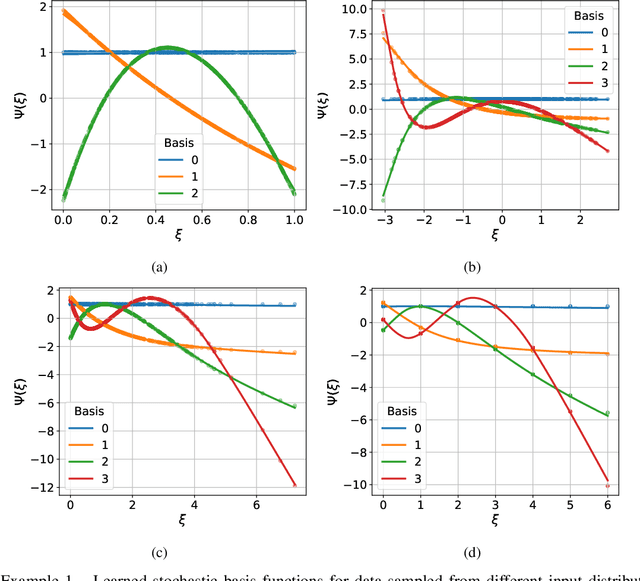
Building surrogate models with uncertainty quantification capabilities is essential for many engineering applications where randomness, such as variability in material properties, is unavoidable. Polynomial Chaos Expansion (PCE) is widely recognized as a to-go method for constructing stochastic solutions in both intrusive and non-intrusive ways. Its application becomes challenging, however, with complex or high-dimensional processes, as achieving accuracy requires higher-order polynomials, which can increase computational demands and or the risk of overfitting. Furthermore, PCE requires specialized treatments to manage random variables that are not independent, and these treatments may be problem-dependent or may fail with increasing complexity. In this work, we adopt the spectral expansion formalism used in PCE; however, we replace the classical polynomial basis functions with neural network (NN) basis functions to leverage their expressivity. To achieve this, we propose an algorithm that identifies NN-parameterized basis functions in a purely data-driven manner, without any prior assumptions about the joint distribution of the random variables involved, whether independent or dependent. The proposed algorithm identifies each NN-parameterized basis function sequentially, ensuring they are orthogonal with respect to the data distribution. The basis functions are constructed directly on the joint stochastic variables without requiring a tensor product structure. This approach may offer greater flexibility for complex stochastic models, while simplifying implementation compared to the tensor product structures typically used in PCE to handle random vectors. We demonstrate the effectiveness of the proposed scheme through several numerical examples of varying complexity and provide comparisons with classical PCE.

A Resolution Independent Neural Operator

The Deep operator network (DeepONet) is a powerful yet simple neural operator architecture that utilizes two deep neural networks to learn mappings between infinite-dimensional function spaces. This architecture is highly flexible, allowing the evaluation of the solution field at any location within the desired domain. However, it imposes a strict constraint on the input space, requiring all input functions to be discretized at the same locations; this limits its practical applications. In this work, we introduce a Resolution Independent Neural Operator (RINO) that provides a framework to make DeepONet resolution-independent, enabling it to handle input functions that are arbitrarily, but sufficiently finely, discretized. To this end, we propose a dictionary learning algorithm to adaptively learn a set of appropriate continuous basis functions, parameterized as implicit neural representations (INRs), from the input data. These basis functions are then used to project arbitrary input function data as a point cloud onto an embedding space (i.e., a vector space of finite dimensions) with dimensionality equal to the dictionary size, which can be directly used by DeepONet without any architectural changes. In particular, we utilize sinusoidal representation networks (SIRENs) as our trainable INR basis functions. We demonstrate the robustness and applicability of RINO in handling arbitrarily (but sufficiently richly) sampled input functions during both training and inference through several numerical examples.

A review on data-driven constitutive laws for solids

This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

Discovering interpretable elastoplasticity models via the neural polynomial method enabled symbolic regressions

Conventional neural network elastoplasticity models are often perceived as lacking interpretability. This paper introduces a two-step machine-learning approach that returns mathematical models interpretable by human experts. In particular, we introduce a surrogate model where yield surfaces are expressed in terms of a set of single-variable feature mappings obtained from supervised learning. A postprocessing step is then used to re-interpret the set of single-variable neural network mapping functions into mathematical form through symbolic regression. This divide-and-conquer approach provides several important advantages. First, it enables us to overcome the scaling issue of symbolic regression algorithms. From a practical perspective, it enhances the portability of learned models for partial differential equation solvers written in different programming languages. Finally, it enables us to have a concrete understanding of the attributes of the materials, such as convexity and symmetries of models, through automated derivations and reasoning. Numerical examples have been provided, along with an open-source code to enable third-party validation.

Manifold embedding data-driven mechanics

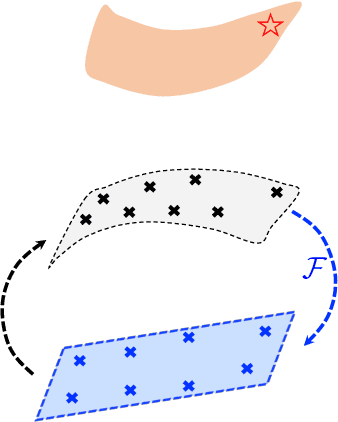
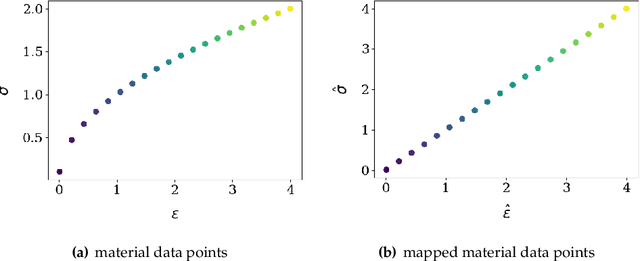
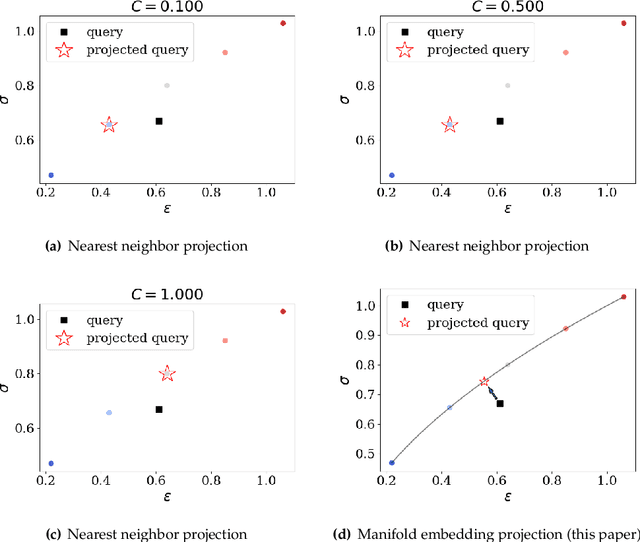
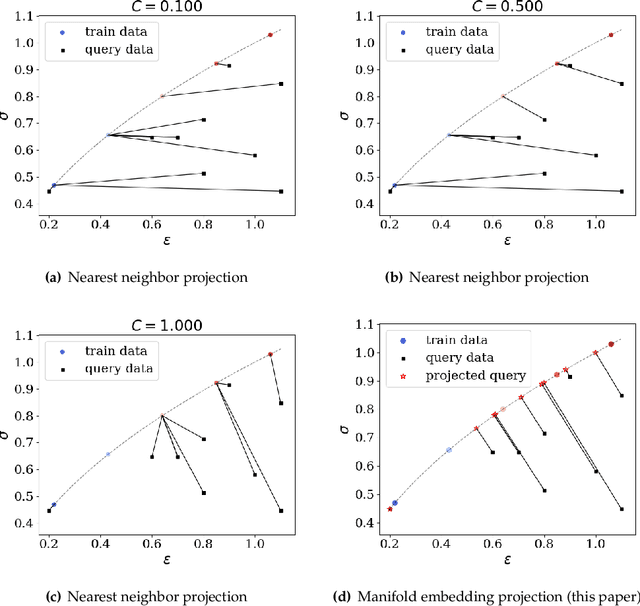
This article introduces a new data-driven approach that leverages a manifold embedding generated by the invertible neural network to improve the robustness, efficiency, and accuracy of the constitutive-law-free simulations with limited data. We achieve this by training a deep neural network to globally map data from the constitutive manifold onto a lower-dimensional Euclidean vector space. As such, we establish the relation between the norm of the mapped Euclidean vector space and the metric of the manifold and lead to a more physically consistent notion of distance for the material data. This treatment in return allows us to bypass the expensive combinatorial optimization, which may significantly speed up the model-free simulations when data are abundant and of high dimensions. Meanwhile, the learning of embedding also improves the robustness of the algorithm when the data is sparse or distributed unevenly in the parametric space. Numerical experiments are provided to demonstrate and measure the performance of the manifold embedding technique under different circumstances. Results obtained from the proposed method and those obtained via the classical energy norms are compared.

Training multi-objective/multi-task collocation physics-informed neural network with student/teachers transfer learnings

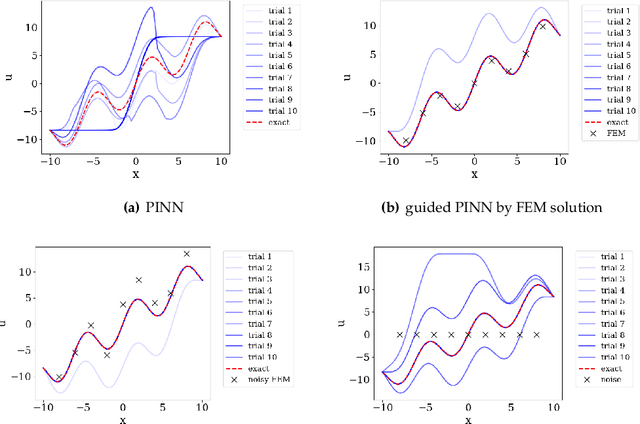
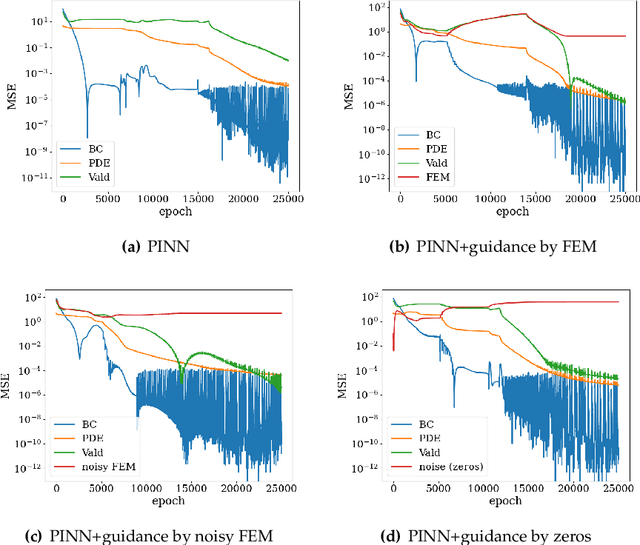
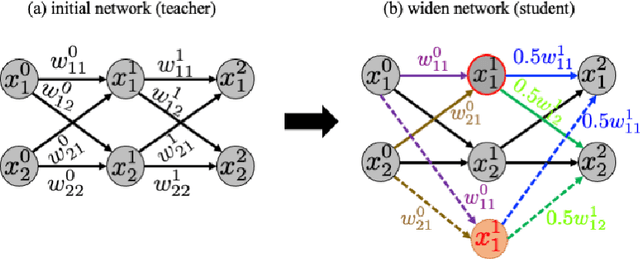
This paper presents a PINN training framework that employs (1) pre-training steps that accelerates and improve the robustness of the training of physics-informed neural network with auxiliary data stored in point clouds, (2) a net-to-net knowledge transfer algorithm that improves the weight initialization of the neural network and (3) a multi-objective optimization algorithm that may improve the performance of a physical-informed neural network with competing constraints. We consider the training and transfer and multi-task learning of physics-informed neural network (PINN) as multi-objective problems where the physics constraints such as the governing equation, boundary conditions, thermodynamic inequality, symmetry, and invariant properties, as well as point cloud used for pre-training can sometimes lead to conflicts and necessitating the seek of the Pareto optimal solution. In these situations, weighted norms commonly used to handle multiple constraints may lead to poor performance, while other multi-objective algorithms may scale poorly with increasing dimensionality. To overcome this technical barrier, we adopt the concept of vectorized objective function and modify a gradient descent approach to handle the issue of conflicting gradients. Numerical experiments are compared the benchmark boundary value problems solved via PINN. The performance of the proposed paradigm is compared against the classical equal-weighted norm approach. Our numerical experiments indicate that the brittleness and lack of robustness demonstrated in some PINN implementations can be overcome with the proposed strategy.

Data-driven discovery of interpretable causal relations for deep learning material laws with uncertainty propagation

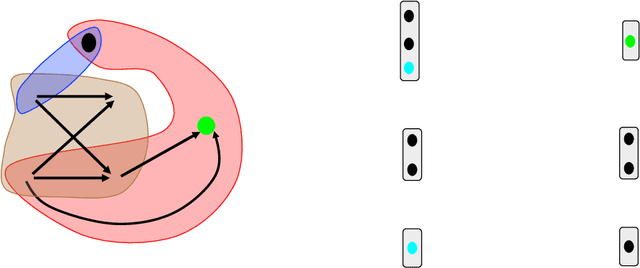
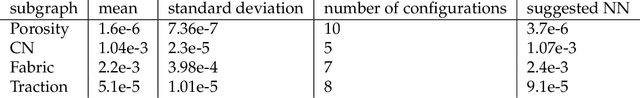
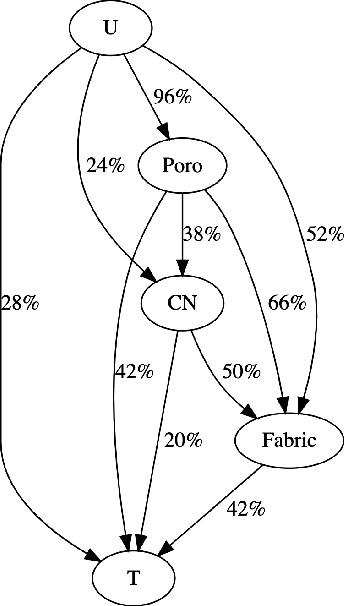
This paper presents a computational framework that generates ensemble predictive mechanics models with uncertainty quantification (UQ). We first develop a causal discovery algorithm to infer causal relations among time-history data measured during each representative volume element (RVE) simulation through a directed acyclic graph (DAG). With multiple plausible sets of causal relationships estimated from multiple RVE simulations, the predictions are propagated in the derived causal graph while using a deep neural network equipped with dropout layers as a Bayesian approximation for uncertainty quantification. We select two representative numerical examples (traction-separation laws for frictional interfaces, elastoplasticity models for granular assembles) to examine the accuracy and robustness of the proposed causal discovery method for the common material law predictions in civil engineering applications.

Equivariant geometric learning for digital rock physics: estimating formation factor and effective permeability tensors from Morse graph

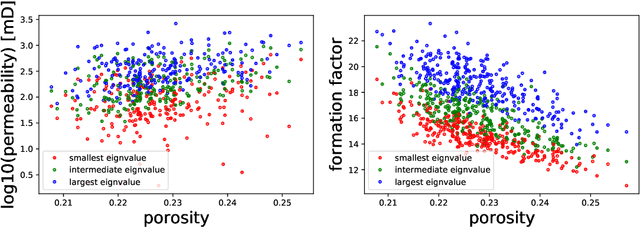
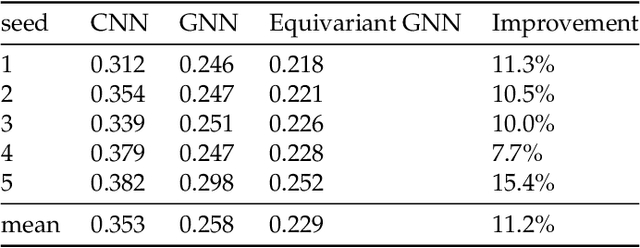
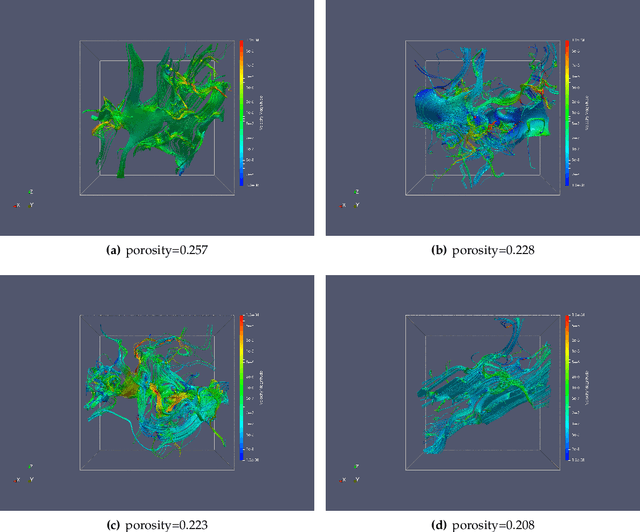
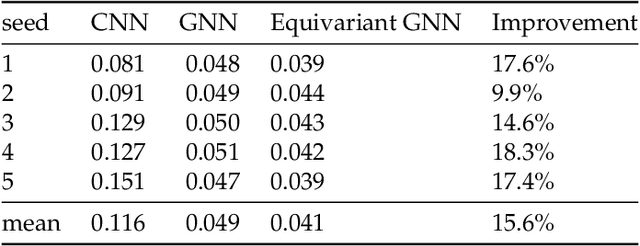
We present a SE(3)-equivariant graph neural network (GNN) approach that directly predicting the formation factor and effective permeability from micro-CT images. FFT solvers are established to compute both the formation factor and effective permeability, while the topology and geometry of the pore space are represented by a persistence-based Morse graph. Together, they constitute the database for training, validating, and testing the neural networks. While the graph and Euclidean convolutional approaches both employ neural networks to generate low-dimensional latent space to represent the features of the micro-structures for forward predictions, the SE(3) equivariant neural network is found to generate more accurate predictions, especially when the training data is limited. Numerical experiments have also shown that the new SE(3) approach leads to predictions that fulfill the material frame indifference whereas the predictions from classical convolutional neural networks (CNN) may suffer from spurious dependence on the coordinate system of the training data. Comparisons among predictions inferred from training the CNN and those from graph convolutional neural networks (GNN) with and without the equivariant constraint indicate that the equivariant graph neural network seems to perform better than the CNN and GNN without enforcing equivariant constraints.

An accelerated hybrid data-driven/model-based approach for poroelasticity problems with multi-fidelity multi-physics data

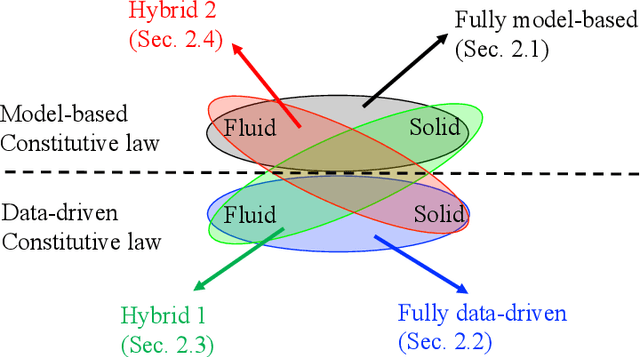
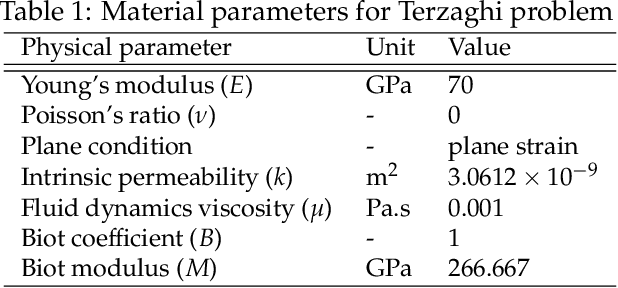
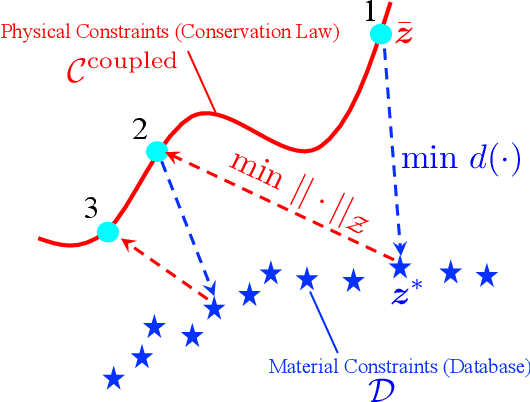
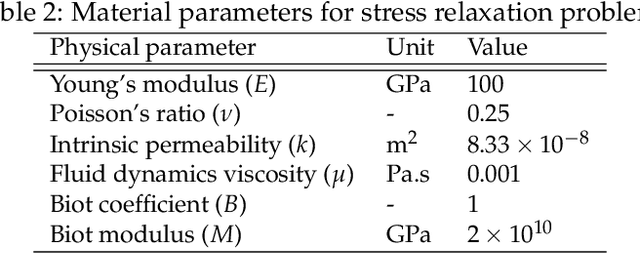
We present a hybrid model/model-free data-driven approach to solve poroelasticity problems. Extending the data-driven modeling framework originated from Kirchdoerfer and Ortiz (2016), we introduce one model-free and two hybrid model-based/data-driven formulations capable of simulating the coupled diffusion-deformation of fluid-infiltrating porous media with different amounts of available data. To improve the efficiency of the model-free data search, we introduce a distance-minimized algorithm accelerated by a k-dimensional tree search. To handle the different fidelities of the solid elasticity and fluid hydraulic constitutive responses, we introduce a hybridized model in which either the solid and the fluid solver can switch from a model-based to a model-free approach depending on the availability and the properties of the data. Numerical experiments are designed to verify the implementation and compare the performance of the proposed model to other alternatives.