Ran Ma
Adapter Naturally Serves as Decoupler for Cross-Domain Few-Shot Semantic Segmentation
Jun 09, 2025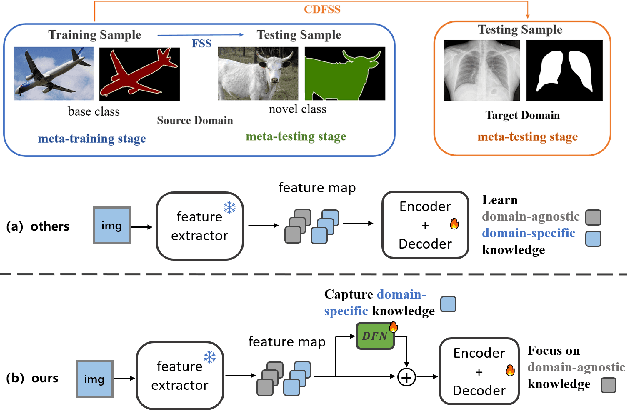
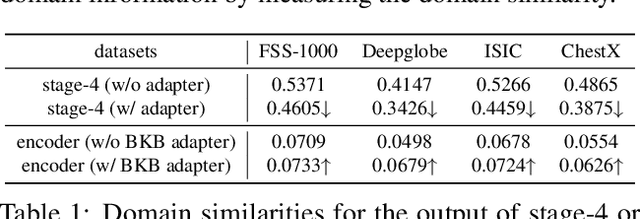
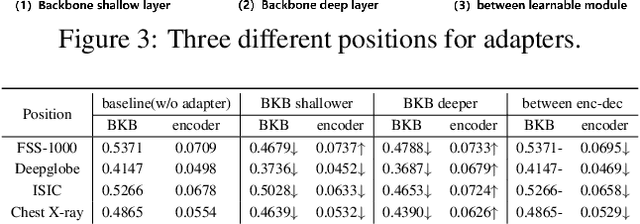
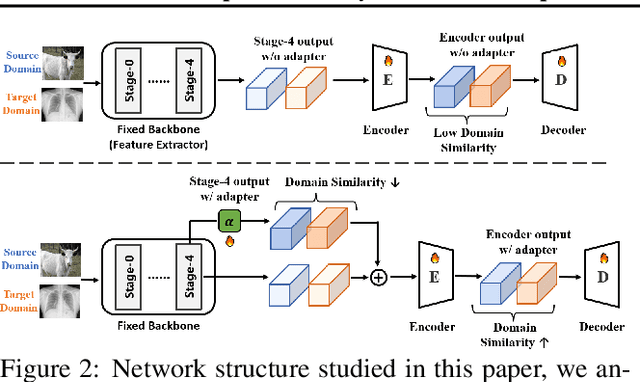
Abstract:Cross-domain few-shot segmentation (CD-FSS) is proposed to pre-train the model on a source-domain dataset with sufficient samples, and then transfer the model to target-domain datasets where only a few samples are available for efficient fine-tuning. There are majorly two challenges in this task: (1) the domain gap and (2) fine-tuning with scarce data. To solve these challenges, we revisit the adapter-based methods, and discover an intriguing insight not explored in previous works: the adapter not only helps the fine-tuning of downstream tasks but also naturally serves as a domain information decoupler. Then, we delve into this finding for an interpretation, and find the model's inherent structure could lead to a natural decoupling of domain information. Building upon this insight, we propose the Domain Feature Navigator (DFN), which is a structure-based decoupler instead of loss-based ones like current works, to capture domain-specific information, thereby directing the model's attention towards domain-agnostic knowledge. Moreover, to prevent the potential excessive overfitting of DFN during the source-domain training, we further design the SAM-SVN method to constrain DFN from learning sample-specific knowledge. On target domains, we freeze the model and fine-tune the DFN to learn target-specific knowledge specific. Extensive experiments demonstrate that our method surpasses the state-of-the-art method in CD-FSS significantly by 2.69% and 4.68% MIoU in 1-shot and 5-shot scenarios, respectively.
NTIRE 2025 Challenge on Cross-Domain Few-Shot Object Detection: Methods and Results
Apr 14, 2025Abstract:Cross-Domain Few-Shot Object Detection (CD-FSOD) poses significant challenges to existing object detection and few-shot detection models when applied across domains. In conjunction with NTIRE 2025, we organized the 1st CD-FSOD Challenge, aiming to advance the performance of current object detectors on entirely novel target domains with only limited labeled data. The challenge attracted 152 registered participants, received submissions from 42 teams, and concluded with 13 teams making valid final submissions. Participants approached the task from diverse perspectives, proposing novel models that achieved new state-of-the-art (SOTA) results under both open-source and closed-source settings. In this report, we present an overview of the 1st NTIRE 2025 CD-FSOD Challenge, highlighting the proposed solutions and summarizing the results submitted by the participants.
Reconstruction Target Matters in Masked Image Modeling for Cross-Domain Few-Shot Learning
Dec 26, 2024



Abstract:Cross-Domain Few-Shot Learning (CDFSL) requires the model to transfer knowledge from the data-abundant source domain to data-scarce target domains for fast adaptation, where the large domain gap makes CDFSL a challenging problem. Masked Autoencoder (MAE) excels in effectively using unlabeled data and learning image's global structures, enhancing model generalization and robustness. However, in the CDFSL task with significant domain shifts, we find MAE even shows lower performance than the baseline supervised models. In this paper, we first delve into this phenomenon for an interpretation. We find that MAE tends to focus on low-level domain information during reconstructing pixels while changing the reconstruction target to token features could mitigate this problem. However, not all features are beneficial, as we then find reconstructing high-level features can hardly improve the model's transferability, indicating a trade-off between filtering domain information and preserving the image's global structure. In all, the reconstruction target matters for the CDFSL task. Based on the above findings and interpretations, we further propose Domain-Agnostic Masked Image Modeling (DAMIM) for the CDFSL task. DAMIM includes an Aggregated Feature Reconstruction module to automatically aggregate features for reconstruction, with balanced learning of domain-agnostic information and images' global structure, and a Lightweight Decoder module to further benefit the encoder's generalizability. Experiments on four CDFSL datasets demonstrate that our method achieves state-of-the-art performance.
MD-inferred neural network monoclinic finite-strain hyperelasticity models for $β$-HMX: Sobolev training and validation against physical constraints
Nov 29, 2021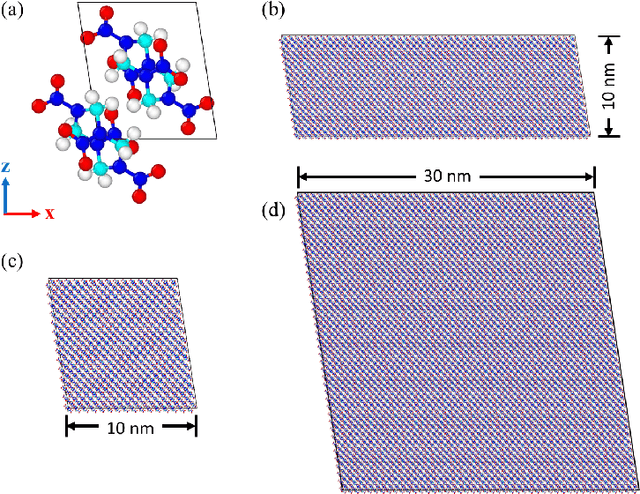



Abstract:We present a machine learning framework to train and validate neural networks to predict the anisotropic elastic response of the monoclinic organic molecular crystal $\beta$-HMX in the geometrical nonlinear regime. A filtered molecular dynamic (MD) simulations database is used to train the neural networks with a Sobolev norm that uses the stress measure and a reference configuration to deduce the elastic stored energy functional. To improve the accuracy of the elasticity tangent predictions originating from the learned stored energy, a transfer learning technique is used to introduce additional tangential constraints from the data while necessary conditions (e.g. strong ellipticity, crystallographic symmetry) for the correctness of the model are either introduced as additional physical constraints or incorporated in the validation tests. Assessment of the neural networks is based on (1) the accuracy with which they reproduce the bottom-line constitutive responses predicted by MD, (2) detailed examination of their stability and uniqueness, and (3) admissibility of the predicted responses with respect to continuum mechanics theory in the finite-deformation regime. We compare the neural networks' training efficiency under different Sobolev constraints and assess the models' accuracy and robustness against MD benchmarks for $\beta$-HMX.
Equivariant geometric learning for digital rock physics: estimating formation factor and effective permeability tensors from Morse graph
Apr 12, 2021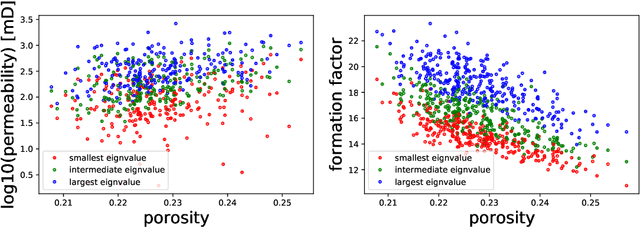
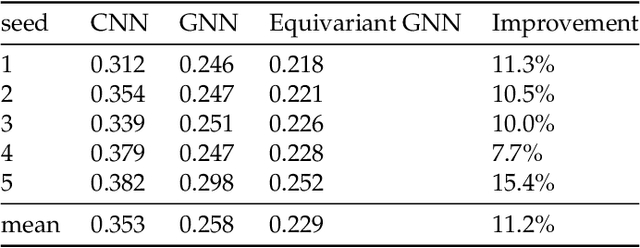
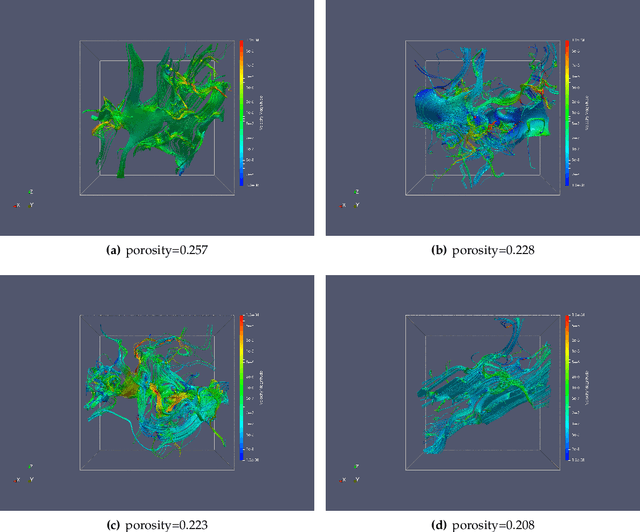
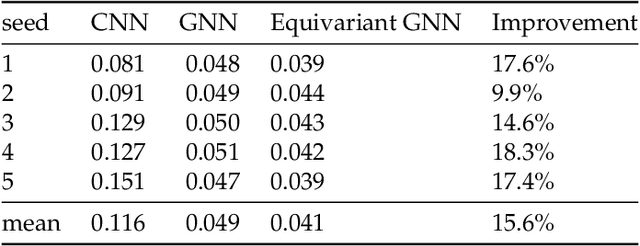
Abstract:We present a SE(3)-equivariant graph neural network (GNN) approach that directly predicting the formation factor and effective permeability from micro-CT images. FFT solvers are established to compute both the formation factor and effective permeability, while the topology and geometry of the pore space are represented by a persistence-based Morse graph. Together, they constitute the database for training, validating, and testing the neural networks. While the graph and Euclidean convolutional approaches both employ neural networks to generate low-dimensional latent space to represent the features of the micro-structures for forward predictions, the SE(3) equivariant neural network is found to generate more accurate predictions, especially when the training data is limited. Numerical experiments have also shown that the new SE(3) approach leads to predictions that fulfill the material frame indifference whereas the predictions from classical convolutional neural networks (CNN) may suffer from spurious dependence on the coordinate system of the training data. Comparisons among predictions inferred from training the CNN and those from graph convolutional neural networks (GNN) with and without the equivariant constraint indicate that the equivariant graph neural network seems to perform better than the CNN and GNN without enforcing equivariant constraints.
Geometric deep learning for computational mechanics Part I: Anisotropic Hyperelasticity
Jan 08, 2020



Abstract:This paper is the first attempt to use geometric deep learning and Sobolev training to incorporate non-Euclidean microstructural data such that anisotropic hyperelastic material machine learning models can be trained in the finite deformation range. While traditional hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as porosity averaged orientation of constitutes, these measures cannot reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of weighted graph as a new mean to store topological information, such as the connectivity of anisotropic grains in assembles. Then, by leveraging a graph convolutional deep neural network architecture in the spectral domain, we introduce a mechanism to incorporate these non-Euclidean weighted graph data directly as input for training and for predicting the elastic responses of materials with complex microstructures. To ensure smoothness and prevent non-convexity of the trained stored energy functional, we introduce a Sobolev training technique for neural networks such that stress measure is obtained implicitly from taking directional derivatives of the trained energy functional. By optimizing the neural network to approximate both the energy functional output and the stress measure, we introduce a training procedure the improves efficiency and generalize the learned energy functional for different microstructures. The trained hybrid neural network model is then used to generate new stored energy functional for unseen microstructures in a parametric study to predict the influence of elastic anisotropy on the nucleation and propagation of fracture in the brittle regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge