The Best of Both Worlds: Hybridizing Neural Operators and Solvers for Stable Long-Horizon Inference

Numerical simulation of time-dependent partial differential equations (PDEs) is central to scientific and engineering applications, but high-fidelity solvers are often prohibitively expensive for long-horizon or time-critical settings. Neural operator (NO) surrogates offer fast inference across parametric and functional inputs; however, most autoregressive NO frameworks remain vulnerable to compounding errors, and ensemble-averaged metrics provide limited guarantees for individual inference trajectories. In practice, error accumulation can become unacceptable beyond the training horizon, and existing methods lack mechanisms for online monitoring or correction. To address this gap, we propose ANCHOR (Adaptive Numerical Correction for High-fidelity Operator Rollouts), an online, instance-aware hybrid inference framework for stable long-horizon prediction of nonlinear, time-dependent PDEs. ANCHOR treats a pretrained NO as the primary inference engine and adaptively couples it with a classical numerical solver using a physics-informed, residual-based error estimator. Inspired by adaptive time-stepping in numerical analysis, ANCHOR monitors an exponential moving average (EMA) of the normalized PDE residual to detect accumulating error and trigger corrective solver interventions without requiring access to ground-truth solutions. We show that the EMA-based estimator correlates strongly with the true relative L2 error, enabling data-free, instance-aware error control during inference. Evaluations on four canonical PDEs: 1D and 2D Burgers', 2D Allen-Cahn, and 3D heat conduction, demonstrate that ANCHOR reliably bounds long-horizon error growth, stabilizes extrapolative rollouts, and significantly improves robustness over standalone neural operators, while remaining substantially more efficient than high-fidelity numerical solvers.

Importance of localized dilatation and distensibility in identifying determinants of thoracic aortic aneurysm with neural operators

Thoracic aortic aneurysms (TAAs) arise from diverse mechanical and mechanobiological disruptions to the aortic wall that increase the risk of dissection or rupture. Evidence links TAA development to dysfunctions in the aortic mechanotransduction axis, including loss of elastic fiber integrity and cell-matrix connections. Because distinct insults create different mechanical vulnerabilities, there is a critical need to identify interacting factors that drive progression. Here, we use a finite element framework to generate synthetic TAAs from hundreds of heterogeneous insults spanning varying degrees of elastic fiber damage and impaired mechanosensing. From these simulations, we construct spatial maps of localized dilatation and distensibility to train neural networks that predict the initiating combined insult. We compare several architectures (Deep Operator Networks, UNets, and Laplace Neural Operators) and multiple input data formats to define a standard for future subject-specific modeling. We also quantify predictive performance when networks are trained using only geometric data (dilatation) versus both geometric and mechanical data (dilatation plus distensibility). Across all networks, prediction errors are significantly higher when trained on dilatation alone, underscoring the added value of distensibility information. Among the tested models, UNet consistently provides the highest accuracy across all data formats. These findings highlight the importance of acquiring full-field measurements of both dilatation and distensibility in TAA assessment to reveal the mechanobiological drivers of disease and support the development of personalized treatment strategies.

Physics-Informed Time-Integrated DeepONet: Temporal Tangent Space Operator Learning for High-Accuracy Inference

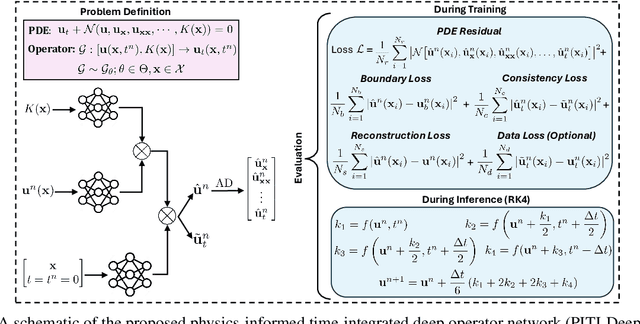
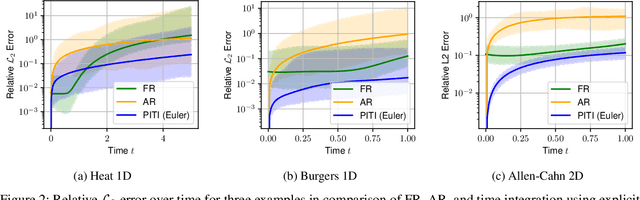
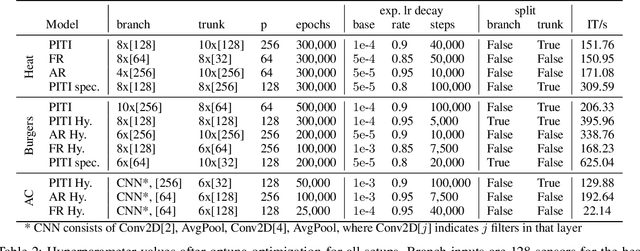
Accurately modeling and inferring solutions to time-dependent partial differential equations (PDEs) over extended horizons remains a core challenge in scientific machine learning. Traditional full rollout (FR) methods, which predict entire trajectories in one pass, often fail to capture the causal dependencies and generalize poorly outside the training time horizon. Autoregressive (AR) approaches, evolving the system step by step, suffer from error accumulation, limiting long-term accuracy. These shortcomings limit the long-term accuracy and reliability of both strategies. To address these issues, we introduce the Physics-Informed Time-Integrated Deep Operator Network (PITI-DeepONet), a dual-output architecture trained via fully physics-informed or hybrid physics- and data-driven objectives to ensure stable, accurate long-term evolution well beyond the training horizon. Instead of forecasting future states, the network learns the time-derivative operator from the current state, integrating it using classical time-stepping schemes to advance the solution in time. Additionally, the framework can leverage residual monitoring during inference to estimate prediction quality and detect when the system transitions outside the training domain. Applied to benchmark problems, PITI-DeepONet shows improved accuracy over extended inference time horizons when compared to traditional methods. Mean relative $\mathcal{L}_2$ errors reduced by 84% (vs. FR) and 79% (vs. AR) for the one-dimensional heat equation; by 87% (vs. FR) and 98% (vs. AR) for the one-dimensional Burgers equation; and by 42% (vs. FR) and 89% (vs. AR) for the two-dimensional Allen-Cahn equation. By moving beyond classic FR and AR schemes, PITI-DeepONet paves the way for more reliable, long-term integration of complex, time-dependent PDEs.

TI-DeepONet: Learnable Time Integration for Stable Long-Term Extrapolation

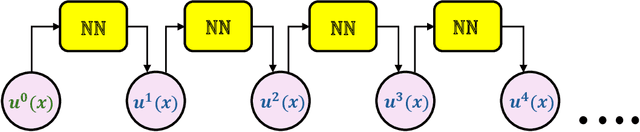
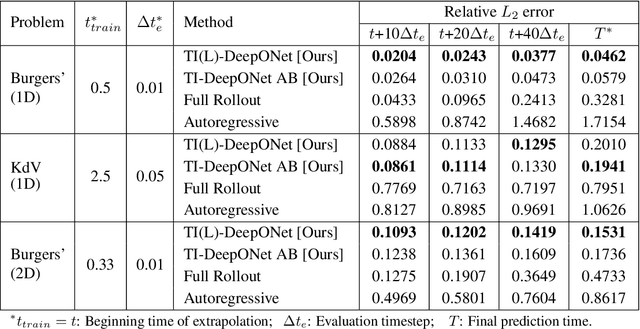
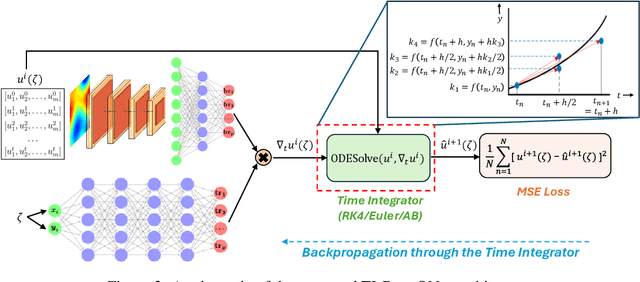
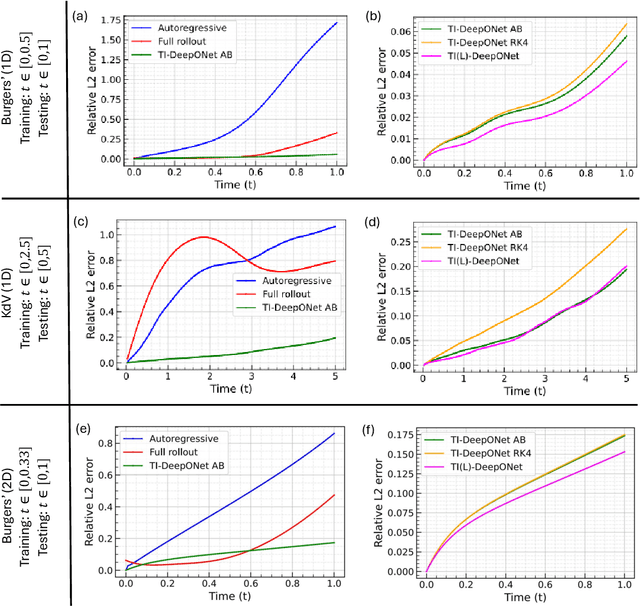
Accurate temporal extrapolation presents a fundamental challenge for neural operators in modeling dynamical systems, where reliable predictions must extend significantly beyond the training time horizon. Conventional Deep Operator Network (DeepONet) approaches employ two inherently limited training paradigms - fixed-horizon rollouts that predict complete spatiotemporal solutions while disregarding temporal causality, and autoregressive formulations that accumulate errors through sequential predictions. We introduce TI-DeepONet, a framework that integrates neural operators with adaptive numerical time-stepping techniques to preserve the Markovian structure of dynamical systems while mitigating error propagation in extended temporal forecasting. Our approach reformulates the learning objective from direct state prediction to the approximation of instantaneous time-derivative fields, which are then integrated using established numerical schemes. This architecture supports continuous-time prediction and enables deployment of higher-precision integrators during inference than those used during training, balancing computational efficiency with predictive accuracy. We further develop TI(L)-DeepONet, which incorporates learnable coefficients for intermediate slopes in the integration process, adapting to solution-specific variations and enhancing fidelity. Evaluation across three canonical PDEs shows that TI(L)-DeepONet marginally outperforms TI-DeepONet, with both reducing relative L2 extrapolation errors: approximately 81% over autoregressive and 70% over fixed-horizon methods. Notably, both maintain prediction stability for temporal domains extending to about twice the training interval. This research establishes a physics-aware operator learning paradigm that bridges neural approximation with numerical analysis while preserving the causal structure of dynamical systems.

Enabling Local Neural Operators to perform Equation-Free System-Level Analysis

Neural Operators (NOs) provide a powerful framework for computations involving physical laws that can be modelled by (integro-) partial differential equations (PDEs), directly learning maps between infinite-dimensional function spaces that bypass both the explicit equation identification and their subsequent numerical solving. Still, NOs have so far primarily been employed to explore the dynamical behavior as surrogates of brute-force temporal simulations/predictions. Their potential for systematic rigorous numerical system-level tasks, such as fixed-point, stability, and bifurcation analysis - crucial for predicting irreversible transitions in real-world phenomena - remains largely unexplored. Toward this aim, inspired by the Equation-Free multiscale framework, we propose and implement a framework that integrates (local) NOs with advanced iterative numerical methods in the Krylov subspace, so as to perform efficient system-level stability and bifurcation analysis of large-scale dynamical systems. Beyond fixed point, stability, and bifurcation analysis enabled by local in time NOs, we also demonstrate the usefulness of local in space as well as in space-time ("patch") NOs in accelerating the computer-aided analysis of spatiotemporal dynamics. We illustrate our framework via three nonlinear PDE benchmarks: the 1D Allen-Cahn equation, which undergoes multiple concatenated pitchfork bifurcations; the Liouville-Bratu-Gelfand PDE, which features a saddle-node tipping point; and the FitzHugh-Nagumo (FHN) model, consisting of two coupled PDEs that exhibit both Hopf and saddle-node bifurcations.

Accelerating Multiscale Modeling with Hybrid Solvers: Coupling FEM and Neural Operators with Domain Decomposition

Numerical solvers for partial differential equations (PDEs) face challenges balancing computational cost and accuracy, especially in multiscale and dynamic systems. Neural operators can significantly speed up simulations; however, they often face challenges such as error accumulation and limited generalization in multiphysics problems. This work introduces a novel hybrid framework that integrates physics-informed DeepONet with FEM through domain decomposition. The core innovation lies in adaptively coupling FEM and DeepONet subdomains via a Schwarz alternating method. This methodology strategically allocates computationally demanding regions to a pre-trained Deep Operator Network, while the remaining computational domain is solved through FEM. To address dynamic systems, we integrate the Newmark time-stepping scheme directly into the DeepONet, significantly mitigating error accumulation in long-term simulations. Furthermore, an adaptive subdomain evolution enables the ML-resolved region to expand dynamically, capturing emerging fine-scale features without remeshing. The framework's efficacy has been validated across a range of solid mechanics problems, including static, quasi-static, and dynamic regimes, demonstrating accelerated convergence rates (up to 20% improvement compared to FE-FE approaches), while preserving solution fidelity with error < 1%. Our case studies show that our proposed hybrid solver: (1) maintains solution continuity across subdomain interfaces, (2) reduces computational costs by eliminating fine mesh requirements, (3) mitigates error accumulation in time-dependent simulations, and (4) enables automatic adaptation to evolving physical phenomena. This work bridges the gap between numerical methods and AI-driven surrogates, offering a scalable pathway for high-fidelity simulations in engineering and scientific applications.

Physics-Informed Latent Neural Operator for Real-time Predictions of Complex Physical Systems

Deep operator network (DeepONet) has shown great promise as a surrogate model for systems governed by partial differential equations (PDEs), learning mappings between infinite-dimensional function spaces with high accuracy. However, achieving low generalization errors often requires highly overparameterized networks, posing significant challenges for large-scale, complex systems. To address these challenges, latent DeepONet was proposed, introducing a two-step approach: first, a reduced-order model is used to learn a low-dimensional latent space, followed by operator learning on this latent space. While effective, this method is inherently data-driven, relying on large datasets and making it difficult to incorporate governing physics into the framework. Additionally, the decoupled nature of these steps prevents end-to-end optimization and the ability to handle data scarcity. This work introduces PI-Latent-NO, a physics-informed latent operator learning framework that overcomes these limitations. Our architecture employs two coupled DeepONets in an end-to-end training scheme: the first, termed Latent-DeepONet, identifies and learns the low-dimensional latent space, while the second, Reconstruction-DeepONet, maps the latent representations back to the original physical space. By integrating governing physics directly into the training process, our approach requires significantly fewer data samples while achieving high accuracy. Furthermore, the framework is computationally and memory efficient, exhibiting nearly constant scaling behavior on a single GPU and demonstrating the potential for further efficiency gains with distributed training. We validate the proposed method on high-dimensional parametric PDEs, demonstrating its effectiveness as a proof of concept and its potential scalability for large-scale systems.

Learning Hidden Physics and System Parameters with Deep Operator Networks

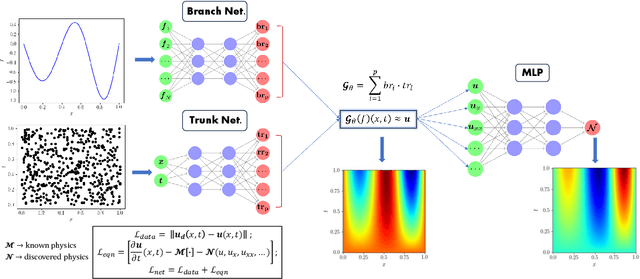
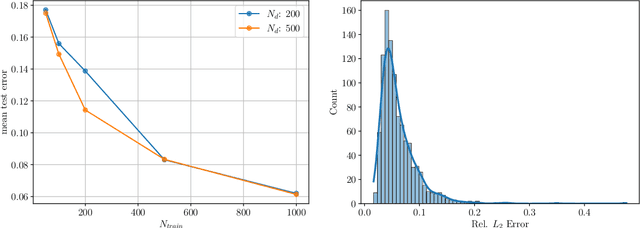
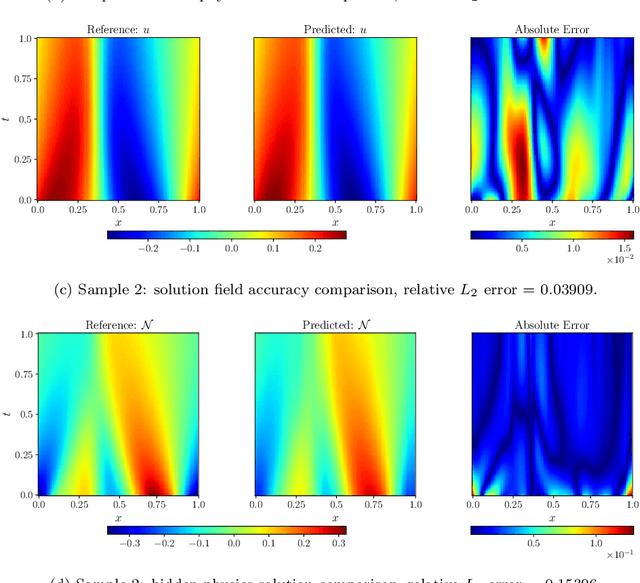
Big data is transforming scientific progress by enabling the discovery of novel models, enhancing existing frameworks, and facilitating precise uncertainty quantification, while advancements in scientific machine learning complement this by providing powerful tools to solve inverse problems to identify the complex systems where traditional methods falter due to sparse or noisy data. We introduce two innovative neural operator frameworks tailored for discovering hidden physics and identifying unknown system parameters from sparse measurements. The first framework integrates a popular neural operator, DeepONet, and a physics-informed neural network to capture the relationship between sparse data and the underlying physics, enabling the accurate discovery of a family of governing equations. The second framework focuses on system parameter identification, leveraging a DeepONet pre-trained on sparse sensor measurements to initialize a physics-constrained inverse model. Both frameworks excel in handling limited data and preserving physical consistency. Benchmarking on the Burgers' equation and reaction-diffusion system demonstrates state-of-the-art performance, achieving average $L_2$ errors of $\mathcal{O}(10^{-2})$ for hidden physics discovery and absolute errors of $\mathcal{O}(10^{-3})$ for parameter identification. These results underscore the frameworks' robustness, efficiency, and potential for solving complex scientific problems with minimal observational data.

Synergistic Learning with Multi-Task DeepONet for Efficient PDE Problem Solving

Multi-task learning (MTL) is an inductive transfer mechanism designed to leverage useful information from multiple tasks to improve generalization performance compared to single-task learning. It has been extensively explored in traditional machine learning to address issues such as data sparsity and overfitting in neural networks. In this work, we apply MTL to problems in science and engineering governed by partial differential equations (PDEs). However, implementing MTL in this context is complex, as it requires task-specific modifications to accommodate various scenarios representing different physical processes. To this end, we present a multi-task deep operator network (MT-DeepONet) to learn solutions across various functional forms of source terms in a PDE and multiple geometries in a single concurrent training session. We introduce modifications in the branch network of the vanilla DeepONet to account for various functional forms of a parameterized coefficient in a PDE. Additionally, we handle parameterized geometries by introducing a binary mask in the branch network and incorporating it into the loss term to improve convergence and generalization to new geometry tasks. Our approach is demonstrated on three benchmark problems: (1) learning different functional forms of the source term in the Fisher equation; (2) learning multiple geometries in a 2D Darcy Flow problem and showcasing better transfer learning capabilities to new geometries; and (3) learning 3D parameterized geometries for a heat transfer problem and demonstrate the ability to predict on new but similar geometries. Our MT-DeepONet framework offers a novel approach to solving PDE problems in engineering and science under a unified umbrella based on synergistic learning that reduces the overall training cost for neural operators.

Separable DeepONet: Breaking the Curse of Dimensionality in Physics-Informed Machine Learning

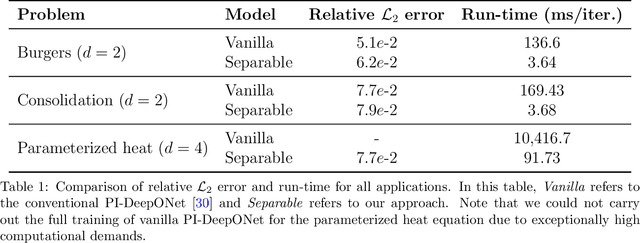
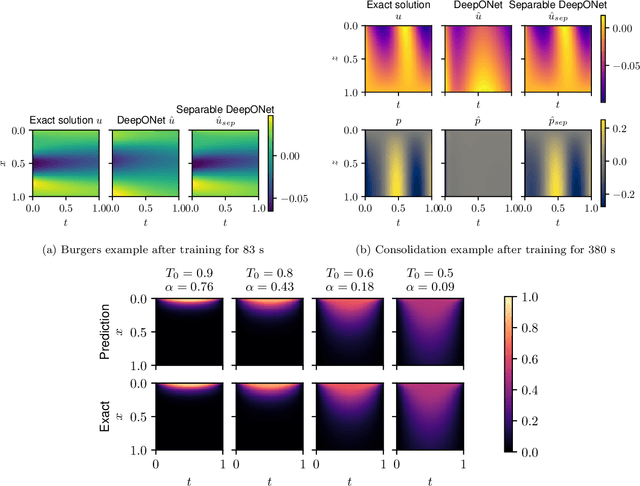
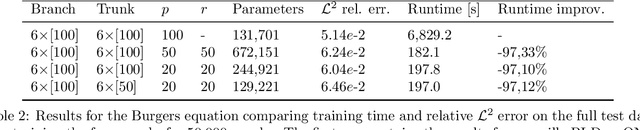
The deep operator network (DeepONet) is a popular neural operator architecture that has shown promise in solving partial differential equations (PDEs) by using deep neural networks to map between infinite-dimensional function spaces. In the absence of labeled datasets, we utilize the PDE residual loss to learn the physical system, an approach known as physics-informed DeepONet. This method faces significant computational challenges, primarily due to the curse of dimensionality, as the computational cost increases exponentially with finer discretization. In this paper, we introduce the Separable DeepONet framework to address these challenges and improve scalability for high-dimensional PDEs. Our approach involves a factorization technique where sub-networks handle individual one-dimensional coordinates, thereby reducing the number of forward passes and the size of the Jacobian matrix. By using forward-mode automatic differentiation, we further optimize the computational cost related to the Jacobian matrix. As a result, our modifications lead to a linear scaling of computational cost with discretization density, making Separable DeepONet suitable for high-dimensional PDEs. We validate the effectiveness of the separable architecture through three benchmark PDE models: the viscous Burgers equation, Biot's consolidation theory, and a parametrized heat equation. In all cases, our proposed framework achieves comparable or improved accuracy while significantly reducing computational time compared to conventional DeepONet. These results demonstrate the potential of Separable DeepONet in efficiently solving complex, high-dimensional PDEs, advancing the field of physics-informed machine learning.