Recency-Weighted Temporally-Segmented Ensemble for Time-Series Modeling

Time-series modeling in process industries faces the challenge of dealing with complex, multi-faceted, and evolving data characteristics. Conventional single model approaches often struggle to capture the interplay of diverse dynamics, resulting in suboptimal forecasts. Addressing this, we introduce the Recency-Weighted Temporally-Segmented (ReWTS, pronounced `roots') ensemble model, a novel chunk-based approach for multi-step forecasting. The key characteristics of the ReWTS model are twofold: 1) It facilitates specialization of models into different dynamics by segmenting the training data into `chunks' of data and training one model per chunk. 2) During inference, an optimization procedure assesses each model on the recent past and selects the active models, such that the appropriate mixture of previously learned dynamics can be recalled to forecast the future. This method not only captures the nuances of each period, but also adapts more effectively to changes over time compared to conventional `global' models trained on all data in one go. We present a comparative analysis, utilizing two years of data from a wastewater treatment plant and a drinking water treatment plant in Norway, demonstrating the ReWTS ensemble's superiority. It consistently outperforms the global model in terms of mean squared forecasting error across various model architectures by 10-70\% on both datasets, notably exhibiting greater resilience to outliers. This approach shows promise in developing automatic, adaptable forecasting models for decision-making and control systems in process industries and other complex systems.

Road Graph Generator: Mapping roads at construction sites from GPS data

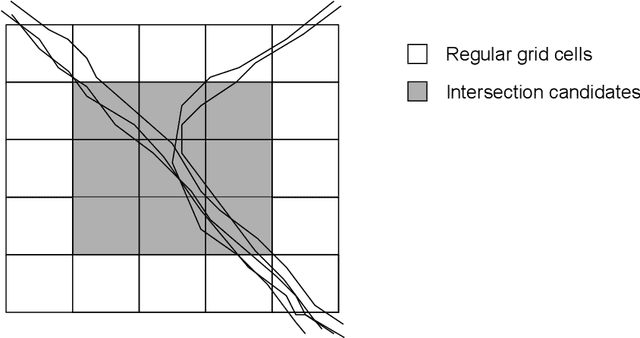
We present a method for road inference from GPS trajectories to map construction sites. This task introduces a unique challenge due to the erratic and non-standard movement patterns of construction machinery, which diverge significantly from typical vehicular traffic on established roads. Our method first identifies intersections in the road network that serve as critical decision points, and later connects them with edges, producing a graph, which subsequently can be used for planning and task-allocation. We demonstrate the effectiveness of our approach by mapping roads at a real-life construction site in Norway.

DON-LSTM: Multi-Resolution Learning with DeepONets and Long Short-Term Memory Neural Networks

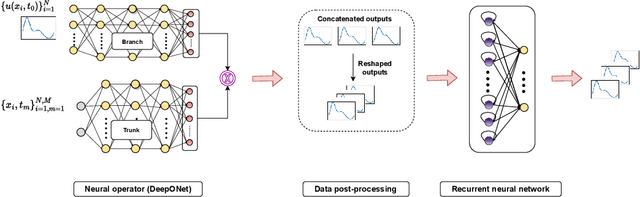
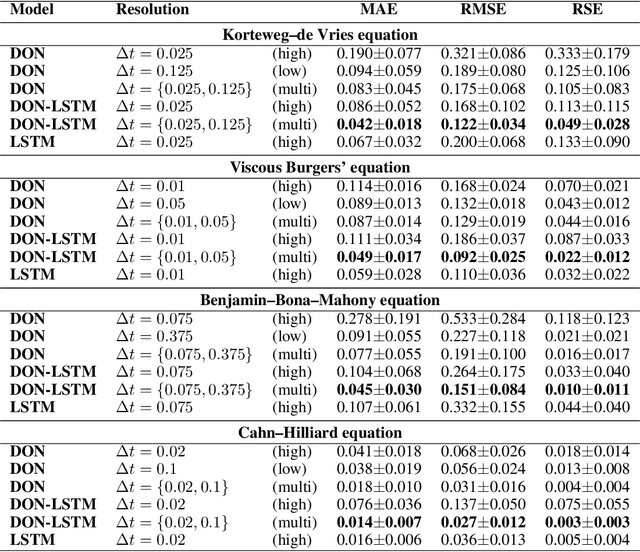
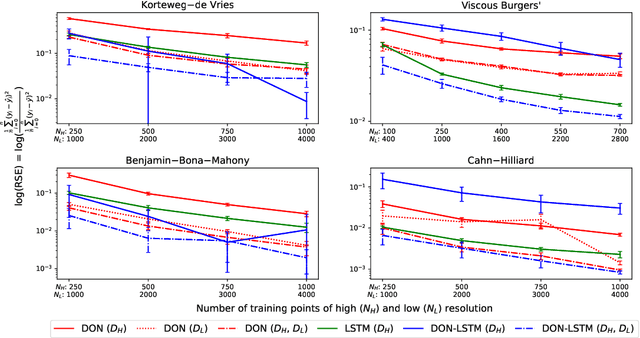
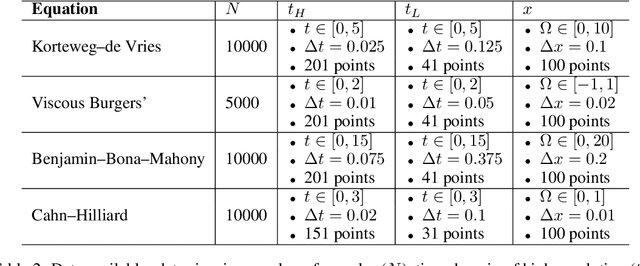
Deep operator networks (DeepONets, DONs) offer a distinct advantage over traditional neural networks in their ability to be trained on multi-resolution data. This property becomes especially relevant in real-world scenarios where high-resolution measurements are difficult to obtain, while low-resolution data is more readily available. Nevertheless, DeepONets alone often struggle to capture and maintain dependencies over long sequences compared to other state-of-the-art algorithms. We propose a novel architecture, named DON-LSTM, which extends the DeepONet with a long short-term memory network (LSTM). Combining these two architectures, we equip the network with explicit mechanisms to leverage multi-resolution data, as well as capture temporal dependencies in long sequences. We test our method on long-time-evolution modeling of multiple non-linear systems and show that the proposed multi-resolution DON-LSTM achieves significantly lower generalization error and requires fewer high-resolution samples compared to its vanilla counterparts.

Pseudo-Hamiltonian system identification

Identifying the underlying dynamics of physical systems can be challenging when only provided with observational data. In this work, we consider systems that can be modelled as first-order ordinary differential equations. By assuming a certain pseudo-Hamiltonian formulation, we are able to learn the analytic terms of internal dynamics even if the model is trained on data where the system is affected by unknown damping and external disturbances. In cases where it is difficult to find analytic terms for the disturbances, a hybrid model that uses a neural network to learn these can still accurately identify the dynamics of the system as if under ideal conditions. This makes the models applicable in situations where other system identification models fail. Furthermore, we propose to use a fourth-order symmetric integration scheme in the loss function and avoid actual integration in the training, and demonstrate on varied examples how this leads to increased performance on noisy data.

Neural Operator Learning for Long-Time Integration in Dynamical Systems with Recurrent Neural Networks

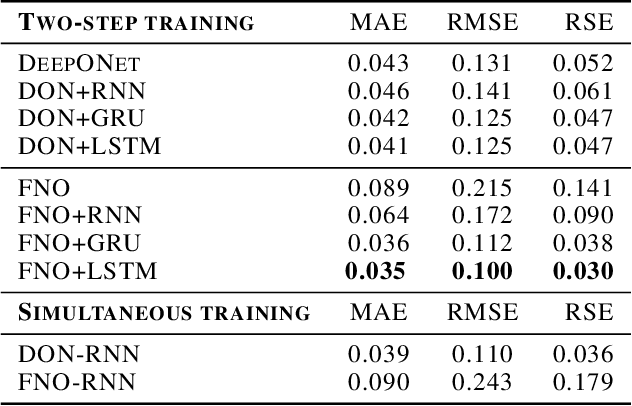
Deep neural networks are an attractive alternative for simulating complex dynamical systems, as in comparison to traditional scientific computing methods, they offer reduced computational costs during inference and can be trained directly from observational data. Existing methods, however, cannot extrapolate accurately and are prone to error accumulation in long-time integration. Herein, we address this issue by combining neural operators with recurrent neural networks to construct a novel and effective architecture, resulting in superior accuracy compared to the state-of-the-art. The new hybrid model is based on operator learning while offering a recurrent structure to capture temporal dependencies. The integrated framework is shown to stabilize the solution and reduce error accumulation for both interpolation and extrapolation of the Korteweg-de Vries equation.

Port-Hamiltonian Neural Networks with State Dependent Ports

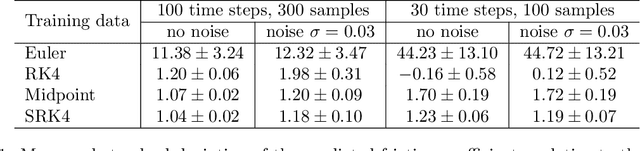
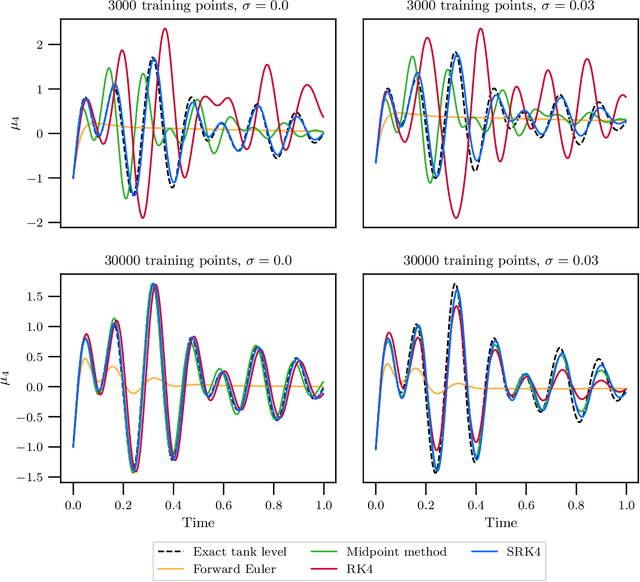
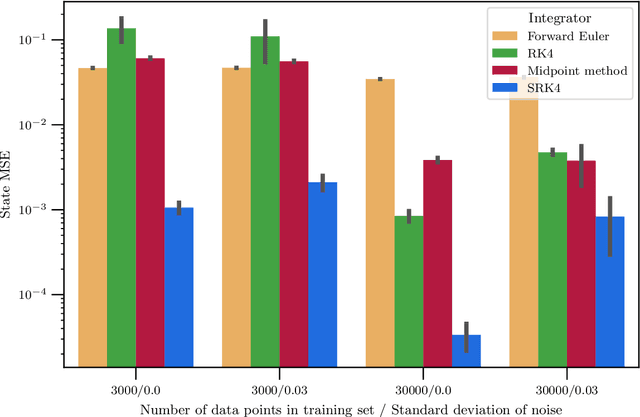
Hybrid machine learning based on Hamiltonian formulations has recently been successfully demonstrated for simple mechanical systems. In this work, we stress-test the method on both simple mass-spring systems and more complex and realistic systems with several internal and external forces, including a system with multiple connected tanks. We quantify performance under various conditions and show that imposing different assumptions greatly affect the performance during training presenting advantages and limitations of the method. We demonstrate that port-Hamiltonian neural networks can be extended to larger dimensions with state-dependent ports. We consider learning on systems with known and unknown external forces and show how it can be used to detect deviations in a system and still provide a valid model when the deviations are removed. Finally, we propose a symmetric high-order integrator for improved training on sparse and noisy data.

Mutual information estimation for graph convolutional neural networks

Measuring model performance is a key issue for deep learning practitioners. However, we often lack the ability to explain why a specific architecture attains superior predictive accuracy for a given data set. Often, validation accuracy is used as a performance heuristic quantifying how well a network generalizes to unseen data, but it does not capture anything about the information flow in the model. Mutual information can be used as a measure of the quality of internal representations in deep learning models, and the information plane may provide insights into whether the model exploits the available information in the data. The information plane has previously been explored for fully connected neural networks and convolutional architectures. We present an architecture-agnostic method for tracking a network's internal representations during training, which are then used to create the mutual information plane. The method is exemplified for graph-based neural networks fitted on citation data. We compare how the inductive bias introduced in graph-based architectures changes the mutual information plane relative to a fully connected neural network.

Inferring feature importance with uncertainties in high-dimensional data

Estimating feature importance is a significant aspect of explaining data-based models. Besides explaining the model itself, an equally relevant question is which features are important in the underlying data generating process. We present a Shapley value based framework for inferring the importance of individual features, including uncertainty in the estimator. We build upon the recently published feature importance measure of SAGE (Shapley additive global importance) and introduce sub-SAGE which can be estimated without resampling for tree-based models. We argue that the uncertainties can be estimated from bootstrapping and demonstrate the approach for tree ensemble methods. The framework is exemplified on synthetic data as well as high-dimensional genomics data.

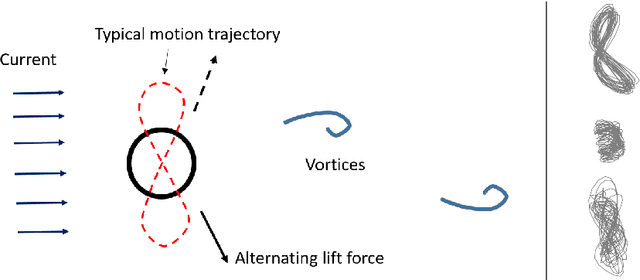
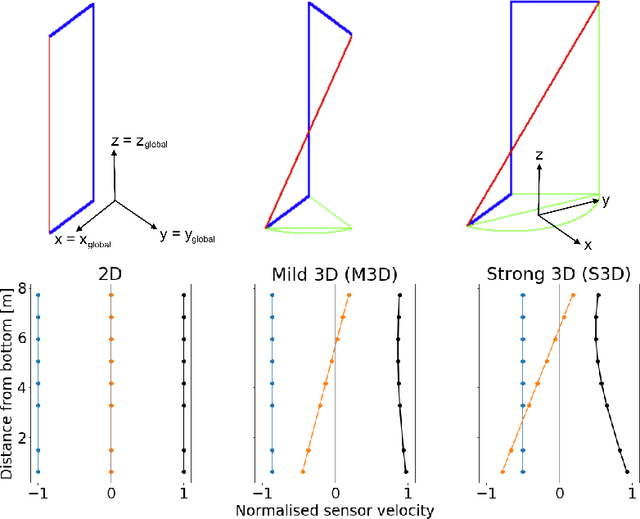
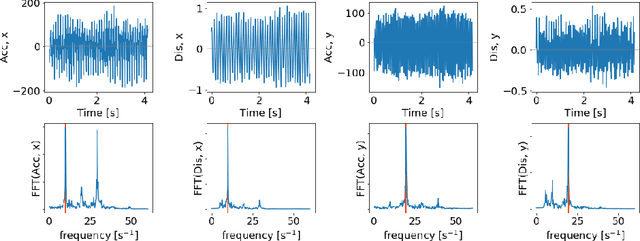
Data-driven prediction of vortex-induced vibration response of marine risers subjected to three-dimensional current

Slender marine structures such as deep-water marine risers are subjected to currents and will normally experience Vortex Induced Vibrations (VIV), which can cause fast accumulation of fatigue damage. The ocean current is often three-dimensional (3D), i.e., the direction and magnitude of the current vary throughout the water column. Today, semi-empirical tools are used by the industry to predict VIV induced fatigue on risers. The load model and hydrodynamic parameters in present VIV prediction tools are developed based on two-dimensional (2D) flow conditions, as it is challenging to consider the effect of 3D flow along the risers. Accordingly, the current profiles must be purposely made 2D during the design process, which leads to significant uncertainty in the prediction results. Further, due to the limitations in the laboratory, VIV model tests are mostly carried out under 2D flow conditions and thus little experimental data exist to document VIV response of riser subjected to varying directions of the current. However, a few experiments have been conducted with 3D current. We have used results from one of these experiments to investigate how well 1) traditional and 2) an alternative method based on a data driven prediction can describe VIV in 3D currents. Data driven modelling is particularly suited for complicated problems with many parameters and non-linear relationships. We have applied a data clustering algorithm to the experimental 3D flow data in order to identify measurable parameters that can influence responses. The riser responses are grouped based on their statistical characteristics, which relate to the direction of the flow. Furthermore we fit a random forest regression model to the measured VIV response and compare its performance with the predictions of existing VIV prediction tools (VIVANA-FD).