Neural Operator Learning for Long-Time Integration in Dynamical Systems with Recurrent Neural Networks

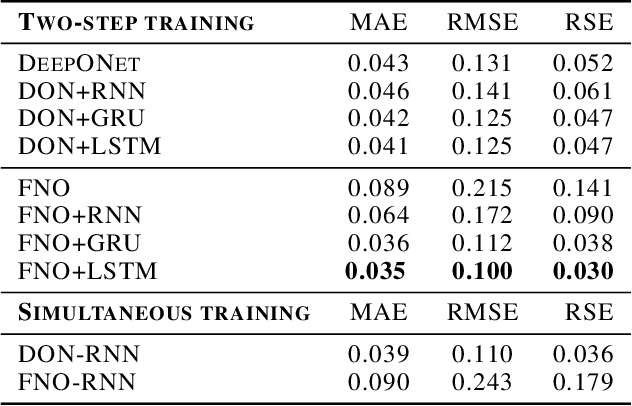
Deep neural networks are an attractive alternative for simulating complex dynamical systems, as in comparison to traditional scientific computing methods, they offer reduced computational costs during inference and can be trained directly from observational data. Existing methods, however, cannot extrapolate accurately and are prone to error accumulation in long-time integration. Herein, we address this issue by combining neural operators with recurrent neural networks to construct a novel and effective architecture, resulting in superior accuracy compared to the state-of-the-art. The new hybrid model is based on operator learning while offering a recurrent structure to capture temporal dependencies. The integrated framework is shown to stabilize the solution and reduce error accumulation for both interpolation and extrapolation of the Korteweg-de Vries equation.